EMD自相关阈值去噪法在水电机组振动信号中的研究

徐艳春，方绍晨

(梯级水电站运行与控制湖北省重点实验室(三峡大学), 湖北 宜昌 443002)

0 引 言

随着水电产业的快速发展，大规模的水电机组并网运行，水电机组的稳定运行关系着电网的安全与稳定。据相关文献显示，80%的水电机组故障都与振动有关[1]，对水电机组进行振动信号的提取是水电机组状态监测和故障诊断的重要一步。由于现场环境的干扰，在实际的水电机组振动信号监测提取中往往会取得混有噪声的振动信号，为了准确反映水电机组的运行情况，需要对所提取的振动信号进行去噪处理。

针对水电机组振动信号去噪，目前主要采用的是以小波分析为主的去噪方法，例如利用改进的小波阈值去噪法[2]，基于多小波的水电机组振动信号降噪[3]，都取得了一定的效果。经验模态分解(EMD)是一种自适应数据处理方法，适合非线性、非平稳的时间序列的处理，它能将信号分解成若干个固有模态函数(IMF)，IMF分量分别表征了原始信号高频到低频的含量，在去噪领域的应用中，认为高频部分的IMF包含了大量的噪声信号，而低频部分则表征原始信号的趋势或者均值。因此，这种将提取信号分解成IMF分量的方法能够有效去除噪声[4]，得到信号的趋势量。EMD去噪已经在图像去噪[5]以及光谱的去噪中[6]得到了应用。鉴于在水电机组出现故障时，振动时变信号的非平稳性和复杂性会更加突出，而小波分析以及EMD存在各自的缺点，以及面对短时噪声干扰的局限性，本文将小波阈值法和经验模态分解法相结合，并将这种EMD相关阈值去噪法用于水电机组振动信号的去噪中，取得了良好的效果。

1 EMD基本原理

经验模态分解(EMD Empirical Mode Decomposition)是Huang提出的一种信号分解算法，这种算法认为任何信号都可以分解成若干个固有模态函数(IMF),这些IMF分量含有不同时间尺度下的原始信号的特征，这些分量具有如下特征。①整个信号的极值点和过零点数量最多不大于1;②信号任意点处通过极大值和极小值确定的上下包络线均值为0。

经验模态分解的具体步骤如下：

(1)确定信号s(t)所有的极大值点和极小值点，然后将所有极大值点和所有极小值点分别用一条光滑的曲线连接起来，使两条曲线间包含所有的信号。上下包络线的平均值记为m1(t):

s(t)-m1(t)=h1(t)

(1)

如果h1(t)是一个固有模态分量，那么h1(t)就是s(t)的第一个分量。

(2)一般情况下h1(t)不满足固有模态函数的条件，因此把h1(t)作为原始数据，重复步骤(1)，反复筛选k次，得到：

h1k=h1(k-1)-m1k(t)

(2)

使得h1k(t)成为一个IMF分量。记c1(t)=h1k(t)，则将c1(t)作为原始信号s(t)的第一个IMF分量。

(3)c1(t)中应该包含信号中最短或者最精细的分量，将c1(t)从信号中分离出来得：

r1(t)=s(t)-c1(t)

(3)

将r1(t)作为原始数据重复步骤(1)(2)，得到s(t)的第二个满足条件的IMF分量c2(t)。重复循环n次后得到n个s(t)的IMF分量。

(4)

整个过程遇到如下任何一个条件就停止，①当分量cn(t)或者残量rn(t)足够小；②当残量为一个不能从中提取出固有模态函数的单调函数时。这样就由式(2)、(4)得到：

(5)

这样，就可以把任何一个信号分解成n个固有模态分量和一个残量的和，c1(t),c2(t),…,cn(t)分别表示了信号由高频到低频的部分，且随着信号本身的变化而变化。由此可以看出，经验模态分解法具备包括自适应性、正交性和完备性在内的长处[7]。通常在利用EMD法做降噪处理时，往往将最高频的IMF分量作为噪声部分直接去除，这样简单利用EMD作为去噪方法去噪效果有限，同时也可能去除有用的信号。EMD分解将原始信号分解为频率由高到低的IMF分量，且分量之间的频率特征明显，这体现了EMD分解的自适应性，可以利用EMD方法的这一特性，对分解出的各频段的IMF进行对应的处理，以此作为更好地去噪手段。

2 自相关能量准则及其在EMD中的应用

为了表现函数在不同时间点的相似程度，构建了自相关函数，表示为：

(6)

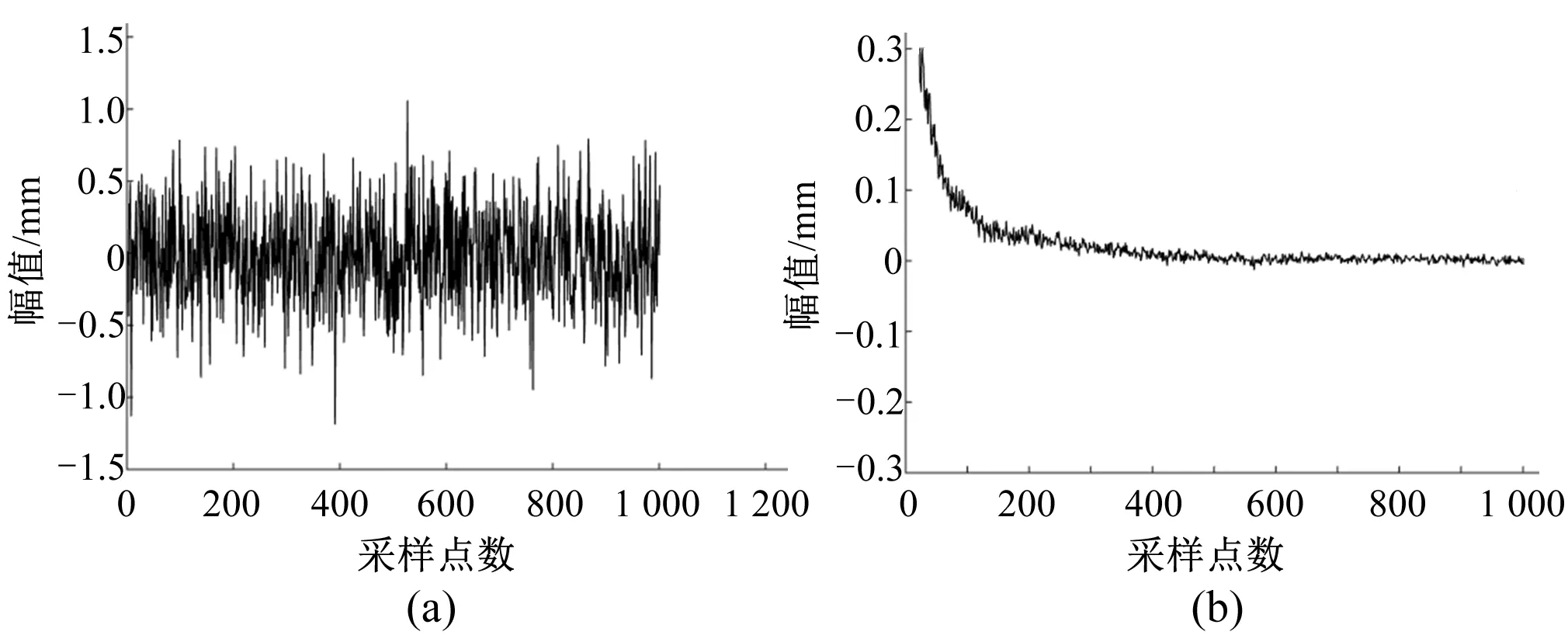
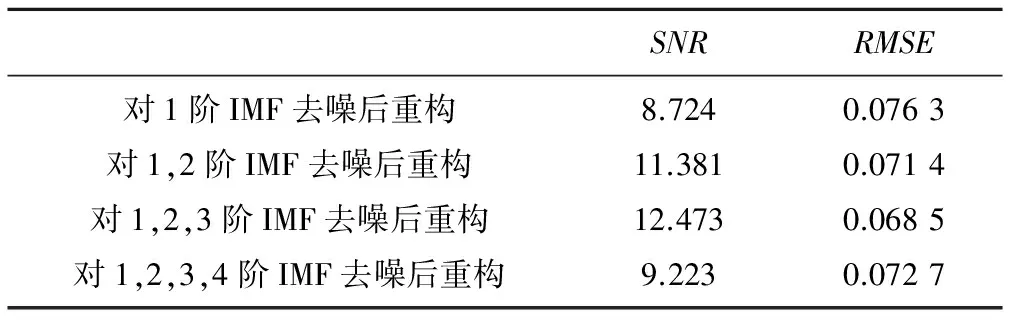
式中：m表示时延；N表示信号长度，满足0

图1是含有3个正弦信号的普通信号和由式(6)计算得出的自相关函数序列，图2是噪声信号和对应的自相关函数序列部分图形。从图中可以看出随机信号和普通信号的自相关函数分布特点，可以看出由于随机噪声各个时刻关联性弱且随机性强，它的自相关函数在零点取得最大然后迅速衰减，在其他点处自相关函数值迅速衰减到很小。以正弦信号为代表的普通信号在不同时刻有着较强的关联性，其自相关函数并没有迅速衰减而是保持震荡。

图1 普通信号及其自相关函数Fig.1Common signal and its autocorrelation function

图2 噪声信号及其自相关函数Fig.2 Noise signal and its autocorrelation function (right)

信号能量准则计算公式为：

(7)

式中：τ为远小于N的常数，保证所计算的随机信号自相关函数能量是衰减之后的，使得计算结果区别于普通信号。表1是选取相近能量的随机信号和一般信号的自相关函数能量对比。可以看出，随机信号自相关函数的能量要远低于一般信号，因此可以用这一特性作为对噪声的识别依据。

表1 信号和其自相关函数的能量对比Tab.1 Energy contrast of signal and its autocorrelation function

EMD分解法将原始信号分解成若干从高频到低频分布的IMF分量，在传统信号去噪领域，往往将高频分量作为噪声部分，但是对于高频分量的选择并没有一个统一的标准，鉴于自相关函数能量准则可以有效识别随机信号和一般信号，因而可以将IMF分量中自相关函数能量值明显小于其他分量的部分作为含有噪声最多的IMF分量，进而对所选分量进行处理，来达到去噪目的。

3 小波阈值去噪

小波阈值去噪的基本原理是先将原始信号进行小波分解，通过设定阈值，对分解后各层系数进行处理，按照阈值函数，将系数模大于阈值或者小于阈值的部分分别用不同的方式进行修改，最后重构各分量获得最终信号。去噪过程分为3个步骤：

(1)确定小波和需要分解的层数n进行分解;

(2)根据每层小波系数选择阈值，并按照阈值函数对小波高频系数进行处理；

(3)重构处理后的各层小波分量得到最终信号。

其中阈值的选择主要有固定阈值形式、基于史坦的无偏似然估计原理的自适应阈值、启发式阈值[8]。

传统的阈值函数分为硬阈值函数和软阈值函数，其中硬阈值函数把小波系数小于阈值的部分设为0，大于阈值的部分不变。而软阈值函数把大于阈值的部分设为原系数与阈值之差，小于阈值的部分设为0。

硬阈值函数：

(8)

软阈值函数：

(9)

从软、硬阈值函数的定义可知，它们优点是算法简单，且都有一定的去噪能力;但是它们的缺点也很明显。软阈值函数在小波系数大于阈值时，其估计出的信号与原始信号之间存在着恒定的偏差，这必影响到重构信号的精度;而硬阈值函数处理过的信号在阈值处是间断的，重构时易产生局部的附加振荡，使得重构后的信号不会同原始信号一样的光滑。为了同时克服软、硬阈值函数的缺点[9]，以及对EMD分解的适应性，本文提出了一种改进的阈值函数，考虑到不同阶数IMF分量的噪声含量不同，在阈值函数中引入了当前阈值去噪所处理的IMF阶数G(s)，以及调节参数a,b。其函数表达式如下:

(10)

4 仿真实例

4.1 仿真信号的构建

水电机组振动频率和机组故障原因以及参数有关[10]，可以以此作为构建仿真信号的依据。

某水电机组参数与故障成因以及频率计算方式如表2及表3所示。

表2 某水电站机组参数Tab.2 Parameters of a hydropower station

表3 水电机组故障原因及频率成分关系Tab.3 Relationship between fault causes and frequency components of hydroelectric generating units

表3给出了水电机组水力、机械、电气3个方面故障原因所引起的机组振动的振动信号频率成分，据此可以构造该机组含有噪声时的振动仿真信号：

s(t)=f(t)+z(t)=

0.33 sin(1.62πt)+0.19sin(3.57πt)+0.12sin(17.85πt)+

0.1sin(42.8πt)+0.11sin(85.68πt)+0.15sin(200πt)+z(t)

式中：f(t)是有效振动信号；z(t)为添加的高斯白噪声信号。

4.2 仿真信号去噪

EMD相关阈值去噪法流程图如图3所示。

图3 EMD相关阈值去噪法流程Fig.3 EMD autocorrelation wavelet threshold denoising

由表2及表3构建的振动仿真信号和染噪信号如图4所示，所添加的白噪声SNR为8。

图4 有效振动信号及其染噪信号Fig.4 Effective vibration signal and its noise signal

对染噪信号s(t)进行EMD分解，分解后的7层IMF如图5所示,对应的自相关函数曲线如图6。

图5 染噪信号EMD分解7阶IMF分量Fig.5 Seven-order IMF of EMD for the signal with noise

图6 7阶IMF分量的自相关函数曲线Fig.6 Autocorrelation function of Seven-order IMF

E(1)E(2)E(3)E(4)E(5)E(6)E(7)0．00530．00170．00130．07640．77970．03100．1184

图7 IMF分量的自相关函数能量Fig.7 Autocorrelation function energy of IMF

图8 去噪重构信号和有效振动信号Fig.8 Denoising reconstruction signal and effective vibration signal

表4为每一阶IMF分量的自相关函数能量，图7是自相关能量大小随阶数变化的曲线，可以看出1,2,3阶IMF分量的能量显著小于其他各阶，因此选取前3阶作为噪声主导的分量，并用式(7)所示阈值函数对它们进行小波阈值去噪，去噪后的重构信号和无噪的原始信号如图8所示。通过计算去噪信号的信噪比(SNR)和均方根误差(RMSE)作为衡量去噪效果的依据,SNR和RMSE的计算公式如下：

(12)

为了比较对各阶IMF分量去噪后重构所得到的去噪信号效果，分别做了对1阶，1,2阶，1,2,3,4阶IMF去噪后重构的实验作为对照，结果如表5所示。

表5 各种情况下信噪比及其均方根误差Tab. 5 Signal to noise ratio and its root mean square error in various situations

从实验结果可以看出，对前3阶IMF分量进行小波阈值去噪后重构，所得到的振动信号无论是在信噪 比还是在均方根误差上的表现上都更好。

5 结 语

EMD相关阈值去噪法理论基础可靠，利用自相关能量准则将EMD算法和小波阈值去噪法有效结合在一起，通过比较自相关函数能量选取高频IMF分量作为小波阈值去噪的对象，这种方法避免了小波阈值法作用于整个信号所可能带来的误差，仿真实验证明了自相关能量准则能够准确选择出用于小波阈值处理的IMF分量，也证明了EMD相关阈值去噪法能够有效降低振动信号中的噪声，突出振动信号中隐含的故障信息，可以有效用于水电机组振动信号的去噪中。

□

[1] 沈 东,褚福涛,陈 思.水轮发电机组振动故障诊断与识别[J].水动力研究与进展,2000,15(1): 129-133.

[2] 安周鹏,肖志怀,孙召辉,等.改进小波阈值降噪算法在水电机组信号处理中的应用[J].中国农村水利水电,2014,(12):165-169.

[3] 张广涛,宋丽波,张晓静,等.基于多小波的水电机组振动信号降噪方法研究[J].中国农村水利水电.2016,(5):163-170.

[4] 高云超,桑恩方,刘百峰.基于经验模式分解的自适应去噪算法[J].计算机工程与应用,2007,(27):59-61.

[5] 郭 耸,顾国昌,李常有,等.利用EMD的自适应图像去噪[J].计算机工程与应用，2013,49(8):12-16.

[6] 李 卿,张国平,刘 洋.基于EMD的拉曼光谱去噪方法研究[J].光谱学与光谱分析,2009,29(1):142-145.

[7] 宁 静.基于EMD和Cohen核的时提顷分析研究及其在轨道不平顺监测中的应用[D].成都:西南交通大学,2002.

[8] 刘卫东,刘尚介,胡小锋,等.小波阈值去噪函数的改进方法分析[J].高电压技术,2007,33(10):59-63.

[9] 叶重元,黄永东.小波阈值去噪算法的新改进[J].计算机工程与应用,2011,47(12):141-148.

[10] 赵道利,梁武利,罗兴锜,等.水电机组振动信号的子带能量特征提取方法研究[J].水力发电学报,2004,23(6):116-119.