基于LWCA-SVM模型对洪泽湖饮用水源地二河闸断面水质的预测分析
2017-03-22戴青松王沛芳刘佳佳
戴青松,王沛芳,王 超,姚 羽,俞 阳,刘佳佳,侯 俊
(1.河海大学环境学院,南京 210098;2.河海大学浅水湖泊综合治理与资源开发教育部重点实验室,南京 210098)
0 引 言
随着经济的发展和人口的快速增长,我国的河流湖泊受到不同程度的污染[1],湖泊富营养化发展速度加快。污染物来源复杂、危害大、处理困难,导致了水源地水质恶化难以处理,严重威胁着饮用水供水安全[2,3]。二河位于洪泽湖东边,是淮安市重要的河流型水源地[4]。二河闸位于二河流域上游,是洪泽湖出湖的主要控制工程之一,其总氮(TN)、总磷(TP)作为富营养化的重要指标近年来均出现了超标情况,同时溶解氧(DO)作为指示河流污染程度的指标之一波动幅度较大,不利于水生生物的生长繁殖,因此对二河闸TN、TP和DO指标的准确预测对水源地水质管理和规划管理十分重要。
水质预测模型主要有两类[5,6],一类是水质机理预测模型,另一类是数据驱动水质预测模型。神经网络模型和支持向量机模型是当前主要研究的数据驱动预测模型。研究发现,支持向量机模型,具有模型计算简单、推广适应能力强等优点[1,7]。刘双印等人[8]在养殖水质预测中,利用了主成分分析、改进文化鱼群算法和最小二乘支持向量机模型,得到的相对误差小于8%。程庭莉[9]将差分自回归移动平均模型和支持向量机结合使用,并且采用变种群的自适应遗传算法优化SVM参数,得到了较优的结果。梁坚等人[10]将小波变换引入到支持向量机中,预测的平均绝对百分比误差减小到了4.54%。在支持向量机模型的研究中,参数优化是模型建立的关键,本文提出了采用领导者策略的狼群搜索算法(wolf colony search algorithm based on the strategy of the leader,LWCA)对支持向量机模型中的参数寻优,建立了LWCA-SVM模型,对二河水源地水质进行了预测,得到了较高精度,为水源地水质预测提供了一种新方法。
1 模型理论分析
1.1 支持向量机模型基本原理
支持向量机主要解决非线性问题,基于统计学的VC维理论和结构风险最小化的原则,利用核函数,通过求解二次型寻优问题,将复杂的非线性问题转化为线性问题,获得其最优解。支持向量机在小样本、非线性、高维空间和过学习问题上具有独特的优势,同时推广适应能力突出[6]。
支持向量机水质预测模型的基本思想是:先将输入的向量通过一个非线性的映射将其映射到一个高维的空间中,然后在这个多维空间中进行线性回归,最后得到一个包含了多因素最优的水质回归函数[11]。
设训练样本为(xi,yi),(i=1,2,…,n),其中,xi=[xi1,xi2,…,xiD]为一个D维的输入向量,yi为输出向量。在高维映射中建立回归函数:
f(x)=wφ(x)+b
式中:w,b为参数;φ(x)为非线性映射函数;f(x)为预测值。
定义不敏感损失函数:

式中:f(x)为预测值;y为真实值;ε为不敏感系数。
引入松弛变量,则问题转化为寻找参数w,b:
式中:C为惩罚函数;ξi,ξ*i分别为控制输出约束的松弛变量的上限和下限。
通过引入Largrange函数,转化为对偶形式求解,最终回归函数为:
式中:αi,α*i,w*,b*为参数;K(xi,x)为核函数。
核函数的选择、惩罚函数C和核函数参数的确定是支持向量机模型建立的重点。其中,核函数的选择是核心问题,一般常用的核函数有多项式核函数、径向基核函数、Sigmoid核函数等,由于多项式核函数运算速度较慢,sigmoid核函数常常收敛效果差[1],而径向基函数是局域核函数,将输入样本映射到高维空间中来解决非线性关系中多个独立变量与因变量之间的关系,适合处理水质预测中的复杂的非线性问题,同时径向基函数的参数只有γ,因此本文选取了径向基核函数[10],其表达式为:
K(xi,x)=exp(-γ‖xi-x‖2)
式中:γ为参数;xi和xj是输入样本。
因此, LWCA-SVM数学模型表达式为:
式中:M为LWCA优化SVM的误差;y(xj)为实测值。
1.2 领导者策略的狼群搜索算法
网格搜索法、粒子群算法和遗传算法是支持向量机模型中常用的参数寻优方法。但是网格搜索法[12]需要把整个空间划分网格,参数的寻优依赖于网格的划分,寻优时间长,误差大;粒子群算法[13]往往得到的是局部最优结果;遗传算法[14]需要编码,交叉变异,计算复杂度高。因此本文提出了领导者策略的狼群搜索算法对参数进行寻优,减少了算法的复杂程度,利用优胜劣汰保证了最优解为全局最优。
领导者策略的狼群搜索优化算法是一种群体性的智能优化算法,美国著名研究专家Mesh[15]在1970年出版的专著中详细描述了群狼的生存捕猎行为,在2007年首次提出了狼群算法[16]。狼群算法最终归纳为捕猎和遇到威胁逃跑等行为[17-19]。通过对狼群算法的改进,成功在机器人路径规划[20]、水电站优化调度[21]和无人机航迹规划[22]中等得到了应用。
在捕猎过程中,部分比较强壮的狼相互竞争得到领导者,其他狼在领导者的召唤下,有组织地去包围猎物。在捕猎的过程中,部分比较强壮的狼不断的竞争,使得领导者不断地更新。最后,通过优胜劣汰淘汰掉那些弱小的狼。因此,领导者策略的狼群搜索算法包括了狼群的初始化、竞争领导者、向领导者移动、包围猎物和优胜劣汰五个步骤[19]。
(1)狼群初始化。为了满足初始狼群在定义域内均匀地分布,将n匹狼在D维空间内进行初始化,其中,第i只狼的位置为:
Xi=(xi1,…,xid,…,xiD) 1≤i≤N,1≤d≤D
xid=xmin+rand×(xmax-xmin)
式中:rand是在[0,1]之间的随机数;xmax和xmin分别是第i维空间下的最大值与最小值。
(2)竞争领导者。选取q匹最优的狼在h个方向周围进行搜索,当前位置为:Pi(pi1,…,pid,…,piD)。围绕着当前位置P0产生P1,如果当前产生的P1优于P0,则将替代,否则保留原始位置。最大搜索次数为dhmax。
竞争狼产生的h个点位置中第j个点的d维位置yjd(1≤j≤h)为:
yjd=xxid+rand×stepa
式中:rand是在[0,1]之间的随机数;xxid是j匹狼的第d维的位置;stepa为搜索的步长。竞争狼搜索结束后,寻找出最优的狼作为领导者。
(3)向领导者移动。为了搜寻猎物,其他狼向领导者移动,这些狼在移动过程中,可能会发现其他猎物,则可能远离领导者,第i只狼更新位置zid为:
zid=xid+rand×stepb×(xld-xid)
式中:rand是在[0,1]之间的随机数;xid为第i只狼的d维位置;stepb为移动步长;xld为领导者d维位置。向领导者搜寻结束后,再次寻找最优的狼作为领导者。
(4)包围猎物。领导者搜寻到食物后,通过嚎叫通知其他狼包围猎物。首先在[0,1]内产生随机数rm,如果比θ(预先设定的一个阈值)小,则不移动,否则,进行包围,更新后的位置Xt+1i为:
式中:ra为包围步长;Xl为领导者位置;Xti为迭代t次第i只狼的当前位置。
包围后的狼,可能不在定义域内,因此需要越界处理:
随着迭代次数的增加,越来越接近最优位置,因此包围步长要进行不断的减小,包围步长的变化公式:
式中:t为迭代次数;maxt为最大迭代次数;ramax和ramin为最大最小包围步长。
(5)优胜劣汰。根据优胜劣汰原则,在所有狼中,m匹弱小的狼需要被m匹强壮的狼进行替代,保证狼群生存下去,这种方法也避免了寻优过程中出现局部最优化的弊端,体现了狼群多样性的特点。
2 LWCA-SVM模型构建
基于领导者策略狼群搜索算法的支持向量机水质预测模型,如图1所示。
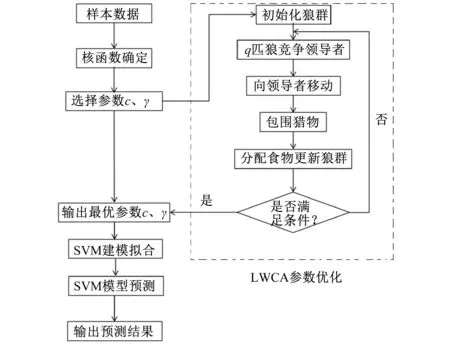
图1 LWCA-SVM模型计算图
首先将水质理化指标与水质参数进行相关性分析,然后进行偏自相关分析,分别得到不同水质参数的滞后时间,确定支持向量机模型的输入与输出,即:x=(x1,x2,…,xn),n为输入样本的组数。输出向量为需要预测的水质f(x)=[f(x1),f(x2),…,f(xn)]。其中,每一个输入xi包含了其他水质参数和自身的几组水质参数。利用基于领导者策略的狼群搜索算法对支持向量机(SVM)中参数C和γ求最优解,对领导者策略狼群搜索算法中的参数进行敏感性分析,寻找出最优的参数。将得到的最优参数代入模型中训练,最终利用率定的模型对水质参数进行预报,并进行误差分析。
本文选择了均方误差(Mean Squared Error,MSE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)和Pearson系数3个指标评价模型的合理性,MSE和MAPE越小,Pearson系数越大,预测效果越好。
式中:f(xi)为预测值;yi为实测值;n为样本个数。
3 仿真与结果分析
3.1 研究区域及其水质状况
二河闸位于二河流域的上游,是洪泽湖出湖的主要控制工程,距洪泽湖出水口1 km左右。自1958年建成以来,二河闸发挥了泄洪、航运、灌溉、供水等重要作用,如洪泽湖可通过二河闸下泄补给二河,其附近的水质指标能在一定程度上反应“二河水功能区”的水质情况[23]。
作为洪泽湖主要出水口之一的二河,水质的好坏主要取决于洪泽湖水质状况。近年来,洪泽湖透明度降低,TN和TP严重超标,导致湖体一直处于富营养化状态,这也是二河水质TN和TP超标的主要原因[24]。二河闸周围的农田区域农药大规模的使用,在降雨过程中雨水冲刷土壤,营养盐等流入水体,加剧了水体的富营养化[25]。
3.2 研究区域与水质参数相关性分析
本文采用的水质数据来源于淮安环保局网站公布的2015年饮用水源地的水质数据,其数据是采用断面检测仪自动监测二河闸断面的水质,文章选取了对水质敏感的水温、pH、DO、TN、TP等进行分析预测,分析确定了水温、pH和DO(TN、TP)作为输入变量,为了保证对水质预测有一个全面的分析,同时避免水质监测过程中的偶然性,将环保部公布连续5天的数据取平均值作为一个样本,从2015年1月1日到12月26日记录了73组数据,对DO、TN和TP进行预测。在Matlab14a运行环境下,运用台湾林志仁教授开发的LIBSVM工具箱[27]编程进行了仿真实验。
通过Pearson相关性求解,得到溶解氧与pH和水温在0.05显著水平下的相关性为-0.724和-0.828,然后对溶解氧、pH和水温分别求偏自相关系数,得到溶解氧、pH和水温的滞后时间都为5 d。具体的模型输入与输出关系见表1。而TN与pH和水温在0.05显著水平下的相关性为0.082 8和0.111 5,TP与pH、水温在0.05显著水平的相关性分别为-0.002 4和0.000 1,相关性很低,因此,TN与TP的模型的输入只利用自身序列数据预报。对TN和TP进行偏自相关性分析,得到TN的滞后时间为25 d,TP的滞后时间为25 d,具体输入与输出关系见表1。

表1 LWCA-SVM模型的输入与输出
表中k表示样本的编号, 样本中第i组预测值,s与k相差个数为温度滞后个数加1个单位,m+与k相差个数为pH滞后个数加1个单位。DO的k、s和m都为1,TN和TP的k都为5。因此前65组样本用作DO训练模型,前61组样本用作TN预测模型的训练,前61组样本用作TP预测模型的训练,剩余的7组作为验证样本。
3.3 参数敏感性分析
文献[17]中对领导者策略的狼群搜索算法中的参数进行了初步的研究,对单峰函数和多峰函数求解都得到了很好的结果,对奔袭步长的敏感性做了分析[19],发现奔袭步长在1.5~2.5之间计算最稳定,效果最好,模型参数是否适用于支持向量机模型还需要进一步的检验。
由于DO的输入输出关系比较复杂,因此在敏感性分析时,选用了DO的输入输出。本文根据文献,将参数的设置如下:迭代步数800,竞争首狼的个数为5,搜索方向为4,最大搜索次数为15,搜索步长为1.5,移动步长为0.9,最差狼为5个,参数θ为0.2。其中,初始化狼群个数是影响模型计算时间长短的重要因素,因此本文对这个参数进行了敏感性分析。在试算过程中,分别将初始化狼群个数设置为20,40,80,100,150,200,250,300。每个试算点进行20次独立求解,最后根据MSE的平均值和标准差两项指标进行综合的选择。
通过对初始狼群的敏感性分析可以得到(表2),当初始狼群的数量大于等于150时,MSE平均值和标准差趋于稳定,说明此时算法寻优比较稳定。
3.4 二河闸水质预测效果
根据初始狼群的敏感性分析,本文选用的初始狼群为150。
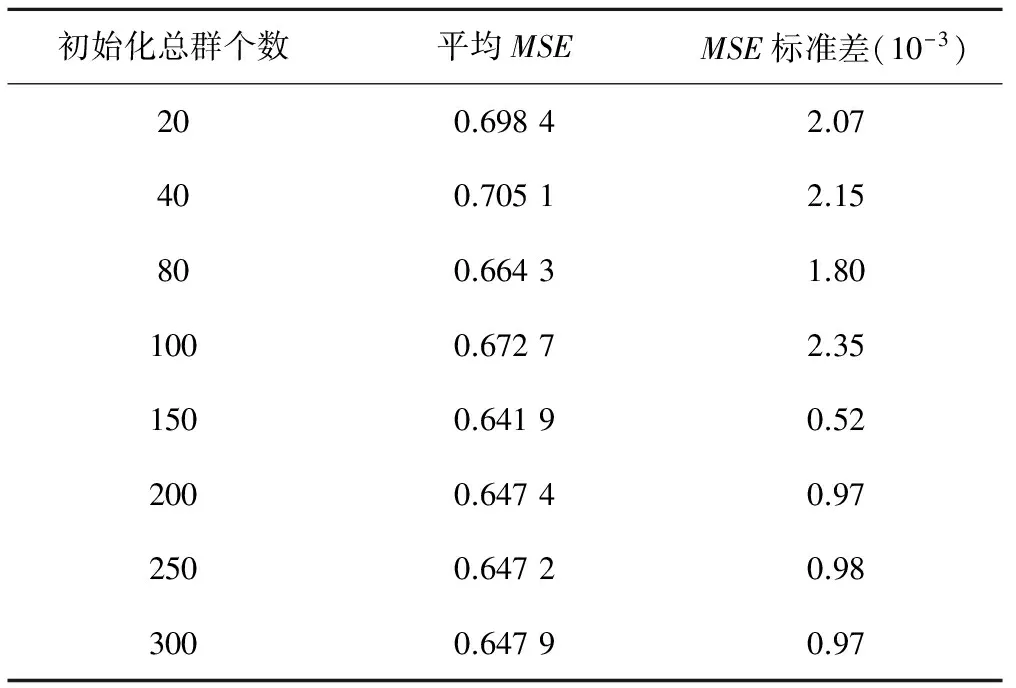
表2 初始化狼群个数敏感性分析结果
对DO、TN和TP利用领导者策略的狼群搜索算法寻优得到了最优参数,领导者策略的狼群搜索算法的寻优过程以TN为例,如图2所示。
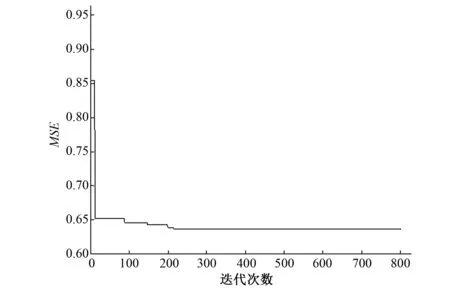
图2 领导者策略的狼群搜索算法参数寻优过程
利用领导者策略狼群搜索算法对支持向量机多目标函数进行参数寻优,得到DO、TN和TP的组合最优参数C和γ如表3所示,将最优参数代入模型中训练,得到3个水质拟合图如图3所示。

表3 不同预测模型的最优参数
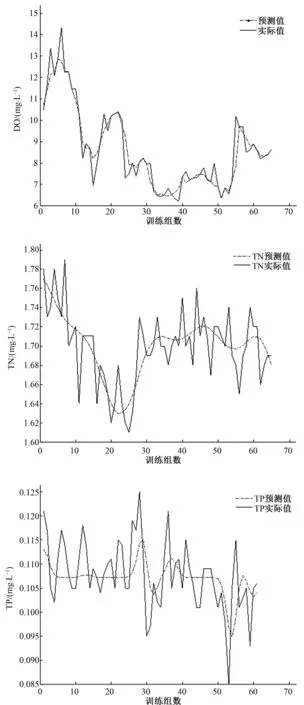
图3 训练实际值与拟合值的比较
样本训练后,可以看出预测曲线逼近实测线,具有较好的拟合性能。DO训练样本的MSE为0.315,MAPE为3.44%;TN训练样本的MSE为2.04×10-4,MAPE为0.82%;TP训练样本的MSE为3.83×10-5,MAPE为4.63%。拟合效果最好的DO的Pearson系数为0.957,TN次之为0.920,TP最小为0.902,表明了LWCA-SVM模型具有很好的学习能力。根据LWCA得到的最优参数,用前一天的参数代入模型中预测后一天的值,最佳参数不变,预测另外7组数据,并分析预测的相对误差、MSE、MAPE和Pearson系数,得到的结果如表4所示。

表4 预测结果分析(DO)
模型进行验证后显示,DO、TN和TP的预测具有较高的精度。由于TN、TP的波动最小,DO的波动最大,因此最终DO的MSE差别较大,但误差都很小;DO的MAPE在3个水质指标中最大,为6.7%,TN最小为0.50%。并且进行Pearson相关性分析,得到DO、TN和TP的实测值的趋势和预测值的趋势高度吻合。它们的相对误差都在14.87%以内,结合MSE、MAPE、和Pearson相关系数,说明模型对富营养化指示因子TN、TP和波动幅度较大的DO具有较高的预测精度,建立LWCA-SVM模型在饮用水源地水质预测中推广适应能力强,能够为二河闸饮用水源地水质预测提供新途径和方法。预测值与实测值之间仍然存在一定的误差,主要是实测值频次少,与实际河湖水体水质存在一定差距,同时污染源的排放和降雨量、径流量等水文条件随时间不断地变化也会导致实测值与预测值之间的误差[6],另外模型中次要参数,如:搜索步长stepa、移动步长stepb、包围步长ra等利用经验值具体确定,因此使得实测值与预测值也存在一定误差。
4 结 语
将LWCA的全局寻优的优势和SVM的结构风险最小化的优点结合,建立了LWCA-SVM模型,通过对初始狼群的敏感性分析,得到当初始狼群数量为150时,算法稳定,寻优能力最佳。同时,采用LWCA-SVM水质预测模型对二河闸水质的TN、TP和DO 进行了预测,预测精度高,说明模型在人为活动影响条件复杂、水体营养物含量多的河湖水域水质中能够准确地预测,并且在短时水质预测中体现出较高的精度,为区域水污染控制系统规划与水源地水质有效管理提供技术支持。
□
[1] 陈为国,许文杰.湖泊生态系统服务功能影响因子分析与评价研究[J].节水灌溉,2010,(12):35-37.
[2] 陈江龙,徐梦月,魏文佳,等.湖泊型水源地管理研究-以苏州市太湖水源地为例[J].长江流域资源与环境,2012,21(7):836-842.
[3] 周晓铁,韩宁宁,孙世群,等.安徽省河流和湖库型饮用水水源地水质评价[J].湖泊科学,2010,22(2):176-180.
[4] 淮安水利局:http:∥slj.huaian.gov.cn/slzx/mtbd/5e38cfb851601858015165dab6fc1759.html.
[5] 袁宏林,龚 令,张琼华,等.基于BP神经网络的皂河水质预测方法[J].安全与环境学报, 2013,13(2):106-110.
[6] 张秀菊,安 焕,赵文荣,等.基于支持向量机的水质预测应用实例[J].中国农村水利水电,2015(1):85-89.
[7] Xu Longqin,Liu Shuangyin.Study of short-term water quality prediction model based on wavelet neural network[J]. Mathematical and Computer Modelling, 2013,58(3-4):807-813.
[8] 刘双印,徐龙琴,李振波,等.基于PCA-MCAFA-LSSVM的养殖水质pH值预测模型[J].农业机械学报,2014,45(5):329-246.
[9] 程庭莉.基于支持向量机的三峡库区水质预测与评价方法研究[D].重庆:重庆大学,2013.
[10] 梁 坚,何通能.基于小波变换和支持向量机的水质预测[J].计算机应用与软件,2011,8(2):83-86.
[11] 杨会娟,粟晓玲,郭 静.基于支持向量机的干旱区月潜在蒸发的模拟[J].中国农村水利水电,2016,(7):6-10.
[12] Kohavi R. A study of cross-validation and bootstrap for accuracy estimation and model selection[C]//IJCAI, 1995,14(2):1 137-1 145.
[13] Kennedy J, Eberhart R. Particle swarm optimization[C]∥Proceedings of IEEE international conference on neural networks. 1995,4(2):1 942-1 948.
[14] 王银年.遗传算法的研究与应用[D].江苏无锡:江南大学,2009.
[15] Mech L D. The Wolf: the ecology and behavior of an endangered species[M]. USA: New York Natural History Press, 1970.
[16] YANG Chenguang, TU Xuyan, CHEN Jie. Algorithm of marriage in honey bees optimization based on the wolf pack search[C]∥ Proceedings of IEEE Computer Society International Conference on Intelligent Pervasive Computing. Jeju Island:[s.n.],2007:462-467.
[17] LIU Changan,YAN Xiaohu,LIN Chunyang,et al. The wolf colony algorithm and its application[J]. Chinese Journal of Electronics,2011,20(2):212-216.
[18] TANG Rui, SIMON Fong, XIN Sheyang, et al. Wolf search algorithm with ephemeral memory[C]∥ Proceedings of IEEE Digital Information Management (ICDIM) Seventh International Conference. Macau:[s.n.],2012:165-172.
[19] 周 强,周永权.一种基于领导者策略的狼群搜索算法[J].计算机应用研究,2013,30(9):2 629- 2 632.
[20] 鄢小虎.基于生物智能的移动机器人路径规划研究[D].河北保定:华北电力大学, 2010.
[21] 王建群,甲洋洋,肖庆元. 狼群算法在水电站水库优化调度中的应用[J].水利水电科技进展,2015,35(3):1-4.
[22] 刘永兰,李为民,吴虎胜,等. 基于狼群算法的无人机航迹规划[J].系统仿真学报,2015,27(8):1 838-1 843.
[23] 薛峰,韩智,蒋明学.二河闸钢闸门更换施工[J].水利规划与设计,2005,(3).
[24] 李 波,濮培民.淮河流域及洪泽湖水质的演变趋势分析[J].长江流域资源与环境,2003,12(1):67-73.
[25] 宓永宁,陈 默,张 茹.灰色拓扑法在大伙房水库总氮预测中的应用[J].水利建设与管理,2009(3):72-73.
[26] 市区饮用水源水质:http://hbj.huaian.gov.cn/web/hbj/4924/6100/6100.shtml.
[27] 王晓云. SVM算法分析与研究[J].渝西学院学报(自然科版),2005,4(3):15-18.
