大坝实测服役性态抗噪预测模型

杨 贝 贝

(1. 河海大学水文水资源与水利工程科学国家重点实验室，南京 210098；2. 河海大学水利水电学院，南京 210098)

利用大坝变形、渗流、应力应变等原型监测资料建立预测模型，以分析和预测大坝服役性态，是大坝安全监控的重要内容[1-3]。但实际中监测数据不可避免地受到噪声污染，利用受污染的数据建立预测模型，必然影响模型的精度，进而影响大坝安全分析的准确度。小波分析可以用于时频分析、多分辨率分析，信号和噪声在多尺度空间上具有不同的Lipchitz指数，利用小波分析能有效地去除监测数据中的噪声，为预测模型提供反映大坝实际性态的真实数据[4-6]。目前常用的非线性时间序列预测模型有统计回归模型、ARMA模型、支持向量机回归模型(SVM，Support Vector Machine)以及神经网络模型等[7-9]，其中基于统计学习理论的结构风险最小化以及VC维原理的支持向量机模型，具有泛化能力强、预测精度高等优点，在解决小样本、非线性、高维数问题方面，较其他模型有明显优势，但其精度受惩罚因子以及核函数参数影响较大[10,11]。粒子群算法(PSO，Particle Swarm Optimization)具有算法简单易实现、收敛速度快、可调参数少等优点，利用PSO对支持向量机的参数进行寻优，对提高支持向量机模型预测精度是一个很好的尝试[12]。

文中基于上述背景和目标，综合应用小波、支持向量机(SVM)、粒子群算法(PSO)等数学和智能算法工具，开展了大坝实测服役性态抗噪预测模型的构建方法研究，并将其应用于某实际大坝工程问题的分析，通过与传统统计回归模型的对比，验证了所述方法和模型的可行性和工程实用性。

1 基于PSO-SVR的大坝实测服役性态抗噪预测模型建模原理

1.1 大坝原型监测数据小波分析与去噪

小波分析具有时频分析、多分辨率分析等优点，大坝原型监测设施所获取的监测数据，包含了实际信号和(误差)噪声信号2部分。设f(t)是原型监测设施观测到的数据，则有：

f(t)=s(t)+n(t)

(1)

式中：s(t)是原始信号，即实际原型监测数据；n(t)为噪声信号。

去噪的目的就是从含噪信号中得到在某种误差估计下信号f(t)的最优逼近信号f(t)。

信号经小波变换后，产生的小波系数包含有信号的重要信息，其幅值大数目小，而噪声对应的小波系数幅值小。阈值滤波有软阈值滤波和硬阈值滤波。硬函数有间断点，只是简单的保留或者去掉信号，本文采用软阈值滤波[13]。

软阈值函数：

(2)

式中：T为所选阈值。

通过在不同高频序列尺度上选取合适的阈值，将小于该阈值的小波系数置零，保留大于该阈值的小波系数，最后进行小波逆变换，得到滤波后的重构信号。

1.2 大坝实测服役性态预测的抗噪SVM模型

非线性支持向量机回归(SVM)的基本思想是通过一个非线性映射φ将数据x映射到高维Hilbert空间，然后在这个高维空间进行线性回归计算，这样低维输入空间的非线性回归就转换为高维特征空间的线性回归。核函数k(xi,xj)=φ(xi)×φ(xj)是实现这种转换的关键。

用函数f(x)=wφ(x)+b估计去噪后的数据{xi,yi}，i=1,2,…,l，xi∈Rn，yi∈R，引入松弛变量ξi，ξ*i。假定存在函数f在ε精度下能够估计所有的(xi,yi)数据，那么寻找最小w的问题可以表示成凸优化问题：

(4)

引入拉格朗日函数和对偶变量：

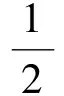
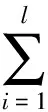
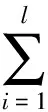
(5)

式中：ηi，η*i，αi，α*i大于或等于零；C>0。

根据KKT条件：

(6)

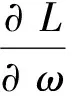
(7)

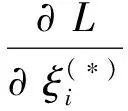
(8)

(9)

最大化式(9)求得参数αi，α*i，最后可得回归函数：

(10)

本文采用RBF核函数，公式如下：

(11)

式中：x为核函数中心；σ为函数的宽度参数。

1.3 基于PSO的大坝实测服役性态预测模型优化

粒子群优化算法是一种基于群体智能优化算法。粒子群中优化问题的每一个可能解称为粒子，每个粒子的优越程度由定义的适应度函数决定。在n维搜索空间中，每个粒子表示为该空间中的一个点，用xi=[xi1,xi2,…,xin]表示，第i个粒子最优解表示为pbesti=[pi1,pi2,…,pin]，种群的全局最优解表示为gbest=[g1,g2,…,gn]，经过k次迭代后粒子移动速度表示为vki=[vki1,vki2,…,vkin]，其更新公式为：

vkid=wivk-1id+c1rand1(pk-1id-xk-1id)+c2rand2(gk-1d-xk-1id)

(12)

xkid=xk-1id+vkid

(13)

式中：i=1,2,…,m；d=1,2,…,n；m为粒子群中粒子的个数；n为解向量的维数；k为当前迭代次数；c1和c2分别为非负常数；rand1和rand2为2个分布在[0,1]之间的随机数；wi为惯性权重，其大小代表搜索能力的强弱。

基于PSO-SVM的大坝实测服役性态抗噪预测模型建模流程如图1所示，其中n表示小波分解的层数，i=1,2,…,n。

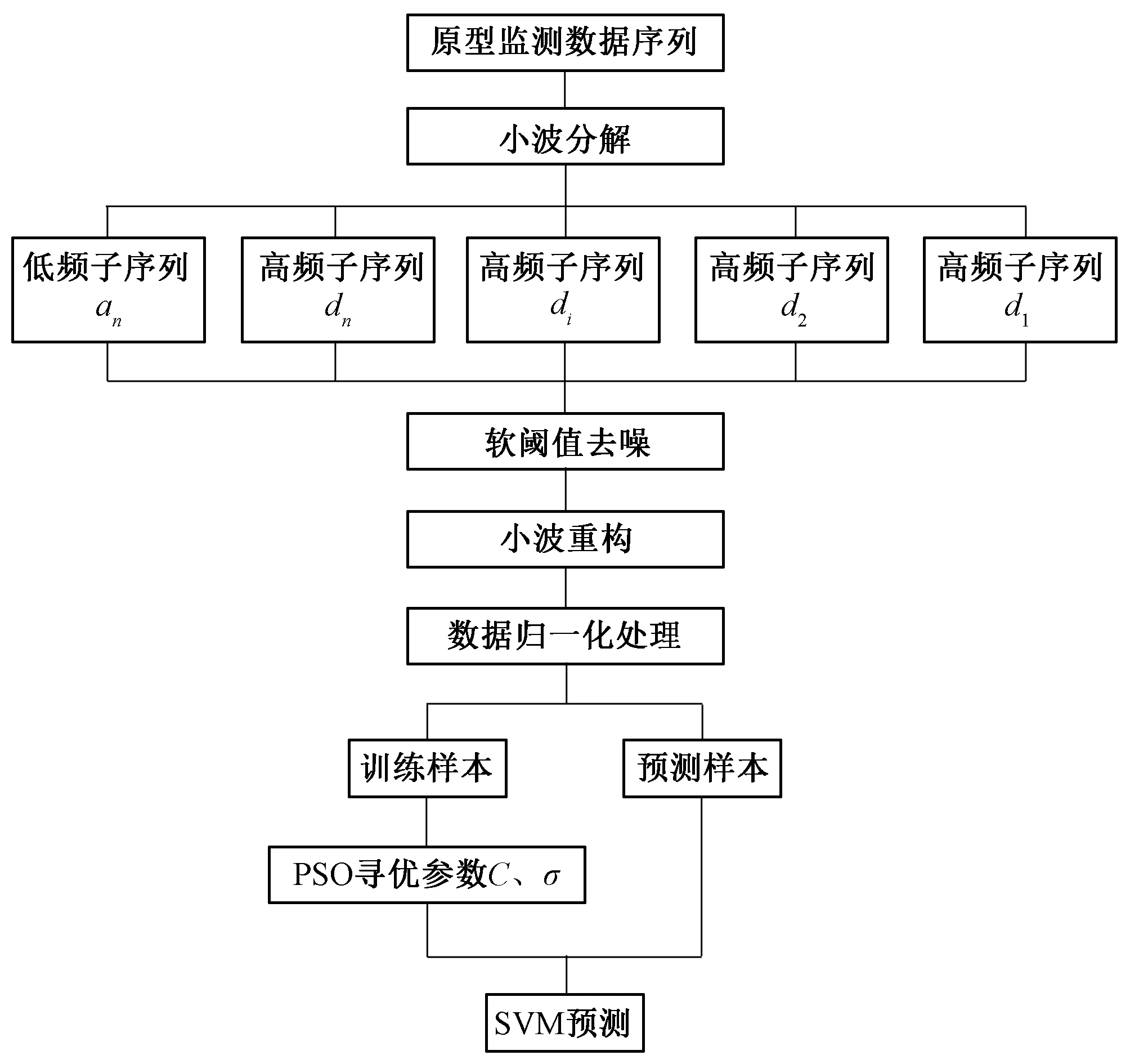
图1 大坝实测服役性态抗噪预测模型建模流程Fig.1 The model of the measured data of the dam for the anti-noise prediction model

2 实例分析

某水库工程位于淠河东源，坝址以上控制流域面积1 840 km2，水库总库容4.91 亿m3，为年调节水库。大坝为钢筋混凝土连拱坝，最大坝高75.9 m(含1982年加高的1.5 m)，坝顶全长510 m，由21个拱、20个坝垛及两端重力坝段组成。水库坝址处水位、流量及降雨量观测始于1951年，多年平均入库流量50.4 m3/s，多年平均来水量15.9 亿m3。选取19号垛的正垂线测点PL19的上下游自动化观测数据为例进行分析。该测点始测于2015年5月1号，选取2010年1月1日-2011年1月25日共380组数据用于拟合，2011年1月26日-2011年2月4日共20组数据用于预测。

2.1 大坝位移监测数据小波去噪

为使去噪后序列足够光滑，采用阶数较高的db4小波对原始数据序列分解为4层[14]，得到低频和高频子序列，如图2所示。

图2 原始监测数据小波分解Fig.2 Wavelet decomposition of the original monitoring data

噪声的存在使高频序列波动较剧烈，选用合适的阈值分别对各高频子序列进行软阈值去噪，将低频序列与去噪后的高频序列用db4小波进行重构，得到去噪后的监测数据序列。去噪后的测值与原始测值对比图如图3所示。可看出阈值去噪的效果还是比较明显的，且原始信号与去噪后信号的残差很小，基本在10-2量级上。

图3 小波去噪效果对比Fig.3 Comparison of the effect of wavelet de-noising

2.2 大坝实测位移性态的PSO-SVM寻优预测

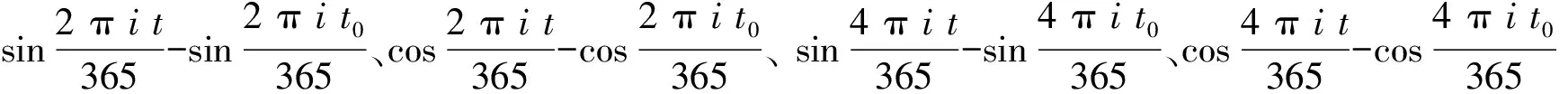
对去噪后的样本数据以及输入变量数据进行归一化处理，使数据在[0，1]之间。初始化种群：粒子个数选为30，种群迭代次数选为100，ε为0.01，c1和c2均定为2，惯性权重 的范围为[1, 0.4]，惩罚因子C的范围为[0.1,100]，核函数σ的范围为[0.01,1 000]。

通过PSO-SVM模型寻优，得惩罚因子C为3.775 1，核函数σ为6.819 2。用PSO-SVM模型和逐步回归模型对训练样本进行拟合，如图4所示，可知PSO-SVM模型的对监测数据的拟合精度明显高于逐步回归模型。

图4 模型拟合曲线对比Fig.4 Comparison of model fitting curves

用PSO-SVM和逐步回归模型对预测样本进行预测，如图5所示，可知PSO-SVM模型对监测数据的预测精度也高于逐步回归模型。

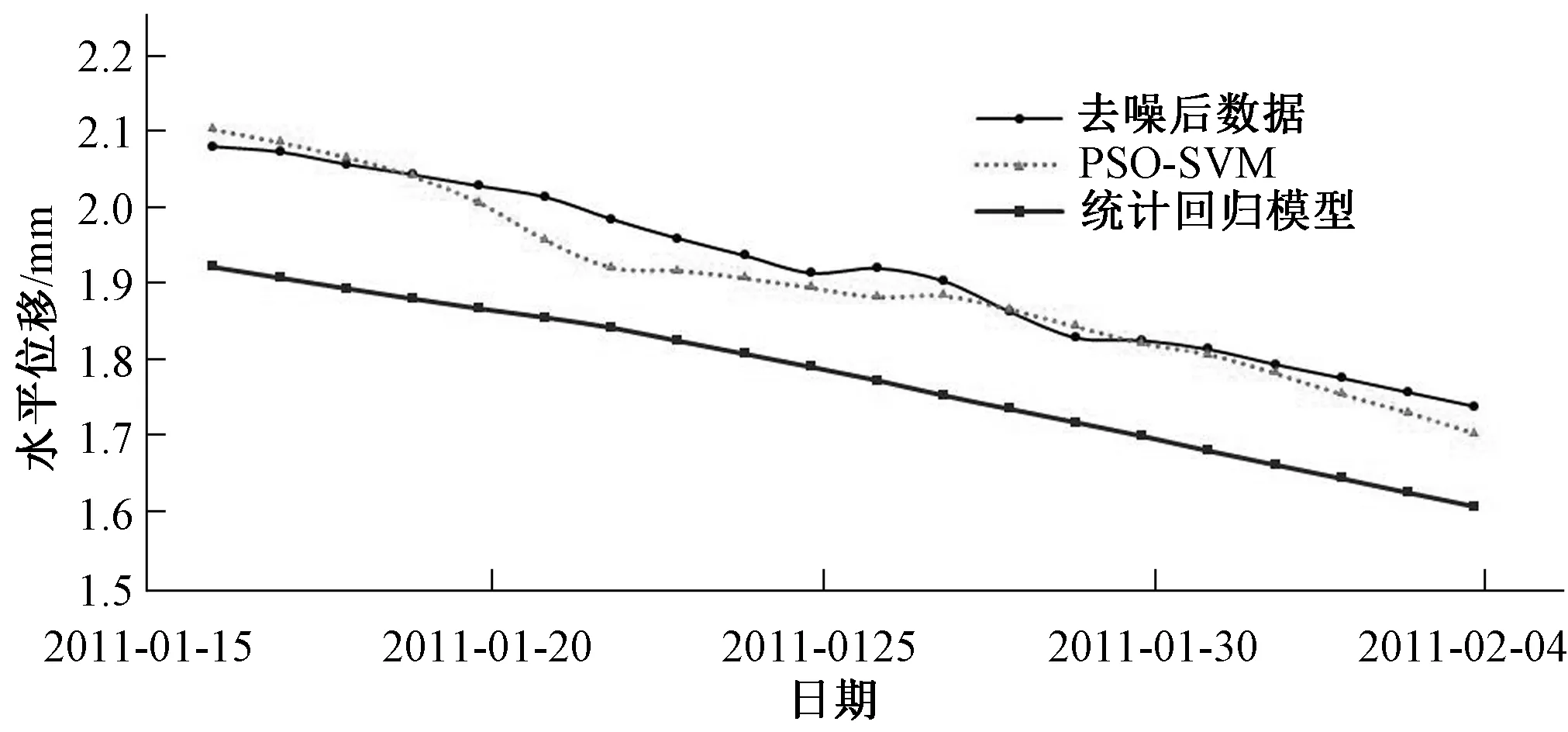
图5 模型预测曲线对比Fig.5 Comparison of model prediction curves

分别计算PSO-SVM模型与逐步回归模型的拟合与预测均方差(MSE)，如表1所示。可知，PSO-SVM模型与逐步回归模型相比，具有泛化能力强、拟合精度高等优点。

3 结 语

大坝变形、渗流、应力应变等服役性态的原型监测数据序列，多具有非线性特征且易受噪声污染。本文以大坝变形监测资料为例，利用小波软阈值去噪法对原始变形监测数据进行去噪处理，得到反映大坝真实变形性态的数据。PSO具有快速全局优化的特点，SVM基于统计学习理论的结构风险最小化原理，能有效地解决小样本、非线性、高维数问题，但其精度受参数的影响较大。为优化预测模型以提高精度，本文建立基于小波去噪的PSO-SVM大坝服役性态预测模型，并将拟合预测结果与统计回归模型作对比，结果表明该模型的拟合精度更高、相关性更好，因此在大坝非线性服役性态预测建模分析中具有实用有效性。

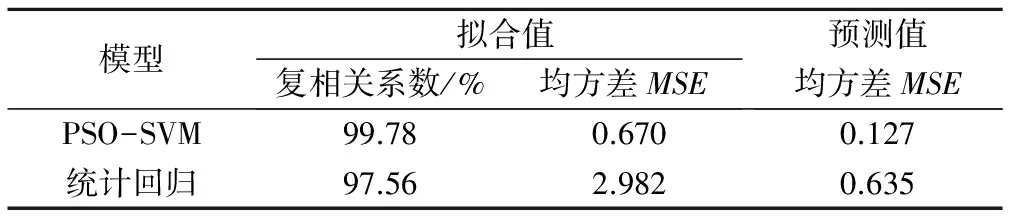
表1 模型均方差Tab.1 MSE of model

□

[1] 吴中如. 水工建筑物安全监控理论及其应用[M]. 北京: 高等教育出版社, 2003.

[2] SU Huaizhi, HU Jiang, WU Zhongru. A study of safety evaluation and early-warning method for dam global behavior[J]. Structural Health Monitoring, 2012,11(3):269-279.

[3] Huaizhi Su, Zhiping Wen, Xiaoran Sun, et al. Time-varying identification model for dam behavior considering structural reinforcement[J]. Structural Safety, 2015,57:1-7.

[4] 潘 泉. 小波滤波方法及应用[M]. 北京:清华大学出版社, 2005.

[5] Huaizhi Su, Zhongru Wu, Zhiping Wen. Identification model for dam behavior based on wavelet network[J]. Computer-Aided Civil and Infrastructure Engineering, 2007,22(6):438-448.

[6] Huaizhi Su, Zhiping Wen, Zhongru Wu. Study on an intelligent inference engine in early-warning system of dam health[J]. Water Resources Management, 2011,25(6):1 545-1 563.

[7] 顾冲时, 吴中如. 大坝与坝基安全监控理论和方法及其应用[M]. 南京: 河海大学出版社, 2006.

[8] Huaizhi Su, Zhiping Wen, Feng Wang, et al. Multifractal scaling behavior analysis for existing dams[J]. Expert Systems with Applications, 2013,40(12):4 922-4 933.

[9] 苏怀智, 王 锋, 刘红萍. 基于POT模型建立大坝服役性态预警指标[J]. 水利学报, 2012,43(8):974-978.

[10] 王定成. 支持向量机建模预测与控制[M].北京:气象出版社, 2009.

[11] 苏怀智, 温志萍, 吴中如. 基于SVM理论的大坝安全预警模型研究[J]. 应用基础与工程科学学报, 2009,17(1):40-48.

[12] 姜谙男, 梁 冰. 基于PSO-SVM的大坝渗流监测时间序列非线性预报模型[J]. 水利学报, 2006,(3):331-335.

[13] 张德丰. MATLAB小波分析[M]. 北京: 机械工业出版社, 2009.

[14] 许哲明. 小波分析在大坝变形监测中的应用研究[D]. 南昌：南昌大学, 2008.