泰森多边形降雨插值方法在流溪河模型洪水预报中的应用

覃建明，陈洋波，王幻宇

(中山大学地理科学与规划学院，广州 510275)

0 前 言

流溪河模型[1,2]是一个精细化的流域洪水预报分布式物理水文模型，其产汇流计算是基于单元网格的，在应用流溪河模型开展流域洪水预报时，需要根据雨量站实测的点降雨，估算各单元上的面雨量。空间插值方法是面雨量估算的主要方法，目前采用的方法主要有泰森多边形法[3,4]、反距离权重法[5]、克里格法[6]、PRISM法[7]、样条插值法[8]等，不同的方法有不同的使用条件。

泰森多边形法[9]是由美国气候学家A. H. THIESS首先提出的一种根据气象站的降雨量推求流域面平均雨量的方法。该方法原理简单而且易于操作，在气象要素空间插值中得到了广泛应用。G.Q Tabios等在美国北部地区应用了不同降雨插值方法并对结果进行分析，发现泰森多边形法和反距离权重法的插值精度相近[10]；徐晶等研究了不同插值方法的优缺点，最后选定泰森多边形法作为全国七大流域计算面雨量的方法[11]；毕宝贵等在海河流域支流选定了较好地反映实际情况的泰森多边形法作为面雨量计算方法，对各支流的实况和预报面雨量进行计算[12]；朱求安等在江口流域采用四种插值方法处理降雨数据并输入新安江模型，发现泰森多边形法取得较好模拟精度[13]；王国庆等在两个不同气候区流域应用水量平衡模型，分析雨量站网密度对月径流模拟的影响，结果表明雨量站网密度对面平均雨量的计算有一定影响[14]；阳帆等应用四种降雨插值方法在三个小流域进行洪水模拟，发现引入泰森多边形的距离反比加权法在模型验证时取得较好精度[15]。

本文的研究目的是探索采用泰森多边形法，为流溪河模型中小河流洪水预报估算单元网格面雨量的可行性。基于泰森多边形原理，本文首先提出了基于泰森多边形法估算流溪河模型单元网格面雨量的方法，针对广东省中小河流田头水流域，建立了流溪河模型，优选了模型参数，模拟了六场实测洪水过程，取得了较好的模拟效果，说明泰森多边形法可以满足流溪河模型洪水预报降雨估算的需要。分析了雨量站网密度对流溪河模型洪水模拟效果的影响，发现存在临界雨量站网密度，当雨量站网密度达到临界值后，利用流溪河模型模拟洪水的变化不大。

1 基于泰森多边形的流溪河模型网格面雨量估算方法

1.1 泰森多边形原理

泰森多边形法又称垂直平分法或加权平均法[16]。该算法的实质是多边形区域的降水强度由其包含的一个唯一气象站降水强度来表示，即将所有相邻气象站用直线连接成若干个三角形，并对三角形作垂直平分线，连接这些垂线的交点组成若干个多边形。将每个多边形内所包含唯一的气象站降雨强度代表这个多边形区域的降雨强度，各个气象站点降雨强度与其所在多边形面积权重的乘积之和为流域平均雨量。计算公式为

式中：fi为第i个雨量站所在多边形的面积，km2；F为流域面积，km2；其余符号意义相同。

该方法原理比较简单而且容易操作，应用比较广泛，适用于气象站空间分布不均匀的地区。当流域内雨量站的数量与位置确定后，泰森多边形的面积权重保持不变，计算工作量较小。

1.2基于泰森多边形的流溪河模型网格面雨量估算方法

流溪河模型[1,2]是一个主要用于流域洪水预报的分布式物理水文模型，采用高分辨率的DEM对整个流域进行划分，从水平方向将流域划分成一系列的单元，单元的尺度一般较小，是一个精细化的分布式物理水文模型。在单元流域上进行蒸散发量及产流量的计算，各单元上产生的径流量通过汇流网络从本单元开始，进行逐单元的汇流，直至流域出口单元。由于流溪河模型的产汇流计算是基于单元层次的，需要根据雨量站的点降雨，估算单元网格上的面雨量。

利用泰森多边形法估算流溪河模型的网格面雨量的方法是，首先根据雨量站的位置，绘制泰森多边形，再根据流溪河模型各网格单元中心的坐标，确定该网格属于哪个泰森多边形内，以位于该多边形内的雨量站的降雨作为该网格的面雨量。

2 研究案例与流溪河模型构建

2.1 田头水流域简介

田头水流域[17]位于广东省北部、湖南省南部，地处广东与湖南交界处，是北江流域二级支流，流域面积523 km2。田头水流域属于山区性河流，洪水陡涨陡落，洪水发生频繁，是广东省洪水灾害防治的重点流域。图1为田头水流域简图。

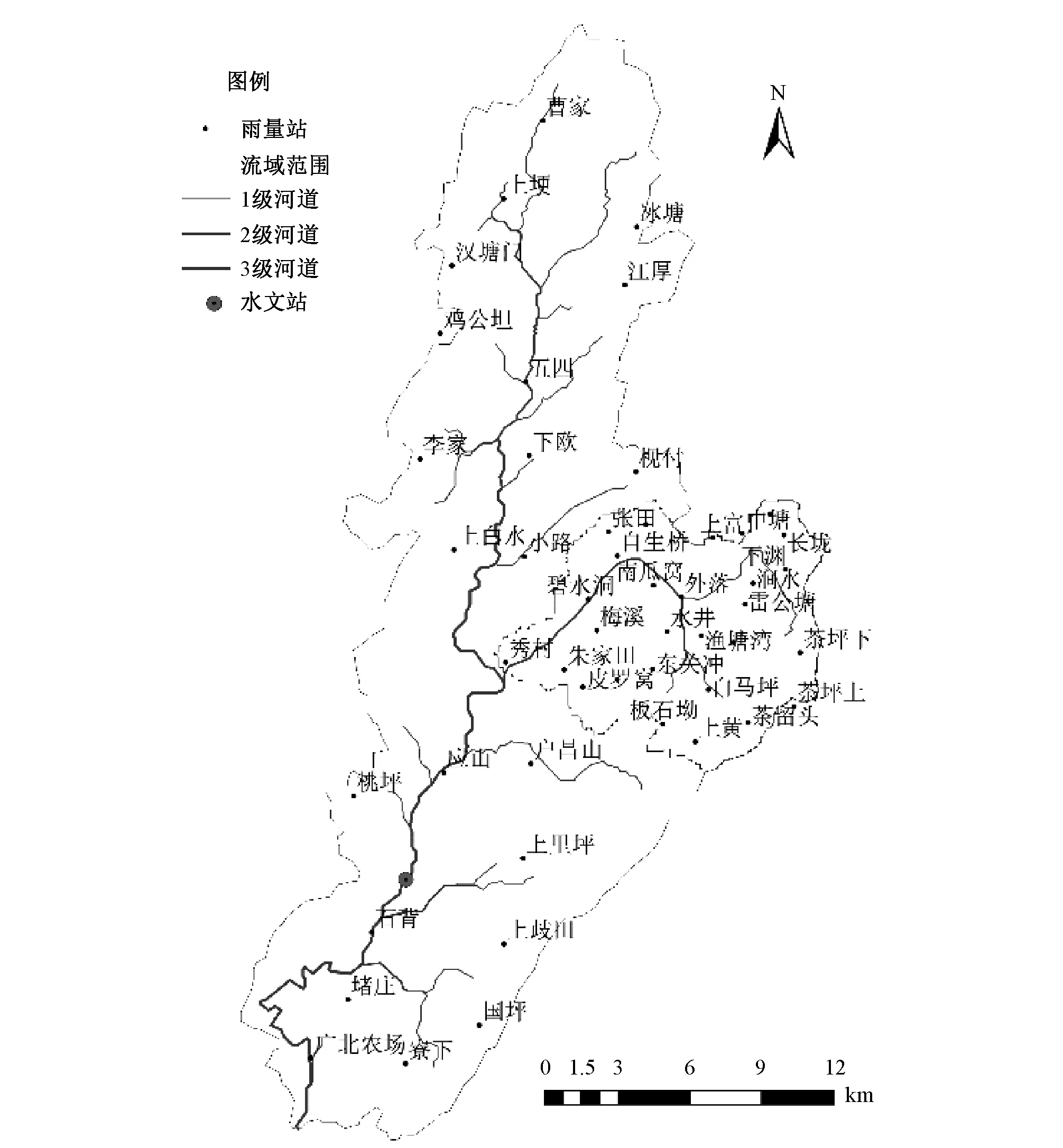
图1 田头水流域简图Fig.1 The map of Tiantoushui Watershed

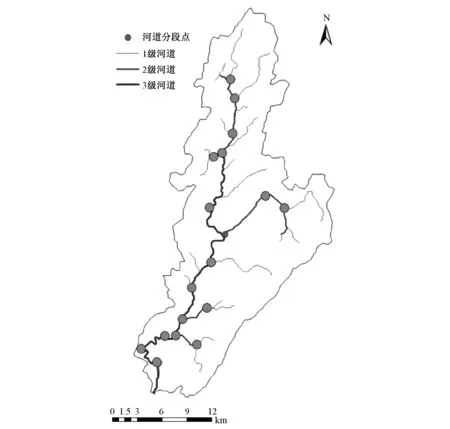
图2 流溪河模型结构示意图Fig.2 Structure of Liuxihe Model in Tiantoushui Watershed

田头水流域内现有50个自动雨量站，其中，一级支流白沙水有30个自动雨量站。田头水流域下游设有赤溪水文站，控制流域面积442 km2。东沙水流域面积90 km2，是典型的山洪灾害易发区。本文研究中，整理出田头水流域2012年至2015年来观测到的七场典型洪水过程资料，包括50个雨量站的降雨及赤溪水文站的流量，作为本文的研究数据。

2.2 流溪河模型构建

按照流溪河模型构建方法，采用空间分辨率为90 m×90 m的SRTM数据库中的DEM对流域进行划分，将单元分成了河道单元和边坡单元。由于流域内没有调蓄能力强的水库，故未划分水库单元。河道划分为3级河网，参照Google Earth遥感影像，设置了河道结点，将河道分成了虚拟河段，并估算了各个虚拟河道的断面宽度、侧坡及底坡。单元分类及河道虚拟结点和虚拟河段的划分结果如图2，其他结果因篇幅限制未列出。

从美国马里兰大学全球观测实验室与中国科学院地理科学与资源研究所联合实验室网站的全球土地覆盖类型数据库中(http:∥landcover.usgs.gov)下载了田头水流域的土地利用类型数据，空间分辨率为1 000 m×1 000 m，通过尺度转换将其转换成与DEM一致的空间分辨率。根据田头水流域的土地利用类型数据，按照流溪河模型中土地利用类型参数的确定方法，确定了边坡糙率和蒸发系数的初始参数值。

从世界土壤信息(ISRIC)网站的全球土壤类型数据库中(http:∥www.isric.org/)下载了田头水流域的土壤类型数据，空间分辨率为1 000 m×1 000 m，通过尺度转换将其转换成与DEM一致的空间分辨率。根据田头水流域的土壤类型数据，按照流溪河模型中土壤类型参数的确定方法，确定了土壤类参数的初始值。

2.3 降雨插值计算

根据泰森多边形插值计算方法，对本文收集的7场洪水过程中的降雨进行了插值计算，得到了各单元上的相应面雨量。图3为部分插值计算结果。

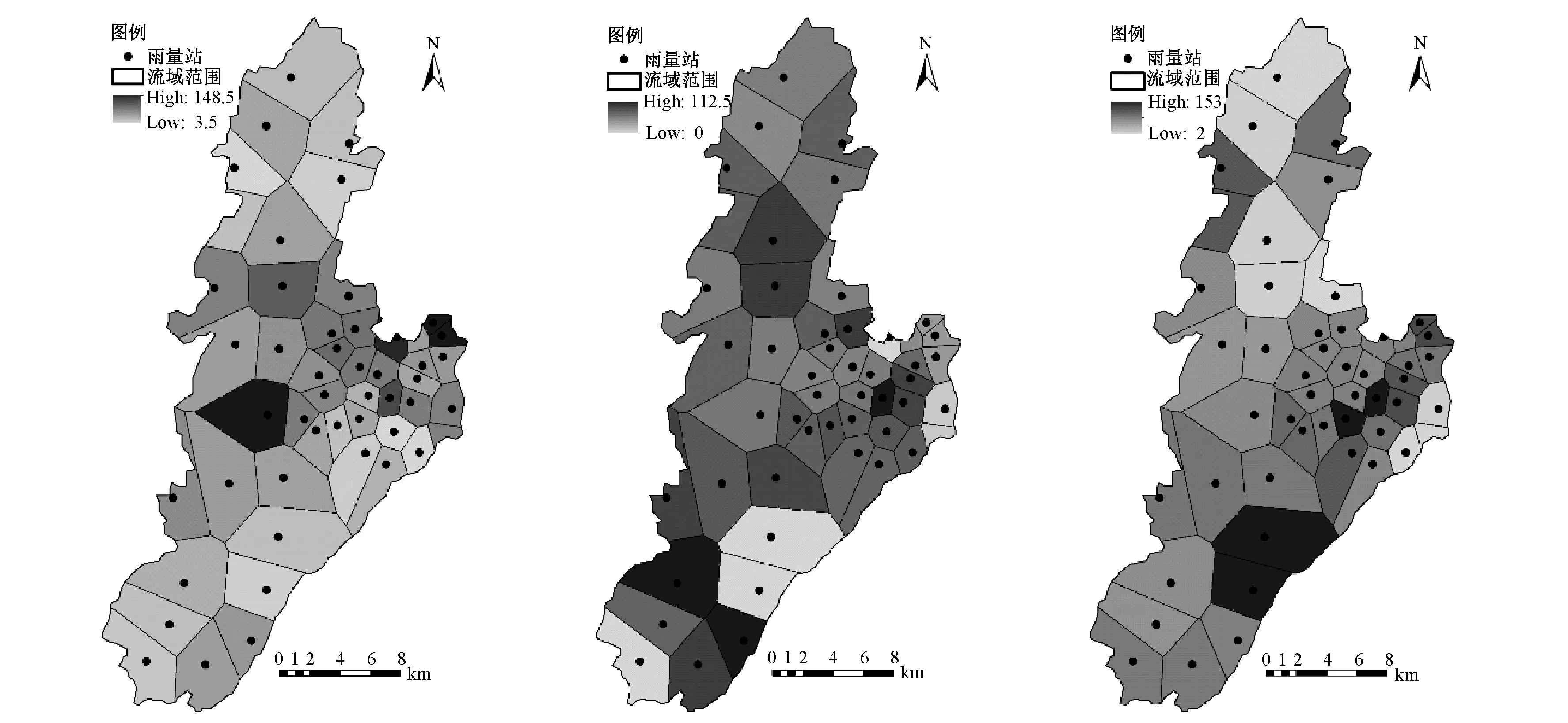
图3 田头水流域部分降雨插值计算结果Fig.3 Part interpolation results of Tiantoushui Watershed

2.4 参数自动优选

采用PSO法[18]对田头水流域流溪河模型12个可调参数进行自动优选。选择20120412场次洪水进行参数自动优选，图4为参数优选计算过程中的部分结果。

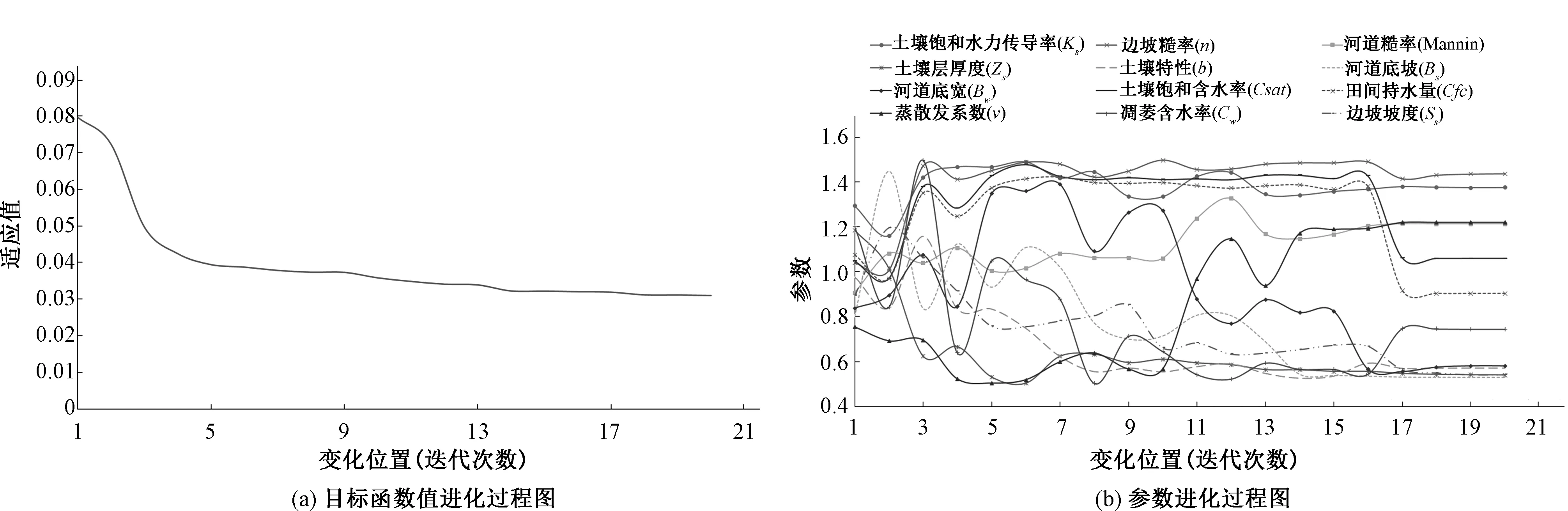
图4 参数优选过程图Fig.4 The evolution process of parameter

本文采用权重法，将五个常用目标函数(确定性系数、相关性系数、过程相对误差、水量平衡系数、洪峰误差)转化为单一目标函数进行参数优选。图4(a)为参数优选过程中目标函数值(适应值)的变化过程，图4(b)为参数的进化过程。从图中可以看出，随着寻优进程的推进，当迭代计算总次数达到18次以后，模型参数值和目标函数值趋近于稳定。

统计该场洪水模拟效果的评价指标，确定性系数为0.919，相关系数为0.973，水量平衡系数为0.854，过程相对误差为30.9%，洪峰相对误差为2.7%，峰现时间差为-1 h，洪水模拟的效果优良。

2.5 模型验证

对2012年到2015年其他的6场洪水进行粒子群算法的适用性验证，并统计了6个评价指标，包括确定性系数、相关系数，水量平衡系数、相对过程误差、洪峰误差，峰现时间差，详细结果见表1。

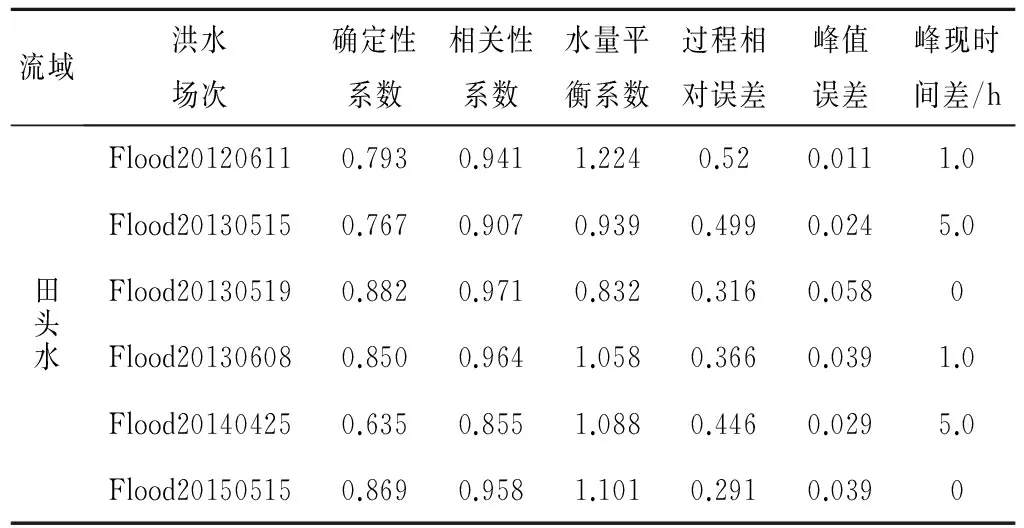
表1 模型验证结果Tab.1 Simulation results of the model

6场洪水模拟过程线分别如图5。

统计模拟效果评价指标，6场洪水模拟的平均确定性系数分别为0.80，平均相关系数分别为0.93，平均水量平衡系数分别为1.04，平均过程相对误差分别为41%，平均洪峰相对误差分别为3.0%，平均峰现时间差均为2 h，洪水模拟的效果优良。表明采用泰森多边形法进行流溪河模型单元面雨量插值计算是可行的。

3 结果与讨论

3.1 雨量站网密度对插值计算结果的影响

田头水流域雨量站网密度较高，插值计算结果较理想，但在很多流域，雨量站网密度相对较低。为了探讨雨量站网密度对降雨插值计算的影响及对流溪河模型模拟结果的影响，对田头水流域50个雨量站，分别抽取其中的5、10、20、30、40、50个雨量站，组成6组不同密度的雨量站网。在选取雨量站时，使雨量站在流域内的分布在空间上尽量均匀。各组的雨量站分布和泰森多边形如图6。

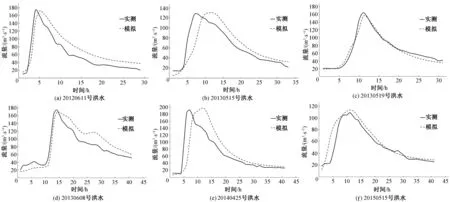
图5 洪水模拟过程图Fig.5 Hydrological process of floods

对6场洪水分别进行插值计算，得到不同雨量站网密度不同场次洪水的流域累积面雨量，结果如图7所示。

从图7结果可以看出，雨量站个数为10个及以上时，流域累积面雨量趋于稳定，变化不大，但当只有5个雨量站时，流域累积面雨量明显不同，说明在本文的研究案例中，当雨量站达到10个时，已基本上能充分反映降雨在流域内的空间变化。这一结果说明，雨量站网密度对估算的流域面雨量有明显影响，当雨量站网密度达到一定值时，雨量站网密度的增加对计算结果的影响不大。

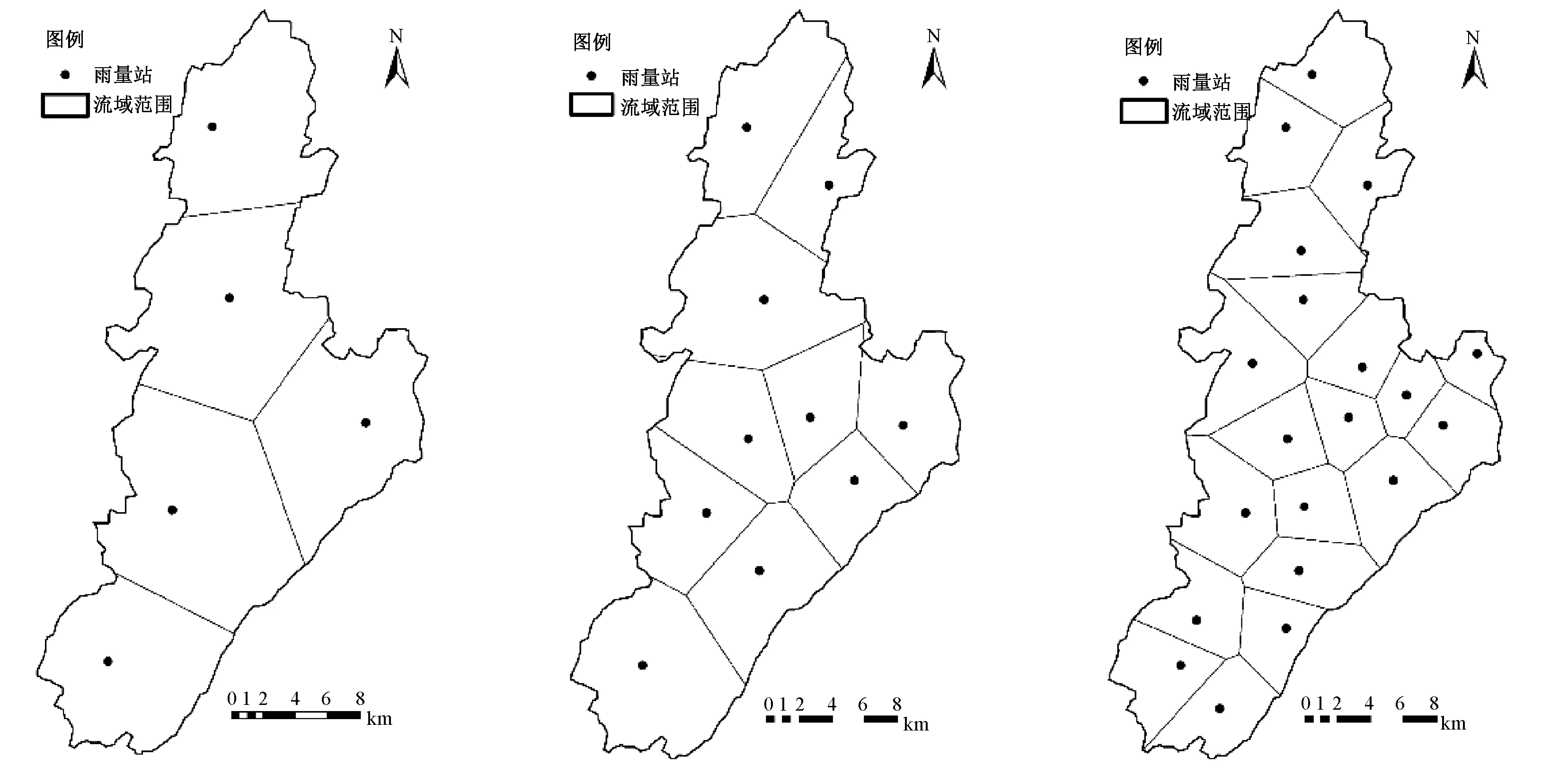
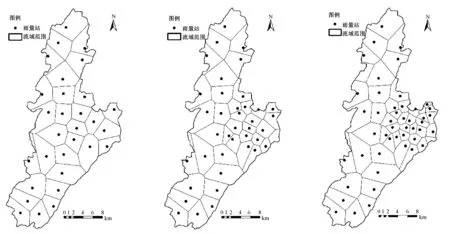
图6 田头水流域雨量站点分布和泰森多边形划分Fig.6 Distribution of gauges and Thiessen polygon of Tiantoushui Watershed

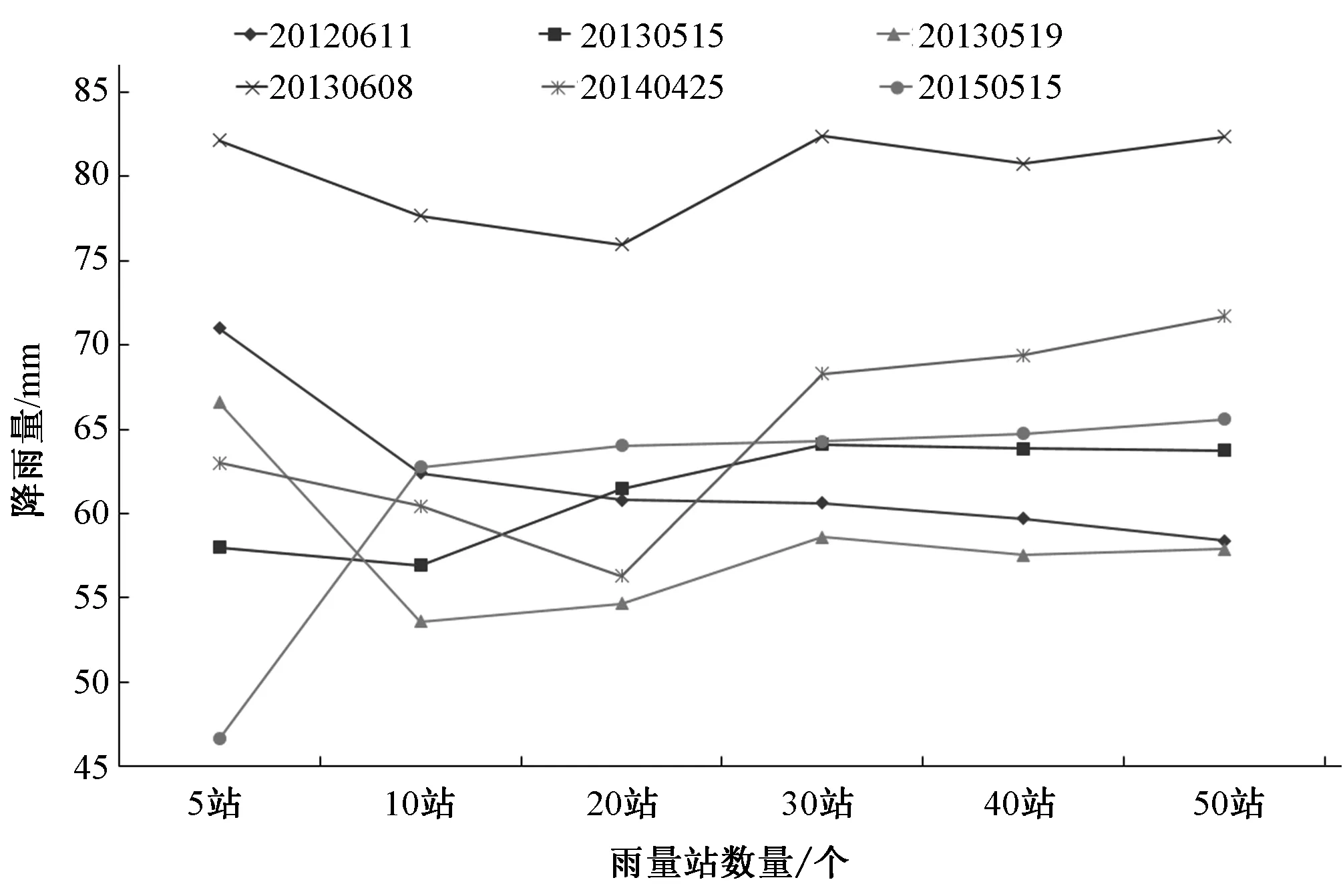
图7 不同站点密度泰森多边形法流域面雨量计算结果对比图Fig.7 The result of rainfall of floods used Thiessen polygon method at different gauge density

3.2 站网密度对流溪河模型参数优选结果的影响

为了分析站网密度对流溪河模型参数优选的影响，利用20120412场次洪水不同站网密度时的降雨插值计算结果，分别进行参数自动优选，结果如图8。

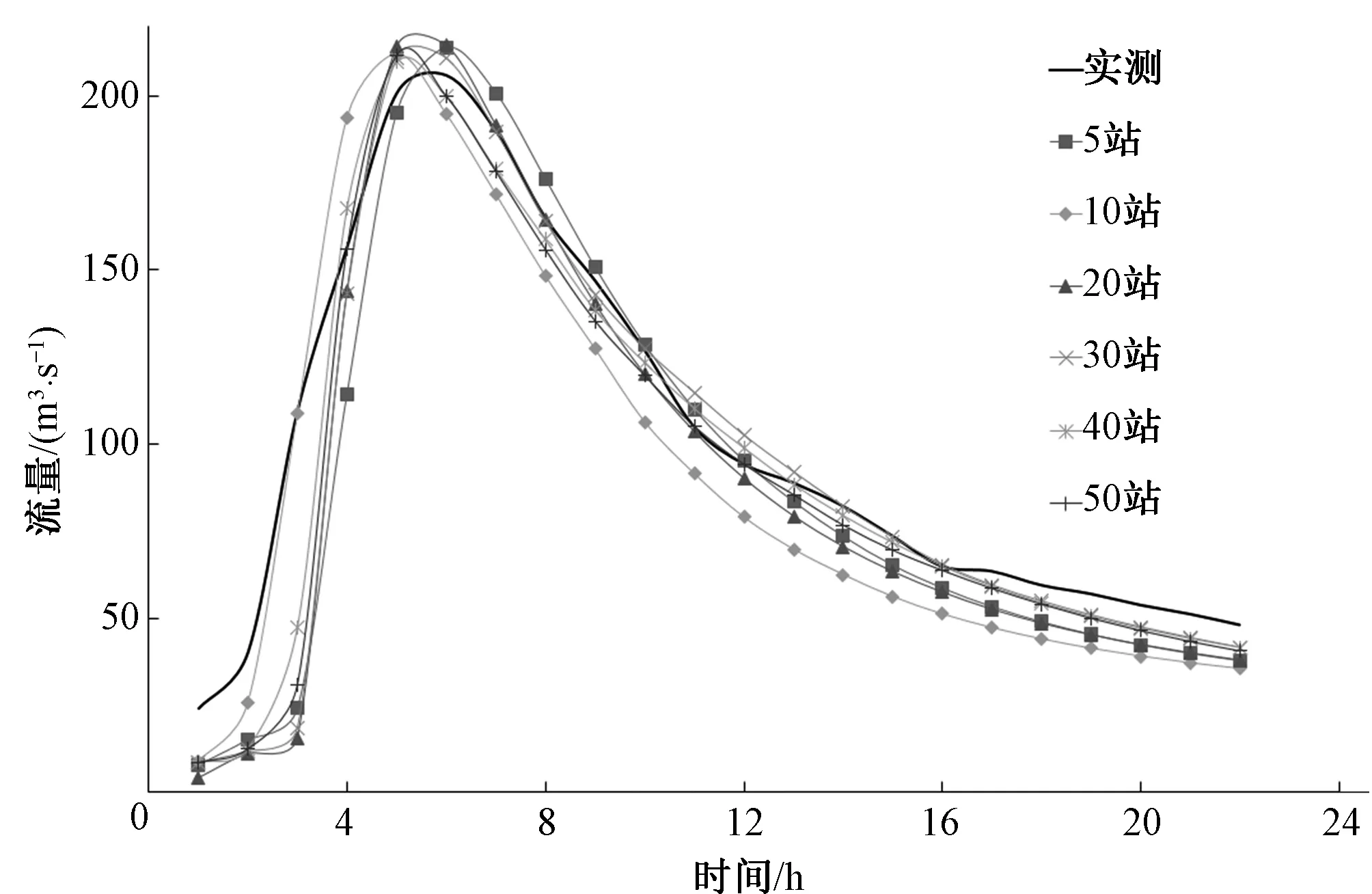
图8 20120412场次洪水不同站点密度下参数优选结果对比图Fig.8 Hydrological process comparison simulated with different gauge density

从上述结果看出，站网密度对流溪河模型参数优选结果的影响较小，这说明流溪河模型在进行参数优选时，可在一定程度上消除降雨空间分布的不确定性。

3.3 站网密度对流溪河模型模拟结果的影响

采用20120412场次洪水不同站点密度下优选的模型参数，对六场次洪水不同站网密度的降雨进行了洪水模拟，结果如图9。

对于前5场次洪水，雨量站点数量从5个变化到50个时，流溪河模型的洪水模拟结果变化较小，可能的原因是本场次洪水的降雨在空间上的变化不大。对于20150515场次洪水，当雨量站个数达到10个后，洪水过程的变化也较小，但当雨量站个数为5个时，模拟的洪水过程与实测值有明显偏差，这说明5个雨量站不能充分测报降雨的空间分布。这也说明在田头水流域，当雨量站个数达到10个时，基本上能测报出降雨在空间分布上的不均匀性。

4 结 语

本文提出了基于泰森多边形法估算流溪河模型单元网格面雨量的方法，针对田头水流域建立了流溪河模型，采用PSO算法优选了模型参数，模拟了六场实测洪水过程，取得了较好的模拟效果，说明泰森多边形法适用于流溪河模型洪水预报降雨估算的需要。 分析了站网密度对面雨量估算、流溪河模型参数优选及洪水模拟的影响，发现站网密度增加到一定程度时，估算的流域累积面雨量趋于稳定，要充分测报流域降雨的空间分布不均匀性需要有一定的雨量站网密度，本文称此为临界雨量站网密度，在田头水流域为10个雨量站，即平均50 km2一个雨量站。雨量站网密度对流溪河模型参数自动优选结果的影响不明显，说明流溪河模型参数优选具有控制降雨空间分布不均匀性所带来的不确定性的效果。雨量站网密度达到临界值后，利用流溪河模型模拟洪水时的变化不大。

□

[1] 陈洋波,任启伟,徐会军,等.流溪河模型I:原理与方法[J].中山大学学报(自然科学版),2010,49(1):105-112.

[2] 陈洋波, 黄锋华, 徐会军,等. 流溪河模型Ⅱ:参数推求[J].中山大学学报(自然科学版), 2010,47(2), 95-102.

[3] A H Thiess.Climatological data for July,1911[J].Monthly Weather Review,1991.

[4] Drozdov D A, A A Sephelevskii. The theory of interpolation in a stochastic field of meteorological elements and its application to meteorological maps and network regionalization problems (in russian)[J]. Trudy NIU GUGMS l(18).

[5] Shepard D. A two-dimensional interpolation function for irregularly spaced data[C]∥ Proceedings of the 1968 ACM National Conference,1968:517-524.

[6] John C Davis. Statistics and data analysis in geology[M]. John Wiley and Sons, New York,1986.

[7] Christopher Daly. The prism approach to mapping precipitation and temperature[C]∥In proceedings 10th AMS Conference on Applied Climatology.American Meteorological Society:Reno,NV,20-23 October,1997:10-12.

[8] M F Hutchinson. Interpolation of rainfall data with thin plate smoothing splines - Part I: two dimensional smoothing of data with short range correlation[J]. Journal of Geographic Information and Decision Analysis,1998,2(2):139-151.

[9] 王名才.大气科学常用公式[M].北京:气象出版社,1994:518-519.

[10] Guillermo Q TabiosIII, Jose D Salas. A comparative analysis of techniques for spatial interpolation of precipitation[J]. Water Resources Bulletin,1985,21(3):365-380.

[11] 徐 晶,林 建,姚学祥,等.七大江河流域面雨量计算方法及应用[J]. 气象,2001,27(11):13-51.

[12] 毕宝贵,徐 晶,林 建. 面雨量计算方法及其在海河流域的应用[J]. 气象,2003,29(8):39-42.

[13] 朱求安,张万昌.流域水文模型中面雨量的空间插值[J]. 水土保持研究,2005,12(2).

[14] 王国庆,张建云,张 明,等. 雨量站网密度对不同气候区月径流模拟的影响[J]. 人民长江,2009,40(8):45-49.

[15] 阳 帆,王汉涛,黎晓东.雨量插值方法对BTOPMC模型及洪水模拟的影响[J]. 人民黄河,2012,34(5):16-19.

[16] 沈 冰,黄红虎.水文学原理[M].2版.北京:中国水利水电出版社,2005.

[17] 胡建华.赤溪水文站场次洪水降雨径流情况分析[J].广东水利水电,2008,(6):28-30.

[18] Yangbo Chen, Ji Li, and Huijun Xu. Improving flood forecasting capability of physically based distributed hydrological models by parameter optimization [J]. Hydrol. Earth Syst. Sci., 2016,20:1-18.