基于希尔伯特—黄变换的距离保护及其应用
2017-03-22张菁菁胡炎谢俊
张菁菁++胡炎++谢俊


摘 要距离保护作为电力系统的重要继电保护形式,对保证电力系统的安全稳定运行有着重要的意义。当电力系统发生故障时,故障暂态信号中的谐波分量与衰减直流分量对距离保护的准确性有着不利的影响,如何克服故障信号中暂态分量的影响成为提高距离保护可靠性的关键。本文提出了一种基于希尔伯特-黄变换的距离保护形式,利用希尔伯特-黄变换实现了故障信号中基频分量的提取,有效避免了故障暂态分量的影响,大大提高了距离保护的可靠性。
【关键词】希尔伯特-黄变换 距离保护 暂态分量
1 引言
近年来,随着我国电力系统的不断发展,电网规模不断扩张,对电力系统继电保护的可靠性提出了更高的要求。基于工频分量的距离保护作为电力系统继电保护的重要形式,对电力系统的安全稳定运行具有重要的意义,但其受衰减直流分量以及非整数次谐波分量的影响较大,基于这一不足,本文提出了一种基于希尔伯特-黄变换的距离保护形式,利用希尔伯特-黄变换实现了电力系统故障分量中基频分量的提出,对提高距离保护的可靠性与稳定有着重要的意义。
2 希爾伯特-黄变换在电力系统故障信号暂态分析中的应用
2.1 电力系统故障暂态信号的分析
当电力系统发生短路故障时,由于线路中存在电感等非阻性成分,故障电流中主要包括交流分量以及自由分量两大部分,相电流形式为:
其中第一项表示故障电流中的基频分量,第二项表示故障电流中的各次谐波分量,包括整数次以及非整数次谐波分量,第三项表示非周期的衰减直流分量,其形式为时间常数τ的指数衰减形式。通过上式可以看出,由于非周期衰减直流分量的存在,电力系统故障暂态电流并不对称,这就使得传统的傅里叶变换等基于周期信号模型的频谱分析手段难以有效应对。
2.2 电力系统故障暂态信号的希尔伯特-黄变换
希尔伯特-黄变换能够将复杂信号分解为多个固有模态函数以及一个单调余项,通过上式可以看出,电力系统故障暂态信号中的非周期衰减直流分量恰好是单调的余项,而其他项均可以表示为固有的模态函数,因此利用希尔伯特-黄变换可以将电力系统故障分量中的非周期衰减的指数函数项与其他项较好地分离,从而摒除故障分量中的非周期衰减直流分量,再通过希尔伯特变换就能够对其他项的幅值与相位进行求解,从而实现了信号中基频成分的提取,有效避免了谐波分量与非周期直流衰减分量的影响,对提高故障分量暂态分析的准确性有着重要的意义。
2.2.1 经验模态分解
利用希尔伯特-黄变换对电力系统故障暂态信号进行处理时,首先对信号进行经验模态分解,其大致过程为:首先求出信号的极大值点与极小值点,并利用三次样条函数对极大值与极小值点进行插值,构造信号的上包络线与下包络线,计算上下包络线的均值;其次对信号是否满足固有模态函数进行判断,若满足则利用希尔伯特-黄变换将其分解为若干个固有模态函数以及一个残余项,若不满足则返回上一步继续迭代;之后对分解得到的残余项继续执行前两步的操作,直至得到的残余项为单调信号或只存在一个极值点。希尔伯特-黄变换中经验模态分解的流程如图1所示。信号在迭代处理过程中得到电力系统故障暂态信号的各阶固有模态函数,包含信号中的基频分量以及整数次与非整数次谐波分量,而余项r则为故障暂态信号的非周期衰减直流分量,从而实现了暂态信号的经验模态分解。
2.2.2 希尔伯特变换
在完成经验模态分解后,电力系统故障暂态性被分解为若干固有模态函数以及非周期衰减分量,此时为了得到信号的基频分量,计算基频分量的幅值、相位等信息,还需要对经验模态分解得到的各界模态函数进行希尔伯特变换,对得到的希尔伯特谱进行分析。希尔伯特变换可以表示为:
其中,δ为积分的步长。
利用希尔伯特变换得到的希尔伯特谱,机选信号的瞬时幅值与相位:
进而可以得到信号的瞬时频率信息:
进一步计算信号的平均频率与平均幅值为:
最后根据初始相位与相位函数及频率函数间的关系,得到基频信号的初始相位值为:
3 基于希尔伯特-黄变换的距离保护及其应用
基于希尔伯特-黄变换在电力系统故障暂态信号分解中的优良性能,本文提出了基于希尔伯特-黄变换的距离保护方式:首先利用经验模式分解对电力系统的电压电流信号进行分解,并得到分解得到的各阶固有模态函数;其次利用希尔伯特变换对得到的各阶固有模态函数进行变换,计算固有模态函数的幅值与初始相位信息;最后利用信号中的基频信号计算测量阻抗,并判断测量阻抗是否在阈值范围内,从而判别区内区外故障,做出正确的动作。
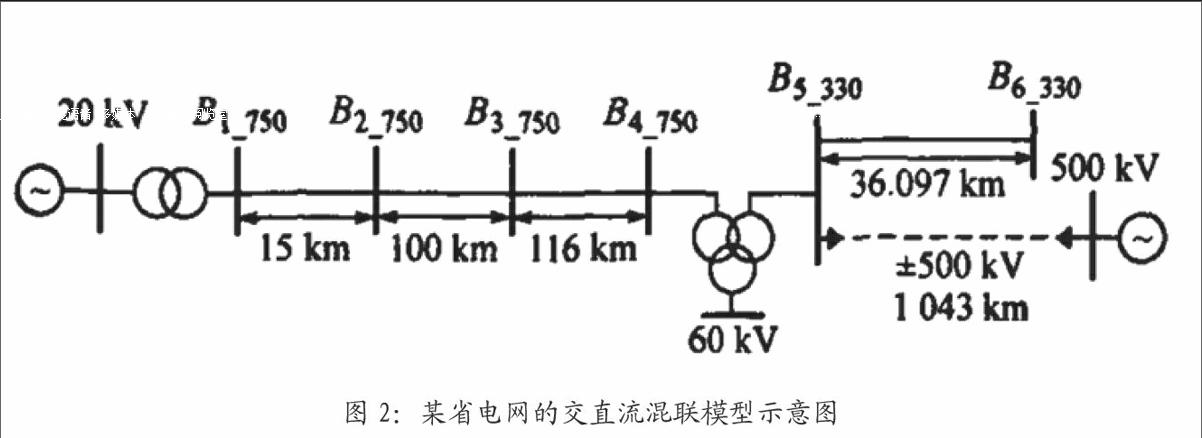
为了验证本文提出的基于希尔伯特-黄变换的距离保护的准确性与可靠性,选择某省电网的交直流混联模型作为仿真试验对象,其中500kV的直流输电线路与330kV的交流输电线路相连,对交流输电线路上的距离保护进行考量。
在选定试验模型中,由于交流系统与直流系统相连,导致线路电流中容易受到各次谐波的污染,尽管在正常运行时大部分谐波成分能够被滤波装置消除,但当系统发生故障时,残留的谐波成分在电压互感器的放大下会对故障电流、电压造成较大的影响。
通过表1可以看出,傅里叶变换由于受到非整数次谐波以及非周期衰减直流分量的影响,其故障测距误差较大,导致在本级线路末端发生故障时会发生超范围的动作情况,而本文提出的希尔伯特-黄变换有效克服了谐波及衰减直流分量的影响,测距精度得到了提高,距离保护的可靠性得到了较大的增强。
4 结论
希尔伯特-黄变换作为一种非线性非平稳信号的有效处理方式,本文将其运用在电力系统故障暂态信号的处理中,滤除了故障暂态信号中的非整数次谐波分量与非周期直流衰减分量,并提出了基于希尔伯特-黄变换的距离保护方式,通过仿真试验证明,其稳定性与可靠性均得到了较大的提高。
参考文献
[1]智慧,罗晓芬.有效滤除偶次谐波的改进半波傅里叶算法[J].继电器,2009,37(20):65-68.
[2]善文,汤宝平.Hilbert-Huang变换的滤波特性及其应用[J].重庆大学学报,2010,27(02):9-12.
[3]李天云,李楠.基于EMD的Hilbert变换应用于暂态信号分析[J].电力系统自动化,2011,29(04):49-52.
作者单位
1.上海交通大学电子信息与电气工程学院 上海市 200030
2.国网上海市区供电公司 上海市 200080
