土壤容重对蓄水坑灌入渗及水氮分布的影响
2017-03-21李京玲贾亚敏孙西欢
李京玲,贾亚敏,孙西欢
(太原理工大学水利科学与工程学院,太原 030024)
0 引 言
蓄水坑灌作为一种新型的节水灌溉方法,与地面灌溉相比,具有节水、保水、保肥、防止水土流失等优点[1]。利用蓄水坑灌法进行灌施时,肥液主要通过蓄水坑侧壁入渗,由于蓄水坑较深(20~60 cm),因此入渗过程中坑内水头变化较大。有研究表明,蓄水坑灌条件下,入渗水头在10~55 cm范围对第一时段末的入渗通量影响显著,而对入渗指数的影响不显著[2,3];灌水量对湿润锋运移、土壤含水率分布及硝态氮含量影响显著,而对铵态氮分布影响较小[4];肥液浓度对土壤水氮运移的影响不显著[4]。因此蓄水坑灌土壤水氮运移与入渗水头,灌施方式和土壤特性密切相关。受自然条件和耕作条件的影响,农田土壤容重的差异普遍存在,土壤容重作为反映土壤物理特性的重要指标之一,其对土壤的透气性、入渗性能和溶质迁移特性等都有显著影响[5,6],基于此国内外开展了大量有关土壤容重对节水灌溉条件下土壤水氮运移的影响研究[7-9],而有关土壤容重对蓄水坑灌土壤水氮运移影响方面的研究较少[10,11]。本文基于室内试验,探讨土壤容重对蓄水坑灌条件下土壤入渗、水分分布、铵态氮含量、硝态氮含量的影响,以期为蓄水坑灌法的推广应用提供理论依据。
1 试验材料与方法
1.1 试验装置
为研究土壤容重对蓄水坑灌入渗和土壤水氮运移的影响,试验采用自行研制的蓄水坑灌入渗物理模型(见图1)在室内进行了研究。试验土箱为一30°扇柱体,主体材料为10 mm厚有机玻璃,其规格为100 cm(半径)×120 cm(高)。蓄水坑安放在扇形的夹角处,规格为16 cm(半径)×60 cm (高),坑底为不透水形式。为防止在蓄水坑侧壁和土箱内壁的夹缝中出现优先流,试验过程中在蓄水坑侧壁均匀涂抹黄油,以保障夹缝密不透水。
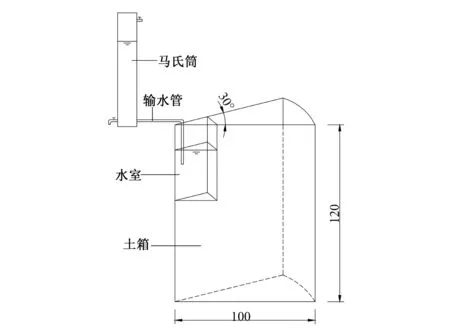
图1 蓄水坑灌入渗装置(单位:cm)
1.2 供试材料
供试土壤取自山西省太谷县北洸村苹果园20~120 cm土层,土壤质地为砂壤土,其土壤颗粒级配组成见表1所示。取回的土样经混合风干后测定,其基本理化性质为:初始体积含水率0.03 cm3/cm3,饱和体积含水率0.46 cm3/cm3,有机质含量1.1%,全氮含量0.068%,碱解氮含量148.9 mg/kg,铵态氮含量4.8 mg/kg,硝态氮含量58.8 mg/kg。

表1 供试土壤的颗粒级配组成表
1.3 试验方案
试验分别设置土壤容重为1.3、1.4、1.47 g/cm33个水平,灌水量为6 L,肥液浓度为700 mgN/L,肥料为尿素分析纯。试验过程中将风干后的土样按照一定的土壤容重分层装填进土箱,当装填高度到达60 cm时,在土箱的夹角处安放蓄水坑(图1中的水室),继续装填土样达土箱高度。灌施过程中控制水头于地表以下20 cm处,并采用马氏瓶进行恒定水位供水。
灌施结束后1 d,利用小型土钻分别在径向每间隔5 cm和垂向每间隔10 cm进行取土,直至湿润锋的边缘。取回的土样一部分采用烘干法测定土壤含水率[12]。另一部分装入带有标签的自封塑料袋冷藏,用于测定土壤氮素含量。土壤铵态氮和硝态氮含量按照土水比为1:10加入1 mol/L KCl溶液进行震荡浸提,并采用全自动流动分析仪(AA3,SEAL,德国)测定。
2 结果与分析
2.1 土壤容重对入渗能力的影响
图2为不同土壤容重下累积入渗量随时间的变化曲线。由图2可知,在入渗的140 min内,累积入渗量均随入渗时间的延长而增大,土壤容重越大,相同时间内的累积入渗量越小,不同土壤容重下肥液入渗能力的大小依次为:1.3 g/cm3>1.4 g/cm3>1.47 g/cm3。这是因为在土壤质地相同的条件下,随土壤容重的增大,土壤的紧实度增大,即单位体积土壤的密度增大,孔隙减小,孔隙尺度减小,孔隙弯曲程度增大,孔隙之间的连通性变差,导致单位水势梯度下水分通量减小,即土壤导水能力减小,相应的土壤入渗能力减小。
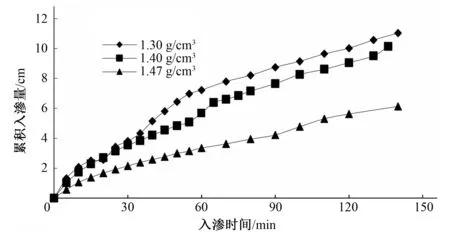
图2 不同土壤容重下累积入渗量随时间的变化曲线
经分析,不同土壤容重下累积入渗量I与入渗时间t的关系符合Kostiakov模型,即:
I=Ktα
(1)
式中:I为累积入渗量,cm;t为入渗时间,min;K为入渗系数,cm/min;α为入渗指数。
不同土壤容重下累积入渗量(I)与入渗时间(t)的拟合方程见表2。由表2可知,Kostiakov拟合方程中的入渗系数K和入渗指数α均随土壤容重的增大而减小。这进一步表明,容重越大,相应的土壤入渗能力越小,第一单位时间末的入渗率越小。对表1中的拟合方程进行显著性检验,取显著性水平为0.05,拟合方程中的决定系数R2均大于其临界相关系数rα(0.456),说明Kostiakov模型能很好地描述蓄水坑灌累积入渗量(I)随时间(t)的变化关系。

表2 不同容重下的累积入渗量拟合方程
2.2 土壤容重对含水率分布的影响
图3为r=20cm和r=35cm(r是指距离蓄水坑中心的径向距离)处不同土壤容重下体积含水率的分布图。湿润体20~60cm深度入渗界面范围,土壤体积含水率随容重的增大而增大。这与容重增大,单位体积总孔隙的数量增多有关。土壤湿润体范围随容重的增大而减小,土壤容重为1.30、1.40和1.47g/cm3时,其水平和垂直湿润距离分别为40、41、42cm和85、82.5、75cm,湿润范围的面积分别为2 669、2 615、2 472cm2。这与容重增大,土壤孔隙之间的连通性变差,土壤水分运动受土壤颗粒的阻力增大,导致运动范围减小有关。土壤容重越大,表层0~20cm湿润体范围土壤含水率越大,土壤水分向表层运移增加,而向下运移距离减小。这是因为土壤容重增大,土壤的孔隙尺度减小,土壤的毛管作用力使得土壤水分向表层运移增加。
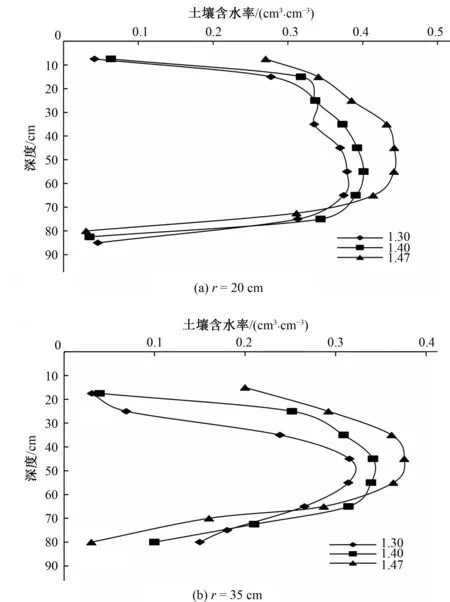
图3 不同土壤容重下体积含水率分布图
2.3 土壤容重对铵态氮分布的影响
图4为r=20cm和r=35cm处不同土壤容重下的铵态氮含量分布图。由图4(a)可知,在r=20cm径向距离处,由于吸附作用,土壤铵态氮主要分布在蓄水坑壁入渗界面附近,且在20~60cm深度范围内铵态氮含量随容重的增大而增大。这是尿素的水解和铵态氮的吸附共同作用的结果。由图4(b)可知,在远离蓄水坑壁的r=35cm处,土壤铵态氮含量随容重的增大先增大后减小,具体为1.4g/cm3>1.47g/cm3>1.3g/cm3。这是由于土壤容重增大,导致孔隙之间的连通性变差,土壤的通气状况不良,而尿素转化与通气状况和土壤含水率等有密切关系。
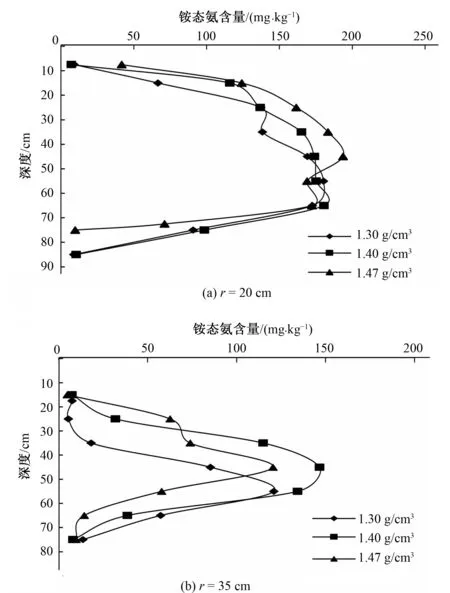
图4 不同土壤容重下铵态氮含量分布图
2.4 土壤容重对硝态氮分布的影响
图5为r=20cm和r=35cm处不同土壤容重下硝态氮含量分布图。不同土壤容重下,土壤硝态氮主要分布在湿润锋的边缘,蓄水坑壁入渗界面附近的硝态氮含量较低(有时低于本底值),这与硝态氮在土壤中容易随着水流的运动而运动有关。随土壤容重的增大,土壤硝态氮在深层湿润锋的累积增大,相对于1.3和1.4g/cm3,土壤容重为1.47g/cm3深层湿润锋处的硝态氮累积量分别增加了40.67%和11.34%。这是因为土壤中的硝态氮主要是通过铵态氮的硝化作用而增加,通过硝态氮的反硝化作用而损失,随土壤容重的增大,土壤通气状况变差,硝化作用减小,同时土壤容重的增大,导致土壤孔隙尺寸减小,土壤湿润锋处流速减小,硝态氮的累积增加。
3 结 语
(1)随土壤容重的增大,相同时间内的累积入渗量逐渐减小,不同土壤容重下的累积入渗量(I)与入渗时间(t)之间均符合Kostiakov模型。
(2)随土壤容重的增大,土壤湿润体范围逐渐减小。土壤水分再分布1d内,0~60cm深度范围土壤体积含水率随容重的增大而增大。
(3)不同容重下土壤铵态氮分布均表现出随径向距离的增加而减小。土壤铵态氮含量随土壤容重的增大在不同径向方向上变化不一致。
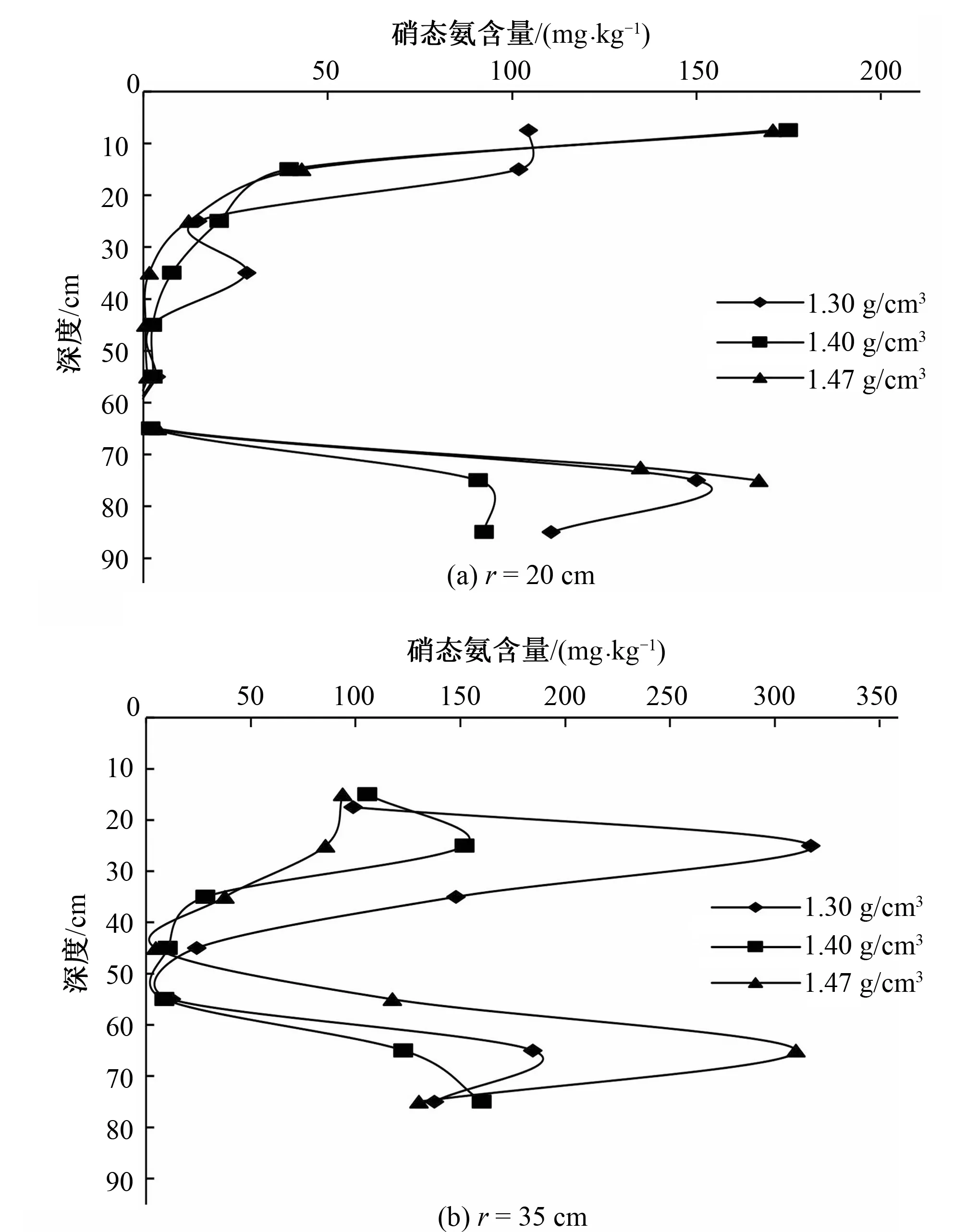
图5 不同土壤容重下硝态氮含量分布图
(4)不同容重下土壤硝态氮分布均表现出随径向距离的增加而增加,并在湿润锋边缘得到了累积。深层湿润锋处的硝态氮含量随土壤容重的增大而增大,相对于1.3和1.4g/cm3,土壤容重为1.47g/cm3深层湿润锋处的硝态氮累积量分别增加了40.67%和11.34%。
[1] 孙西欢.蓄水坑灌法及其水土保持作用[J].水土保持学报,2002,16(3):130-131.
[2] 马娟娟,孙西欢,李占斌.入渗水头对土壤水平一维入渗影响初探[J].水土保持通报,2005,25(2):20-22.
[3] 郭向红,孙西欢,马娟娟,等. 不同入渗水头条件下的Green-Ampt模型[J]. 农业工程学报,2010,26(3):64-68.
[4] 柴向斌.蓄水单坑水肥灌施条件下水氮运移分布规律试验研究[D].太原:太原理工大学,2011.
[5] 李 卓,吴普特,冯 浩,等.容重对土壤水分入渗能力影响模拟试验[J].农业工程学报,2009,25(6):40-45.
[6] 卢修元,魏新平,王君勤.土壤容重对溶质迁移过程的影响[J].水土保持通报,2013,33(2):26-29.
[7] 钟 韵,费良军,傅渝亮,等.土壤容重对浑水膜孔灌单点源自由入渗特性的影响[J].水土保持学报,2016,30(2):88-91.
[8] 脱云飞,费良军,董艳慧,等.土壤容重对膜孔灌水氮分布和运移转化的影响[J].农业工程学报,2009,25(2):6-11.
[9] 李 涛,张建丰,杨艳芬,等.土壤容重对深层坑渗灌入渗特性影响的试验研究[J].中国农业大学学报,2010,15( 6) : 89-94.
[10] 李京玲,孙西欢,马娟娟,等.蓄水坑灌单坑土壤水分运动模型的有限体积法求解[J].农业机械学报,2011,42(5):63-67.
[11] 李京玲,马娟娟,孙西欢,等.蓄水坑灌单坑土壤氮素迁移转化的数值模拟[J].农业工程学报,2012, 28(1):111-117.
[12] 龚振平. 土壤学与农作学[M].北京:水利水电出版社, 2009.
