宁夏引黄灌区土壤含水量蒙特卡洛方法检测的研究

2017-03-21赵伶俐王福平

节水灌溉 2017年8期

赵伶俐，王福平

(1.北方民族大学电气信息工程学院，银川 750021；2.北方民族大学创新创业教育中心，银川 750021)

0 引言

土壤含水量是水文、农业等领域衡量土壤干旱水平的重要指标，是植物生长状况的重要影响因素。宁夏引黄灌区是我国四大古老灌区之一，已有两千多年的灌溉历史[1]。宁夏引黄灌区位于黄河上游下河沿----石嘴山两水文站之间，南起青铜峡，北至石嘴山，包括吴忠、银川、贺兰等11个县(市)，沿黄河两岸地形呈“J”型带状分布[2]。土壤质地主要为灌淤土、盐渍土、淡灰钙土。宁夏引黄灌区地处中温带干旱区，属大陆性气候，干旱少雨、蒸发强烈，主要的灌溉用水来自黄河，农作物以水稻、小麦、玉米为主[3]。近年来，黄河来水偏少、春灌干旱少雨，如果灌溉中大灌大排则造成水资源浪费严重，水的利用率低，因此需要及时监测、准确了解土壤含水量，它是灌溉管理合理调配用水和农产量预报的重要参数，是农业节水灌溉、高效利用水资源的重要技术方法，对于区域农业生产及社会经济建设具有重要意义[4]。

土壤水分测量法先后提出烘干称重法、频域发射法、土壤水分遥测法等测量方法[5]。如何快速、有效、精确、低成本测定土壤含水量方法是研究者探索寻找的热点，视觉技术和人工智能结合是当前农业工程领域的热点研究之一，为土壤水分定量检测提供了一种新的技术思路。文中研究以宁夏引黄灌区为研究区，从室外采集土壤图像数据，基于图像处理和蒙特卡洛方法结合计算测量土壤含水量，并开展相关实验研究与实测土壤含水量的数据比较验证该方法的有效性，为土壤含水量检测和节水灌溉提供技术参考。

1 研究方法

1965年Bowers等[6]研究发现土壤光谱反射率在整个波长范围内随土壤水分的增加而降低，也即土壤图像中像素亮度值的深浅可反映土壤含水量的多少，但是土壤是由多种成分构成的复杂自然综合体，其图像特征会受到土壤本质，有机体，水分等多种复杂因素的影响，土壤图像灰度值与土壤含水量之间是一种非线性关系。由于土壤水分入渗空间变异性的存在，区域尺度范围的土壤入渗水分的测定往往需要由测点到测面的转化，其试验的工作量较大，对于这种非线性随机变化复杂的关系，利用土壤图像灰度测定土壤含水量需要建立一个能够比较完备表征土壤含水量的非线性模型。

蒙特卡洛方法是以统计理论为基础，通过对输入量Xi的PDF离散采样，由测量模型传播输入量的分布，计算获得输出量Y的PDF的离散采样值，进而由输出量的离散分布数值直接获取输出量的最佳估计值，该输出量的最佳估计值随PDF采样数增加得到改善[7]。

对随机输入量中的每一变量xi在(0，1)之间概率密度函数gx(ξ),通过测量模型传播求得输出量Y的概率密度函数PDF如式(1)所示。

(1)

基于图像处理和蒙特卡洛方法结合的土壤含水量检测技术路线如图1。

图1 蒙特卡洛法检测土壤含水量方法

1.1 材料和方法

本研究于2016年9-10月在宁夏贺兰县、永宁县、青铜峡和吴忠市等引黄灌区田间进行了实地调查与采样，选取了60个样本点。每个样本点圈定在900 m2左右的平整地块，选定的样地土壤类型和地表覆盖、植被状况接近。对样本点拍摄土壤表层图像，对采集的土壤图像进行处理，包括自适应中值滤波、几何校正、图像分割处理、提取土壤图像特征参数灰度平均值等[5]。在采集图像同时用联测LTH-6型土壤水分传感器[测量范围：0～50%(M3/M3),精度3%]测量0～20 cm的土壤样本含水量，所得数据为土壤含水量实测值。对实测土壤含水量数据进行编号记录，对采样点的土壤类型、表层植被状况和采样点的坐标位置进行定位并记录。对基于图像处理和蒙特卡洛方法结合所检测得土壤含水量值与实测土壤含水量值进行精度验证对比分析，评估检测方法的有效性。

文中土壤试验材料数据主要取自宁夏贺兰县立岗镇。软件是基于MATLAB用蒙特卡洛法测量土壤含水量和GS7.0地测软件分析土壤含水量空间分布。

1.2 测量模型的构建

设输入样本土壤图像灰度值为xi，i=1,…,l，xi∈R，对应的期望输出为土壤含水量值yi∈R，在高维空间构造最优线性估计函数：

y(x)=wTφ(x)+b

(2)

为了解决约束最优化问题，引入Lagrange函数：

(3)

土壤含水量传递函数的非线性回归问题转化为二次规划问题，根据Karush-Kuhn-Tucker条件，求解w,αi和b后，得到的最优分类函数如式(4)所示：

(4)

对非线性问题，可以通过非线性变换转化为某个高维空间中的线性问题，支持向量机通过定义核函数K(xi,xj)将这一问题转化到输入空间进行计算，选用核函数为高斯径向基函数：

(5)

估算模型函数可表达为式(6)所示：

(6)

即：

(7)

通过libsvm-mat参数寻优函数进行最优值寻找确定模型系数。

2 实验结果

2.1 土壤图像灰度的概率分布

在实验中首先对采集的土壤图像处理，计算图像灰度值，然后仿真分析输入量土壤图像灰度值的概率分布及其数字特征。在掌握各个输入量的相关信息即概率分布及其数字特征的基础上，得到各个输入量随机抽样的模拟值，进而由计算机计算出相应的输出量的模型值，进一步分析输出量的概率分布，这是蒙特卡洛法实施测量不确定度评定的基本原理和方法[8]。输入量的概率分布与模拟是实施蒙特卡洛法测量的关键一步。对随机采集的100个土壤图像样本处理，提取图像灰度值，根据对图像灰度值的分析，图2和图3是在MATLAB中仿真得土壤图像灰度值概率函数图形和直方图，服从正态分布N(178,1.5)的随机数。

图2 土壤图像灰度概率函数图形

图3 土壤图像灰度直方图

2.2 检测值与蒙特卡洛试验次数

构建了土壤含水量计算模型，输入量为土壤图像处理后的平均灰度值，输出值为土壤含水量，应用蒙特卡洛方法的过程中，减少了计算模型中一些附加的一阶或高阶灵敏度系数。当蒙特卡洛模拟次数越多，模拟结果的可靠性越高，测量结果的估计值越接近实际值，设定蒙特卡洛试验次数分别是200次，500次，1 000次，当蒙特卡洛试验次数不断增加，直至所需要的各种结果达到统计意义上的稳定[7]，输出值越精确。表1是蒙特卡洛试验次数1 000次，输出值样本中选取其中10个样本数据的土壤含水量。

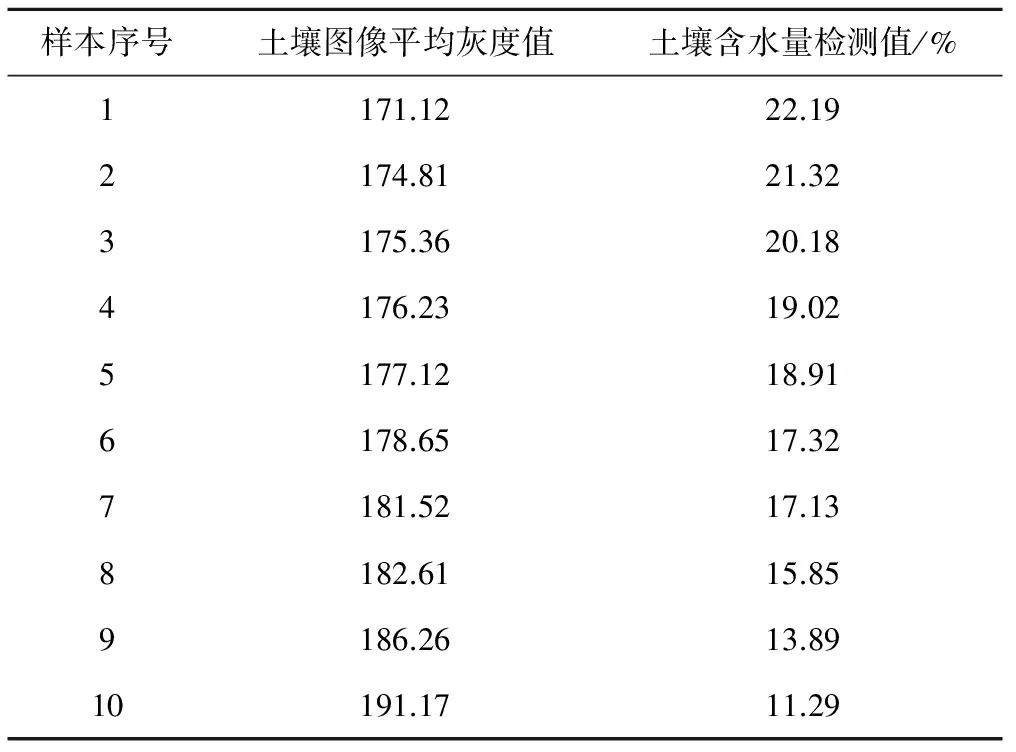
表1 土壤图像灰度值及土壤含水量

为了能够准确地实现土壤含水量的检测，需要评估验证蒙特卡洛方法和模型的精确性。以平均绝对误差公式和最大绝对误差公式作为性能指标评价模型的检测能力,说明模型的精确性。

平均绝对误差公式：

(8)

最大绝对误差公式：

(9)

表2是用联测LTH-6型土壤水分传感器[测量范围：0～50%(M3/M3),精度3%]测得土壤含水量数据(即实测值)与应用蒙特卡洛方法得出检测值之间的相对误差。从数据表格看出检测值和实测值之间的相对误差在6%之内，该方法模型具有精确性。

表2 土壤含水量检测值与实测值的相对误差 %

图4是蒙特卡洛模拟次数不同的测量值与实测值之间的精度实验结果对比。设定蒙特卡洛模拟次数分别是200次和1 000 次，计算土壤含水量检测值和实测土壤含水量进行对比。由图4仿真结果可看出在样本数据和蒙特卡洛模拟次数较少的情况下，土壤含水量检测值与实测值之间误差为4%～6%，随着蒙特卡洛模拟次数的增加，检测结果的可靠性越高，检测值和实测值之间误差越小，检测值越接近实际值。

图4 蒙特卡洛法模拟次数与实测值对比

2.3 土壤含水量空间分布比较

利用GS+地统计学软件，根据空间局部插值估计进行克里格插值制图，可以精确地了解土壤含水量的空间分布格局。图5是记录采集土壤样本点坐标位置，实测的土壤含水量数据进行克里格插值制图得到土壤含水量空间分布图。图6是记录采集土壤样本点坐标位置，利用图像处理和蒙特卡洛法估测的土壤含水量数据再进行克里格插值制图得到土壤含水量空间分布图。由土壤含水量的等值线图显示，两图的土壤含水量整体上分布走向一致，高值集中在测试区域的西北部分，土壤含水量达到16%～19%之间，测试区域的中间部分土壤含水量为13%～16%，低值主要分布在测试区域的西南部分，土壤含水量低于13%。在检测研究的部分区域出现误差，但误差小于3%，因此利用图像处理和蒙特卡洛方法检测土壤含水量方法具有精确性。