一维水流及溶质运移对VG模型参数的敏感性分析
2017-03-21高志鹏屈吉鸿陈南祥李五金华北水利水电大学资源与环境学院郑州450045
高志鹏,屈吉鸿,陈南祥,李五金(华北水利水电大学资源与环境学院,郑州 450045)
在自然界中,溶质运移在饱和、非饱和含水系统中广泛存在,非饱和带的水力参数对水分和溶质的运移具有较大的影响[1]。因此,研究非饱和土壤的水力参数对非饱和、非饱和-饱和含水系统中污染物的入渗影响是至关重要的,学者们通过大量理论和实验研究发现了土壤水分特征曲线,发现土壤水势与含水率之间存在着一定的规律性,但是不管是室内实验还是野外田间试验,测定土壤水分特征曲线均存在一定的局限性,为解决这一问题,国内外学者为此建立了经验与半经验理论模型[2],其中应用最广的是van Genuchten提出的计算土壤含水率的经验公式。非饱和土壤的水力参数控制含水率的分布,进而影响非饱和带溶质运移的过程[3]。
如今,采用VG模型研究非饱和带的水分和溶质运移的研究较多[4-8],而非饱和土壤的水力参数对溶质在非饱和含水系统中迁移规律影响的研究却比较少。Liu等通过研究变密度流下溶质在非饱和-饱和含水系统中迁移的规律,探讨了非饱和带主要水力参数(α、n、θr)对溶质穿透非饱和-饱和过渡带的影响,指出低含水率、中含水率、高含水率具有不同的影响规律[1]。Pan等采用基于方差分解的回归分析方法(The sample-based regression and decomposition methods)对影响非饱和带中水流及溶质运移的参数进行敏感性及相关性分析,研究分别对参数进行局部敏感性分析及全局敏感性分析,通过判定各个输入参数(van Genuchtenα、n等)对输出变量(渗流量、溶质通量等)的方差贡献率的大小,进而估计各个输入参数的重要程度[9]。王志涛等通过构建一维垂直入渗模型,采用单因素扰动分析法研究了VG模型中5个参数的扰动对垂直湿润距离和累计入渗量的影响[10]。
对非饱和带水分及溶质运移开展参数敏感性分析对于水资源管理、环境保护以及修复模式的提出均具有重大的意义。敏感性分析研究的是输入参数对输出结果的影响[11],包括局部敏感性分析和全局敏感性分析,局部敏感性分析评估了输出结果随某一个参数变化的过程,而全局敏感性分析则评估了输出结果随着多种输入参数变化而改变的过程,局部敏感性分析能直观的展现各参数对结果的影响程度,区分出重要参数及相对不重要参数,但是忽略了参数之间的相互影响;而全局敏感性分析则在考虑各参数间相互影响的条件下研究对输出结果的影响。目前国内对地下水数值模型的参数敏感性分析大都采用局部敏感性分析,典型做法是只改变一个参数值,观察其对模拟结果的影响程度,进而计算敏感度[12]。
卫河流域地处海河流域的南部,河南省的北部。卫河河水及沿岸地下水是流域内重要的淡水资源,水质的变化将影响到流域内人类生活和生态环境的稳定。卫河常年接收工业废水和生活污水,严重污染的河水通过包气带自由渗漏势必影响到地下水的水质。包气带是河水补给地下水必经的通道,因此研究包气带水力参数的扰动对水流及溶质运移的影响可以为卫河流域地下水保护、修复和治理提供理论基础。
本文以描述非饱和土壤水力特征的VG模型为理论基础,采用Hydrus-1d构建一维非饱和流数值模型,通过构建不同的情景模式,研究压力水头和NaCl浓度随深度的变化规律,探讨了VG模型参数对水流及溶质运移变化的敏感度大小。
1 模型的建立
1.1 Hydrus-1d模型简介
Hydrus-1d是美国农业部、美国盐碱实验室等机构开发出来的[13],是一种基于有限元的,可用来模拟一维变饱和度地下水流、根系吸水、溶质运移和热运移的计算机模型。模型可以处理各类复杂边界,包括定水头和变水头边界、定水头梯度边界、定流量边界、渗水边界、自由排水边界、大气边界等[14],同时具有灵活的输入输出功能,在土壤中水分运动、盐分、农药及土壤氮素运移方面得到了广泛应用[15]。
1.2 模型设置
模型模拟地下0~100 cm深度范围内的土壤,剖分1层,土壤类型采用软件提供的壤土(Loam),模拟时段为1 d,采用变时间步长输出模拟结果(0.4、0.8、1 d)。土壤水流模型采用van Genuchten-Mualem,不考虑水分滞后效应。水流模型上边界为定水头边界,边界水头值取为1 cm,下边界为自由排水边界。入渗过程中,湿润锋未达到下边界[20],故下边界可概化为定水头或隔水边界。溶质运移上边界为定浓度边界,为10 mg/L,下边界为零浓度梯度边界。
1.3 土壤水力函数方程
Hydrus-1d的土壤水力函数方程为van Genuchten-Mualem公式[16],其表达形式为:
K(h)=krKs
(1)
kr=θ1/2e[1-(1-θ1/me)m]2
(2)

(3)
θ=θr+θe(θs-θr)
(4)

(5)
式中:h为压力水头;kr为相对渗透系数;Ks为饱和导水率;θ为含水率;θs为饱和含水率;θr为残余含水率;θe为有效含水率;α、n为经验拟合参数;h<0表示包气带,h≥0表示饱和带。
1.4 水流模型
Hydrus-1d软件模拟土壤水分运动的方程为Richards方程[17],构建一维垂向均质非饱和入渗水流模型为:
(6)
式中:C(h)=dθ/dh,为容水度;K(h)为非饱和导水率;h为压力水头;z为垂向坐标,规定z向上为正;t为入渗时间;h0(z)为初始压力水头分布;L为入渗深度。
1.5 溶质运移模型
Cl-是公认的保守性离子,其在地下水中具有高溶解性而又难以被植物、细菌或土壤介质所吸收[18],因此选择NaCl为溶质运移的模拟对象。采用传统的对流-弥散方程(Convection-Dispersion Equation, CDE)来描述溶质运移的过程[19]。一维垂向溶质运移模型可描述为:
(7)
式中:C为NaCl浓度;θ为含水率;DL为纵向弥散系数;qz为垂向水分达西流速;L为运移深度。
1.6 情景设置
由式(1)~(5)可知,VG模型中共有θr、θs、α、n、Ks5个参数,以软件提供的壤土的经验参数值为基准参数(STD)构建模型,采用扰动分析法[21],将各参数在基准参数的基础上分别上下扰动5%、10%。模拟时,将某一个参数作一定的扰动而不改变其他参数,重新运行模型,得到各情景下压力水头和溶质浓度随深度的变化值。各情景设置见表1。
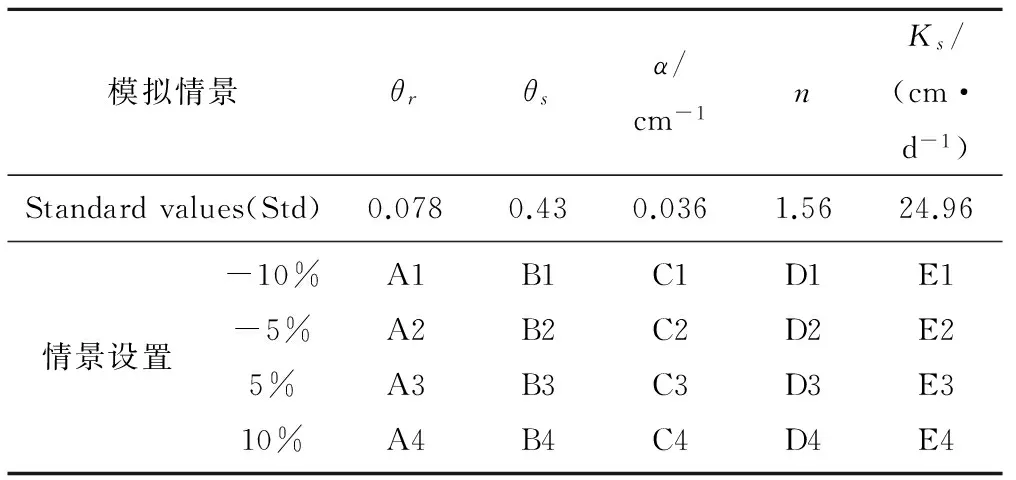
表1 模拟情景设置Tab.1 Situation modes
2 敏感性分析
2.1 敏感系数
敏感度分析是衡量改变一个因子时对其他变量影响的量,进行敏感度分析是为了确定模型的结果对模型参数的敏感程度,它将提供有关模型参数如何影响模拟结果不确定性的重要信息。如果模拟结果对某一特定参数高度敏感,那么模型做出重要解释和预报的能力将受到和该参数有关的不确定性的严重影响[22]。模型因变量对一个输入参数的敏感性是该因变量对该参数的偏微分[23]:
(8)

方程进一步标准化为量纲为一的形式为:
(9)
敏感度分析时,研究参数(如饱和渗透系数Ks)的变化多大(即饱和渗透系数的改变ΔKs/K0s)会引起数值解多大的变化(如模型变量压力水头的变化Δh)。给出某参数不同的扰动值(如ΔKs/K0s),通过计算压力水头的变化率Δh/h0或溶质浓度的变化率Δc/c0,然后绘制ΔKs/K0s和Δh/h0(Δc/c0)的关系曲线,则曲线的斜率即为敏感系数Xi,k。式(9)中Xi,k为正值时,表示y随ak的增大而增大;Xi,k为负时,表示表示y随ak的增大而减小。Xi,k大于1(或小于-1),表明输出变量的变化较研究参数的变化大,说明该参数对输出变量的影响较大。
2.2 敏感度指数
Xi,k的绝对值表示模型输入参数对模型输出变量的相对敏感性,或称敏感度指数。定义敏感度指数L为:
(11)
式中:m为观测点总数,本次取10;n为扰动次数,本次取4;Δi为扰动值(分别为-10%、-5%、5%、10%)。
上式定义的敏感度指数L为平均值,可以定量求得参数的敏感性,但是具有一定的粗糙性。
3 结果与分析
3.1 VG模型参数的扰动对水流及溶质运移的影响
3.1.1 θr扰动的影响
图1(a)和图1(b)为θr的扰动对压力水头的影响,图1分别表示了3个时刻(0.4 d、0.8 d、1.0 d)各扰动情景下压力水头随深度的变化规律。由图1(a)可以看出,θr的扰动对压力水头的影响较小(观察同一模拟期压力水头曲线所围面积,面积越大,影响越大),对湿润锋入渗深度的影响也很小,几乎可以忽略[22];从图1(b)可以看出,θr对压力水头的影响规律接近线性正相关,即敏感系数为正值,说明θr增大,压力水头也增大,并且随着入渗时间的推移,其影响程度呈先增大后减小的趋势;斜率小于1说明θr的影响较小。
图1(c)和图1(d)为θr的扰动对溶质运移的影响。从图1(c)可以看出,溶质浓度随深度的变化曲线在A1~A4情景下相对基准情景(STD)基本无变化,说明θr对溶质运移的影响非常小,几乎可以忽略;从图1(d)可以看出,其影响规律也接近线性正相关。


图1 θr扰动的影响Fig.1 Influence of disturbance of θr
3.1.2 θs扰动的影响
图2(a)和图2(b)为θs的扰动对压力水头的影响。由图2(a)可以看出θs对压力水头的影响与θr相比更大;B3、B4情景下θs较基准情景减小(即负扰动),湿润锋较基准情景(STD)下渗深度大,θs增大,B1、B2湿润锋较基准情景(STD)下渗深度小,说明θs对湿润锋具有较大的影响[10];其影响规律为非线性负相关,斜率为负,说明压力水头或湿润锋入渗深度随θs的增大而减小;且随着入渗时间的推移,其影响程度逐渐增大[图2(b)]。通常,饱和含水率(θs)与土壤的孔隙度相等,而土壤孔隙的多少,决定了岩土储水容水的能力,而孔隙的大小,对于岩土滞留、释出及传输水的能力影响很大[24],改变土壤的饱和含水率,相当于改变了土壤的储水、导水的能力,因此,对土壤的饱和含水率(θs)施加一定的扰动,对湿润锋的前进以及压力水头的影响会很大。
图2(c)和图2(d)为θs对溶质运移的影响。随着入渗时间的推移,土壤层上部饱和带的厚度逐渐增加(如0.4 d时0~20 cm深度,0.8 d时0~40 cm深度为饱和带),在湿润锋前进的前部则形成非饱和带,图2(c)表明θs的扰动对饱和带与非饱和带溶质的浓度随深度的变化均具有较大影响。从图2(d)可以看出θs对溶质运移的影响呈非线性负相关,且随着时间的推移,其影响呈先增大后减小的趋势。与对压力水头的影响相比,θs对溶质运移的影响正好相反,其负扰动的影响很大,而正扰动的影响则相对较小。
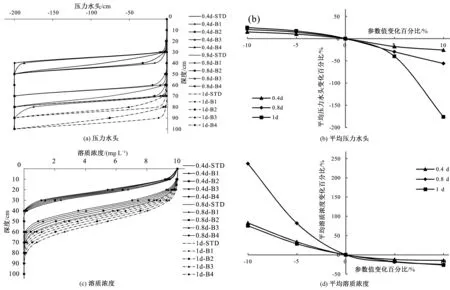
图2 θs扰动的影响Fig.2 Influence of disturbance of θs
3.1.3 α扰动的影响
图3(a)和图3(b)为α的扰动对压力水头的影响。从图3(a)可以看出α对压力水头和湿润锋的影响也较大,α的负扰动越大,湿润锋的下渗深度越大,α的正扰动越大,湿润锋的前进深度比基准情景的深度小10 cm左右,当α的扰动为-10%时,1 d时湿润锋甚至运移到了模型最底部;α对压力水头的影响也比较大,且其影响规律呈非线性负相关,与θs相同,α对压力水头的敏感系数也为负,说明α的增大伴随着压力水头和湿润锋入渗深度的减小[图3(b)]。
图3(c)和图3(d)为α的扰动对溶质运移的影响。由图3(c)可以看出α对溶质运移的影响相对较小,α的扰动不改变溶质浓度随深度变化的整体趋势,图3(d)表明α对溶质运移的影响规律为负相关,且负扰动为线性关系,正扰动为非线性关系。其敏感系数为负同样说明α的增大会引起溶质浓度的减小。
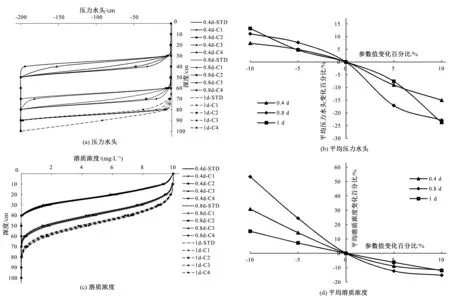
图3 α扰动的影响Fig.3 Influence of disturbance of α
3.1.4 n扰动的影响
图4(a)和图4(b)为n的扰动对压力水头的影响。从图4(a)可以看出,n对湿润锋和压力水头的影响也比较大,与α相反,n的正扰动会加快湿润锋的前进,负扰动则会减缓。图4(b)说明n对压力水头的影响规律为非线性正相关,随着入渗时间的推移其影响逐渐变大,负扰动对压力水头的影响比正扰动的影响大的多。
图4(c)和图4(d)为n的扰动对溶质运移的影响。从图4可以看出n对溶质运移的影响很大,其影响为非线性正相关。其对溶质浓度的影响与压力水头的影响正好相反,轻微的正扰动可能引起相当大的溶质浓度的波动,负扰动的影响则相对较小。
3.1.5 Ks扰动的影响
图5(a)和图5(b)为Ks的扰动对压力水头的影响。饱和渗透系数(Ks)可以定量说明土壤的渗透性能,渗透系数越大,岩石的渗透能力越强,图5(a)中饱和渗透系数越大(如1d-E1<1d-E2<1d-STD<1d-E3<1d-E4),相同深度处的压力水头越大,湿润锋下渗的深度也越大。Ks的扰动对压力水头的影响呈非线性正相关,且随着时间的推移,其影响程度也越来越大[图5(b)]。
图5(c)和图5(d)为Ks的扰动对溶质运移的影响。饱和渗透系数不仅对压力水头有较大的影响,因为其控制对流-弥散方程中的对流项,因此对溶质运移也具有较大的影响,如图5(c)和图5(d)所示,其影响规律为非线性正相关,与压力水头不同,Ks的正扰动的影响程度更大。
3.2 敏感性分析
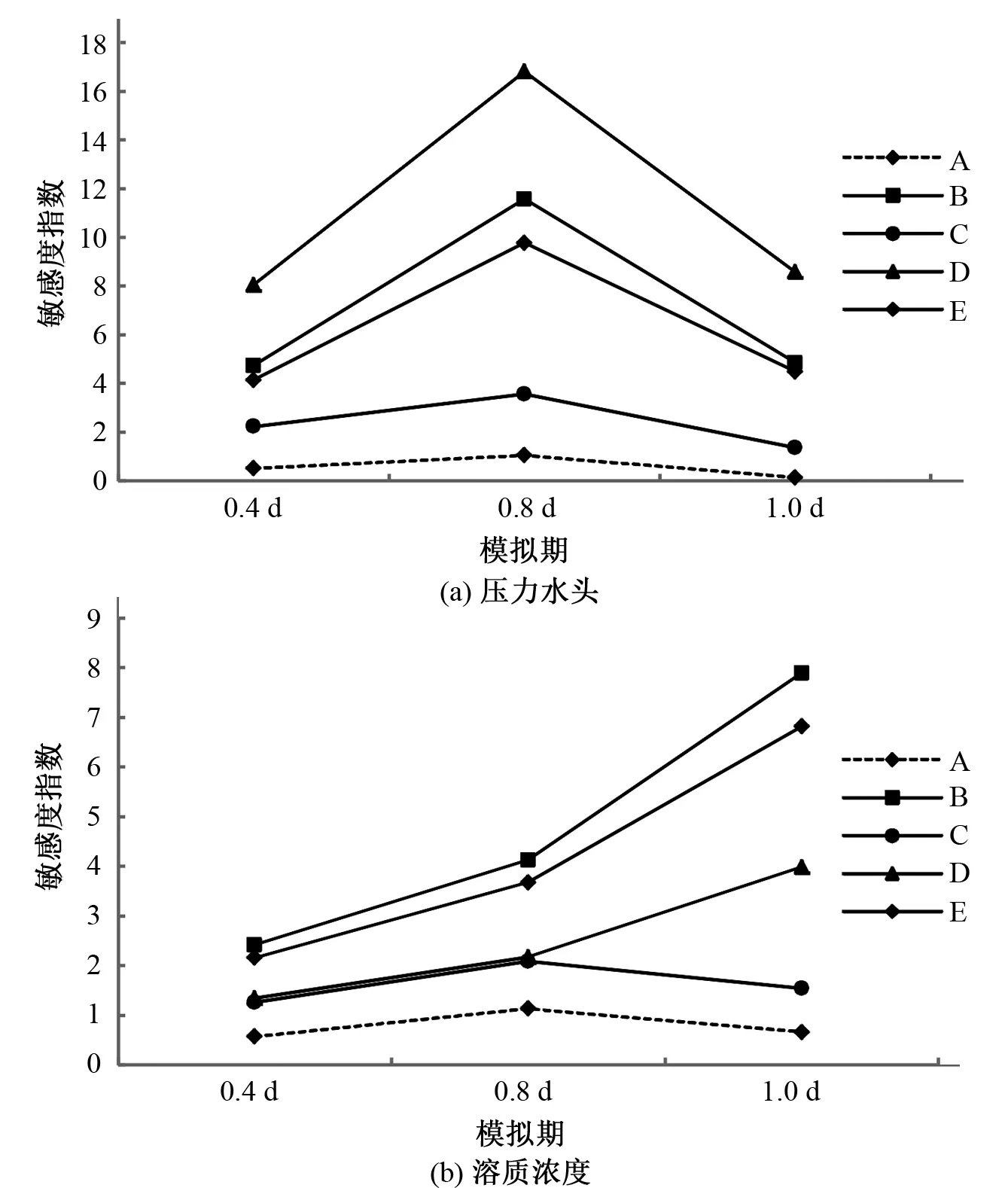
分别计算0.4 d、0.8 d、1.0 d时各参数对压力水头和溶质浓度的平均敏感度指数L,结果见图6。从图6可以看出各参数对压力水头的敏感度指数大小关系为:θr<α 图4 n扰动的影响Fig.4 Influence of disturbance of n 图5 Ks扰动的影响Fig.5 Influence of disturbance of Ks 图6 压力水头和溶质浓度对5个参数的敏感度Fig.6 The sensitivity of the pressure head and the solute concentration to the 5 parameters VG模型中θr、θs、α、n、Ks5个参数对模型输出变量的影响不尽相同,5个参数的扰动对压力水头和溶质运移的影响不仅呈现出不同的规律,其影响程度也随着模拟期的改变而变化。 (1)压力水头对5个参数的敏感度大小关系为:θr<α (2)溶质运移对5个参数的敏感度大小关系为:θr<α (3)据以上分析,采用数值模型研究污染河水对溶质运移的影响,应保证模型中敏感度高的水力参数的精度。θs、Ks、n的敏感度高且随模拟时间的增长对压力水头的影响呈上升趋势,α和θr的敏感度相对较低且对压力水头和溶质运移的影响均呈先上升后下降的趋势,故应保证θs、Ks、n的精度[10]。 [1] Liu Y,Kuang X X,Jiao J J,et al. Numerical study of variable-density flow and unsaturated-saturated porous media[J]. Journal of Contaminant Hydrology,2015,173:117-130. [2] 钱天伟,刘春国. 饱和-非饱和土壤污染物运移[M]. 北京:中国环境科学出版社,2007. [3] van Genuchten M T. A Closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of American Journal,1980,44(5):892-898. [4] Berlin M,Kumar G S,Nambi I M. Numerical modelling on transport of nitrogen from wastewater and fertilizer applied on paddy fields [J]. Ecological Modelling,2014,278:85-99. [5] Berg S J,Illman W A. Improved predictions of saturated and unsaturated zone drawdowns in a heterogeneous unconfined aquifer via transient hydraulic tomography:laboratory sandbox experiments[J]. Journal of Hydrology,2012,470-471:172-183. [6] 刘 超,何江涛,沈 杨,等. 非均质包气带三氮累积转化模拟砂箱试验[J]. 地学前缘,2012,19(6):236-242. [7] 庞雅婕,刘长礼,王翠玲,等. 某化工厂废液CODCr在包气带中的迁移规律及数值模拟[J]. 水文地质工程地质,2013,40(3):115-120. [8] 丁素玲. 非均质包气带中“三氮”迁移转化数值模拟[D]. 北京:中国地质大学,2012. [9] Pan F,Zhu J T,Ye M,et al. Sensitivity analysis of unsaturated flow and contaminant transport with correlated parameters[J]. Journal of Hydrology,2011,397:238-249. [10] 王志涛,缴锡云,韩红亮,等. 土壤垂直一维入渗对VG模型参数的敏感性分析[J]. 河海大学学报(自然科学版),2013,41(1):80-84. [11] Jacques J, Lavergne C, Devictor N. Sensitivity analysis in presence of model uncertainty and correlated inputs[J]. Reliability Engineering & System Safety , 2006,91:1 126-1 134. [12] 李木子. 地下水环境影响评价数值模拟中的参数敏感性分析[D]. 北京:中国地质大学,2013. [13] 李 玮,何江涛,刘丽雅,等. Hydrus-1d软件在地下水污染风险评价中的应用[J]. 中国环境科学,2013,33(4):639-647. [14] 余根坚,黄介生,高占义. 基于Hydrus模型不同灌水模式下土壤水盐运移模拟[J]. 水利学报,2013,44(7):826-834. [15] 郝芳华,孙 雯,曾阿妍,等. Hydrus-1d模型对河套灌区不同施灌情景下氮素迁移的模拟[J]. 环境科学学报,2008,28(5):853-858. [16] Hsin-Chi J Lin,David R Richards ,Cary A Talbot,et al. FEMWATER:a three-dimensional finite element computer model for simulating density-dependent flow and transport in Variably Saturated Media Version 3.0[Z]. [17] ZHU Y,ZHA Y Y,TONG J X,et al. Method of coupling 1-D unsaturated flow with 3-D saturated flow on large scale[J]. Water Science and Engineering,2011,4(4):353-373. [18] 沈照理,朱宛华,钟佐燊. 水文地球化学基础[M]. 北京:地质出版社,1993. [19] 王小丹,凤 蔚,王文科,等. 基于 HYDRUS-1D模型模拟关中盆地氮在包气带中的迁移转化规律[J]. 地质调查与研究,2015,38(4):291-298,304. [20] 范严伟,赵文举,毕贵权. van Genuchten模型参数变化对土壤入渗特性的影响分析[J]. 中国农村水利水电,2016,(3):52-56. [21] 鲁程鹏,束龙仓,刘丽红,等. 基于灵敏度分析的地下水数值模拟经度适应性评价[J]. 河海大学学报(自然科学版),2010,38(1):26-30. [22] 薛禹群,谢春红. 地下水数值模拟[M]. 北京:科学出版社,2007. [23] Zheng C M,Bennett G D. 地下水污染物迁移模拟[M]. 北京:高等教育出版社,2009. [24] 张人权,梁 杏,靳孟贵,等. 水文地质学基础[M]. 北京:地质出版社,2011.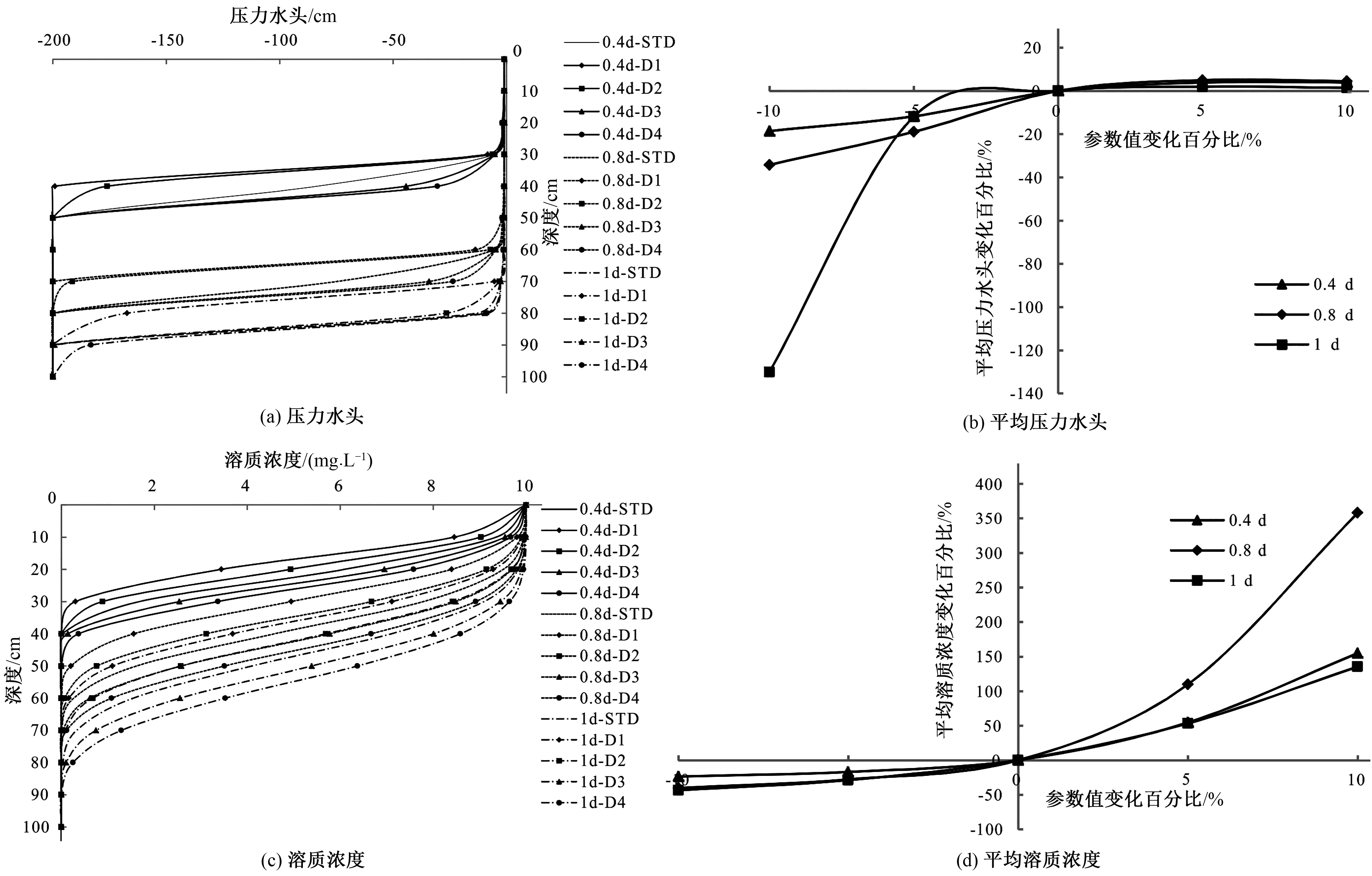

4 结 语
