Kostiakov入渗模型参数的预测精度对比分析研究

李昊哲，樊贵盛(太原理工大学水利科学与工程学院，太原 030024)

土壤的入渗是降水和地表水进入土壤转化为土壤水的过程，土壤入渗的能力受到土壤类型及其理化性质影响，而在灌溉过程中，土壤入渗能力影响灌溉水转换为土壤水的分布和速度，进而决定了灌溉质量与灌水效果[1]。所以，土壤水分入渗参数是确定灌水技术参数必不可少的重要依据。而在我国大部分农村地区都在沿用传统的地面灌溉方式，造成大量农业用水浪费，其主要原因就是缺乏合理的灌水技术参数。因此，精确获取土壤水分入渗参数已经成为节约灌溉用水和提高灌水利用率的关键。

由于水分在土壤中运动的复杂性，难以直接通过试验测定土壤入渗参数。现多利用土壤传输函数法，即建立以土壤常规理化参数为输入变量，土壤入渗参数为输出变量的土壤传递函数，来预测土壤入渗参数。很多国内外学者都用土壤传输函数预测了土壤特性参数和运动参数，如Vereecken[2]与Rawls[3]建立了以土壤特征水分曲线模型参数为输出变量的土壤传输函数，预测了土壤水分特征曲线。黄元仿[4]、J A Sobieraj[5]等通过建立土壤含水率与土壤其他理化性质间的函数，预测了不同含水率或基质势下的土壤水力传导度。同时，利用土壤传输函数来预测土壤水分入渗参数的成果也有很多，如冯宝平[6]引入BP神经网络对土壤水分入渗进行研究，得出了不同温度对土壤水分入渗的影响。郭华[7]建立非线性预报模型对Philip土壤水分入渗模型的参数进行了预测，得出用土壤常规理化参数可以对土壤水分入渗参数进行非线性预报可行的结论。岳海晶[8]基于大田土壤入渗试验，研究了土壤水分入渗时的结构变形对Kostiakov三参数入渗模型参数的影响，建立了线性预报模型，并得到了较精确的预测结果。

以上这些关于土壤传输函数的研究成果，是众多学者利用不同的土壤理化参数，建立不同的预报模型，因此也获取了不同的预测精度。而在有关土壤水分入渗参数预测的研究中，BP神经网络模型和支持向量机模型是目前较为常见的两种预测模型，本文分别利用这两种方法建立预测模型，利用相同的土壤基本理化参数对土壤水分入渗参数进行预测，并将预测结果的精度进行比较，并由此得出两种模型在预测土壤水分入渗参数时的不同特点。

1 材料与方法

1.1 土壤条件

本文中涉及的实验数据均得至在山西省进行的大田入渗试验，试验区北至大同市，南至运城市，均处于黄土高原，属大陆性半干旱季风气候，有气候干燥、日照充足的特点。同时由于试验区贯穿山西省全境，本文中所用的实验样本中涵盖了多种类型的土壤如棕壤土、褐土、黄绵土和黏土等，土壤质地与土壤结构也复杂多样。为更好地反映山西省黄土高原区农田土壤入渗特性，本试验在16个县区分别选取3～5个实验地点，进行大田土壤入渗试验，获取了大量的实验数据。

1.2 试验设备及试验方法

本次大田土壤入渗试验主要利用双套环入渗仪进行，其中外环直径60 cm，内环直径26 cm，内外环高度均为25 cm，下环达到犁底层，深度约20 cm。试验时为使内外环在同样的水位入渗，采用水位平衡装置保证内外环水位齐平。一般来说，土壤入渗试验达到稳渗状态的时间一般在60 min左右，本试验水分稳定入渗的时间取90 min，以确保试验成功。

本文中用于预测土壤水分入渗过程用到的土壤基本理化性质参数包括土壤体积含水率、土壤干容重、土壤质地以及土壤有机质含量。其中土壤含水率通过烘干称重法测得；土壤质地通过筛分曲线法获得；土壤干容重是利用蜡封法测定得到的；土壤有机质的测定采用重铬酸钾容量法。

1.3 Kostiakov二参数模型

为建立土壤传输函数，需先确立土壤入渗模型。根据达西定律这一入渗基本理论，国内外学者提出了众多土壤水分入渗的模型：如Richard方程、Philip模型、Kostiakov二参数模型、Kostiakov三参数模型等。

岳海晶[9]利用多元线性回归方法，建立了Kostiakov二参数、三参数入渗模型以及Philip入渗模型。预测结果证明3种预测模型都是可行的，但通过对3种模型参数预测的平均误差、预报参数下各入渗模型相对误差比较可以看出，Kostiakov二参数入渗模型各参数预报模型的精度高于三参数入渗模型以及Philip入渗模型。因此为获取更精确的土壤入渗参数，本文选用用Kostiakov二参数累积入渗量经验模型。

1.4 支持向量机与BP神经网络

人工神经网络是模拟生物神经网络对信息处理的方式，建立简单模型，对各类非线性信息进行处理。目前，人工神经网络已经在各个领域都解决了很多实际问题，表现出了良好的智能性。BP神经网络作为人工神经网络的一种在1986年被D Rumelhart和J McCelland引用于他们的著作中，并由此开始在各个领域被广泛应用。BP神经网络相对于其他人工神经网络模型，结构更简单、操作更简便、学习能力也更强，是目前应用最广泛的神经网络之一。

而支持向量机方法由Corinna Cortes和Vapnik于1995年提出，它建立在统计学习理论的VC维理论和结构风险最小原理基础上，可归结为求一个受约束的凸二次型规划问题，同时所得解为全局最优解。 与以往的回归问题算法相比，支持向量机有着数学推导严密、理论基础坚实、计算简便的优点，使它能广泛应用于分析数据，识别模式，解决函数拟合等问题。目前已经在气象预报、地下水位预测、图像处理等领域发挥了重要作用[10,11]。

2 结果与分析

2.1 试验样本的建立

相关研究表明，影响土壤水分入渗的主要因素为土壤体积含水率、土壤干容重、土壤质地、土壤有机质含量。因此，本文在结合前人研究成果的基础上选取土壤基本理化参数指标：0～10、10～20 cm土壤体积含水率θ0、θ1；0～10、10～20 cm土壤干容重γ0、γ1；0～20 cm土壤粉粒含量w1(0.05～0.002 mm)、黏粒含量w2(<0.002 mm)；土壤有机质含量G，即为本文的预测模型的输入因子，相应的Kostiakov二参数入渗模型的入渗系数k和入渗指数α为输出因子。

在确定输入、输出因子的基础上进行数据样本的建立。首先根据入渗试验数据，并结合Kostiakov二参数入渗模型，拟合得到入渗模型参数k和α，同时与其相应的土壤基本理化参数建立一一对应的关系，由此即可得到100组土壤基本理化参数与入渗模型参数间的对应关系如表1所示。

2.2 入渗参数预测精度比较

将上述建模样本分别输入到两预测模型中对两入渗参数进行预测，将预测结果与实测值进行对比分析，计算出两预测模型下入渗系数k和入渗指数α的相对误差值，结果如表2所示。

表1 建模样本表

表2 入渗参数相对误差比较表

从表2可以看出：支持向量机预测模型对入渗指数α进行预测的相对误差最大值为9.68%，最小值为2.25%，平均值为5.23%，对入渗系数k预测的相对误差最大值为6.82%，最小值为1.41%，平均值为5.23%；BP神经网络预测模型对入渗指数α进行预测的相对误差最大值为11.88%，最小值为1.27%，平均值为6.98%，对入渗系数k预测的相对误差最大值为10.57%，最小值为0.98%，平均值为4.70%，由此可以得到两预测模型的预测精度均在可接受的范围内，说明支持向量机预测模型与BP神经网络预测模型均能实现对Kostiakov二参数入渗模型公式中两入渗参数的预测。

同时从表2我们还可以得出：支持向量机模型对两入渗参数预测结果的相对误差最大值和平均值均比BP神经网络预测模型要小，但预测结果的相对误差最小值比BP神经网络预测模型要大。

2.2.1 入渗系数k预测结果分析比较

利用支持向量机算法和BP神经网络算法对Kostiakov入渗模型的入渗系数k进行预测，得到100组试验数据对应的入渗系数k的预测值，将预测值与实测值相比较，计算其相对误差值，得到两种算法下入渗系数k的相对误差值，比较这两种算法下预测结果的相对误差，得到图1所示的相对误差比较图如下。

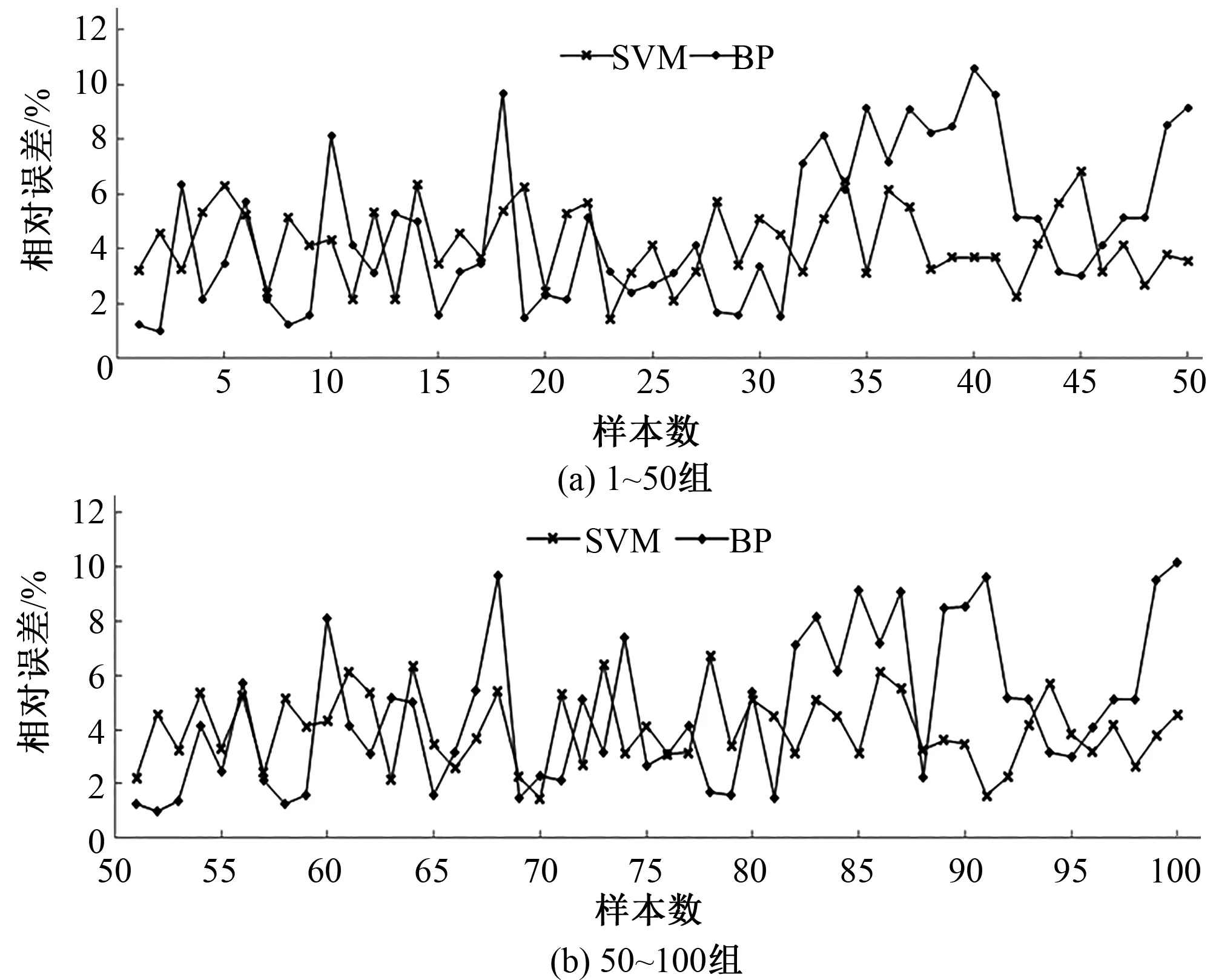
图1 1～100组入渗系数k相对误差比较图

从图1可以看出：支持向量机预测模型下入渗系数k的相对误差图较BP神经网络相对平稳，相对误差值的变化区间要小，相对误差值基本不存在小于2%或大于7%的值；BP神经网络预测模型下入渗系数k的相对误差图波动较大，相对误差值的变化区间要大，相对误差值低至0.98%，高达10.57%。

2.2.2 入渗指数α预测结果分析比较

从图2可以看出：支持向量机预测模型下入渗指数α的相对误差图较BP神经网络相对平稳，相对误差值的变化区间要小，相对误差值基本都在3%～7%之间；BP神经网络预测模型下入渗指数α的相对误差图波动较大，相对误差值的变化区间要大，变化范围在1.27%～11.88%之间。

图2 1～100组入渗指数α相对误差比较图

综上所述，Kostiakov二参数入渗模型参数的相对误差比较图可以看出：采用支持向量机算法对Kostiakov二参数入渗模型参数进行预测时所得的相对误差值相对稳定，能保持在一个小范围内变化；而采用BP算法得到的相对误差值表现出时而较大，时而较小，预测结果的相对误差在控制的精度范围内跳动较大。由此，在采用支持向量机算法对Kostiakov二参数入渗模型参数进行预测时能保持较高的稳定性，预测值与实测值不会出现较大的差异；而采用BP神经网络算法进行预测时，所得预测值会在实测值附件较大的误差区间跳动，但预测误差值能保持在可接受的范围之内。

3 结 语

(1)以土壤体积含水率、干容重、黏粒含量、粉粒含量、有机质含量作为输入变量，Kostiakov二参数入渗模型参数为输出变量，利用MATLAB软件，采用支持向量机算法和BP算法进行了预测，预测结果的相对误差平均值都能控制在7%以下，实现了对Kostiakov二参数入渗模型参数的预测。

(2)以Kostiakov二参数入渗模型参数为预测对象，以土壤基本理化参数为输入变量，采用支持向量机算法与BP算法相比，支持向量机预测模型所得预测结果的相对误差最大值和平均值要小，相对误差的最小值要大；同时，从所有预测样本的预测结果可以看出支持向量机算法具有比BP算法更高的精确度和稳定性。

(3)本文是建立在以Kostiakov二参数入渗模型为研究对象，以土壤基本理化为输入因子的基础上，针对大田入渗试验数据样本，利用支持向量机算法和BP算法进行的预测试验，并对两种算法下的预测结果进行分析比较，对于本次试验中所涉及的输入因子的选择、数据样本数的确定、精度指标的选择还有待进一步的完善。

[1] 雷志栋,杨诗秀,谢森传. 土壤水动力学[M]. 北京：清华大学出版社，1988.

[2] Vereecken H, Maes J, Feyen J, et al. Estimating the soil moisture retention characteristic from texture, bulk density, and carbon content [J]. Soil Science,1989,1489(6):389-403.

[3] Rawls W J, Brakensiek D L, Saxton K E. Estimation of soil water properties[J].Trans. ASAE,1982,25(5):1 316-1 320,1 328.

[4] 黄元仿,李韵株.土壤水力性质的估算----土壤转换函数[J].土壤学报,2002,39(4):517-523.

[5] Sobieraj J A, Elsenbeer H, Vertessy R A. Pedotransfer function for estimating saturated hydraulic conductivity: implications for modeling storm flow generation[J].Journal of Hydrology, 2001,251(3):202-220.

[6] 冯宝平,陈守伦.用BP网络预测温度对土壤水分入渗的影响[J].水利学报,2003,(2):6-8.

[7] 郭 华,樊贵盛. Philip入渗模型参数的非线性预报模型[J].节水灌溉,2016,(2):1-4.

[8] 岳海晶,樊贵盛.考虑土壤结构变形的备耕地入渗参数线性预报模型[J].太原理工大学学报,2015,(5):616-622.

[9] 岳海晶,樊贵盛.土壤入渗模型参数的多元线性预测模型精度的对比分析[J].灌溉排水学报,2016,35(10):73-77.

[10] 冯汉中,陈永义.处理非线性分类和回归问题的一种新方法Ⅱ:支持向量机方法在天气预报中的应用[J].应用气象学报, 2004,15(3):355-365.

[11] 王景雷,吴景社,孙景生,等.支持向量机在地下水位预报中的应用研究 [J].水利学报, 2003,(5):122-128.