判定地下水水动力弥散系数的综合分析法
2017-03-21陈素云
杜 川 ,陈素云,牛 耕
(1.北京市勘察设计研究院有限公司,北京 100038;2.北京市环境岩土工程技术研究中心,北京 100038)
0 引 言
随着环境污染问题的日益加重,地下水污染也愈发受到人们的关注。要对地下水污染进行合理评价与准确预测,就需要知道地下水水动力弥散系数这一重要的基础信息。目前,针对弥散系数的研究大多是基于野外弥散试验,一般方法是采用瞬时投源法或连续注入法向钻孔中投入示踪剂,测定示踪剂在含水层中的运移状况,根据所测浓度变化求得相关系数。
在研究地下水溶质运移的过程中,所求弥散系数的准确性会影响对地下水污染进行评价和预测的结果。关于水动力弥散系数的计算方法主要有直线图解法、标准曲线法配线法[1]、图解分析法和智能算法等。上述方法在实际应用中都有各自的优点,同时也存在一定程度的局限性。例如,忽略了含水层组分的不同、要求有两个及以上的监测井[2]、监测井要位于地下水主流线上等;同时,在小区域范围内由于地层分布的不均匀性,容易对流场和试验结果造成误判,从而影响求参的准确性。以往的弥散系数相关研究中,多是通过优化计算方法的思路进行求解,却忽略了不同试验方法及求解方法配合使用的优势,导致求参结果与实际情况存在一定程度的偏差等[3]。
结合区域水文地质条件,本文设计持续注入法和瞬时投源法两类弥散试验,并结合解析法与数值法分别求解,对比分析后确定合理的参数结果。
1 弥散试验及数学模型
弥散试验是指在稳定流场(天然或人工形成)内的投放孔中,瞬时或持续投放一定质量(浓度)的示踪剂,取投放时刻为流场中示踪剂浓度测定起始时刻,按试验设计要求的时间间隔测定观测孔中示踪剂浓度值,由此可以得到各个观测孔中示踪剂浓度随时间的变化过程。
其中,持续注入法通过在投源井和监测井之间形成水头差加速示踪剂随地下水流动,在水力坡度小的区域,有效避免了监测井需要布置在地下水主流线上的要求,且缩短试验时间、提高试验效率,对日常生产中污染物持续排入地下水的情况有较真实的反映;瞬时投源法排除了人工流场对含水层的扰动,通过天然流场的水力作用及弥散作用使示踪剂浓度变化,能更准确反映含水层的弥散系数[4]。
求解弥散系数时,数学模型的水文地质条件假设如下[5]:
(1)渗流区域是无限平面,且地下水流动是一维的,符合达西流速;
(2)示踪剂浓度的扩散为二维水动力弥散;
(3)多孔介质为均质、各向同性。
解析法充分依靠理论基础,在某些试验数据并不规律的情况下难以得出结果,且个别值会引起误判,搭配数值法针对不同的试验类型做综合分析,既可以弥补上述诸计算方法精度不足的问题,又充分利用了场区水文地质条件,能较好地反映含水层的弥散系数。
1.1 解析法
1.1.1 持续注入法
示踪剂投入方法采用持续注入法。设投源井为坐标原点,地下水流向为x轴方向,建立直角坐标系,适用于承压含水层中一维稳定流二维水动力弥散平面连续点源问题的解析解,计算公式如下[6]:
(2)

1.1.2 瞬时投源法
在地下水一维流场中,示踪剂瞬时投入[7]的二维弥散的求解公式为:
(3)
令x→0,y→0,即单井示踪剂弥散,代入上式:
(4)
式中:C(x,y,t)为t时刻区域上任意点处示踪剂的浓度,g/m3;DL为纵向弥散系数,m2/d;DT为横向弥散系数,m2/d;u为地下水平均流速,m/d;t为时间变量,d;n为含水层有效孔隙度,无量纲;m为单位含水层厚度上示踪剂瞬时投放质量,g/m。
1.2 数值法
根据研究区的具体条件,采用溶质运移模型进行模拟计算。如今在确定含水层的渗透系数、给水度等参数方面已较为成熟,因此在结合场区前期抽水试验、土工试验等现场工作获取的水文地质参数基础上建立的水流模型可信度较高,以此建立溶质运移模型,将上述两类弥散试验的示踪剂类型、投源井与监测井分布、投入方法等试验信息分别导入溶质运移模型,将模拟浓度结果与实测浓度结果进行拟合,通过不断调整模型的弥散系数确定最佳拟合曲线,进而得到场区弥散系数。
对场区渗透系数、含有对流、弥散和源汇项、一级动力学衰减作用的溶质运移可采用以下的微分方程的定解问题表示:
(5)
式中:Ω为渗流区域;C为污染组分浓度,mg/L;ui为3个方向地下水实际流速,m/d;Dij为水动力弥散张量的9个分量;R为阻滞因子,其值常大于1;C0为污染组分的初始浓度,mg/L;Γ1为一类边界;C1为类浓度边界值,即在该边界上浓度值已知,mg/L;Γ2为二类边界;fi为二类边界值,即通过该边界的溶质通量已知,mg/m2;qs为源汇项单位流量;Cs为源汇项溶质浓度;λ为一级反应系数。
水质模型是以水流模型为基础建立的,水质模型的概化与所建立的水流概念模型相符。
2 实例应用
试验场地位于北京市南部,场地内地形较平坦,目标含水层介质以卵砾石为主,试验区地下水类型为承压水,水位埋深23 m左右,年变幅较小,地下水天然流速0.08 m/d。含水层主要接受大气降水入渗和侧向径流补给,地下水径流条件较好,以侧向径流和人工开采为主要排泄方式。根据区域水文地质条件,设计“持续注入法”和“瞬时投源法”两组弥散试验。
在野外试验中理想的示踪剂是无毒、廉价、能随地下水移动、化学性质稳定且不被含水层介质吸附的物质,常用I、NaCl和荧光素等[8]。本次试验中采用氯离子作为示踪剂,测定地下水中的氯离子浓度和电导率,电导率用做校验。
2.1 持续注入法弥散试验
将按照一定浓度比例配置好的溶液,按照设定的流速持续注入投源井中,同时监测其他井的浓度变化。这样做的优点是可形成以投源井为中心向四周扩展的反降落漏斗,保证监测井位于地下水主流线上,以满足理论计算的要求。
在上游设置一个投源井DTW1,在下游设置一个监测井DTW2,监测井距离投源井1.77 m ,试验布置情况及试验区水文地质剖面见图1、图2。试验区地下水氯离子浓度本底值为170 mg/L。示踪剂溶液的持续注入时间1.5h,注入流速控制在0.05 m3/h。

图1 试验井布置示意图Fig.1 Diagrammatic sketch of test wells layout 注:图中地下水水位及流向均为试验过程中。

图2 试验区水文地质剖面示意图Fig.2 Diagrammatic sketch of hydrogeological section in test area
2.1.1 解析法
试验计算的基础参数见表1。

表1 持续注入法弥散试验基础数据Tab.1 Basic data of continuous injection diffusion test
注:根据试验过程中水位监测结果,结合达西定律,得到地下水渗透流速V=KI=7.64 m/d,地下水平均流速u=V/n=21.84 m/d=0.91 m/h。
监测井中氯离子浓度随时间变化曲线见图3。

图3 监测井示踪剂浓度变化曲线图 Fig.3 Tracer concentration variation curve of monitoring well
鉴于监测井中氯离子浓度增长明显时能较好反映弥散作用,因此选择图3中浓度呈现变大趋势时的A、B、C三点数据进行参数计算,解析法计算结果见表2。

表2 持续注入法弥散试验计算结果Tab.2 Calculation results of continuous injection dispersion test
从上述不同时刻的计算结果来看,氯离子浓度实测值与理论计算值的误差均在合理范围内,排除了个别数据不准确的问题。
2.1.2 数值法
结合抽水试验、颗分试验等前期水文地质勘查工作,获得含水层有关参数(见表3),并结合Visual Modflow软件针对试验区域构建水文地质概念模型,区域流场及试验区位置见图4。

表3 试验区含水层水文地质参数一览表Tab.3 Hydrogeological parameters of aquifer in experimental area

图4 区域流场及试验区位置图Fig.4 Regional flow field and location of test area
经过水流模型的识别、验证后 ,建立溶质运移模型并运行,为适应模型功能,将试验区氯离子浓度本底值统一设定为0 mg/L,同样对实际监测值做对应相减。由于监测井氯离子浓度从开始上升到达到峰值阶段能更好反映人工流场状态下溶质运移情况,因此对监测井处于该阶段的实测浓度与模拟浓度进行曲线拟合(见图5),按照误差平方和最小原则确定最优弥散系数。150 min时试验区地下水氯离子浓度分布情况见图6。

图5 监测井实测浓度与模拟浓度拟合曲线图Fig.5 Fitting curve of measured concentration and simulated concentration in monitoring well

图6 150 min时试验区地下水氯离子浓度分布图 Fig.6 Distribution of chloride ion concentration in groundwater at 150 min in test area
解析法和数值法求参结果对比见表4。

表4 解析法和数值法求参结果表Tab.4 Parameter results of analytical method and numerical method
2.2 瞬时投源法弥散试验
将一定质量的示踪剂瞬时投入投源井中,并适当搅拌地下水使之加速溶解[9]。该试验类型避免了人工流场的影响,使示踪剂在天然流场和水动力弥散作用下运移,求参结果更能真实反映含水层性质。此次试验的基础参数见表5。

表5 瞬时投源法弥散试验基础数据Tab.5 Data base of transient injection dispersion test
2.2.1 解析法
根据误差平方和最小的原则,对氯离子理论计算浓度曲线与实测浓度曲线进行拟合,该拟合法包括了示踪剂弥散过程中的全部数据,在调参过程中不同时刻均为相同的弥散系数,保证了拟合过程中参数的一致性,同时减少了个别资料的偶然误差,提高了计算精度。通过不断调整纵向弥散系数DL和横向弥散系数DT,使理论曲线与实测曲线逐渐拟合,并根据曲线拟合程度及误差平方和确定计算最优参数,拟合结果见图7。

图7 理论计算浓度曲线与实测浓度曲线拟合图Fig.7 Fitting results of theoretical calculation concentration curve and measured concentration curve
根据上述最优曲线拟合结果,得纵向弥散系数DL=0.65,横向弥散系数DT=0.10。
2.2.2 数值法
瞬时投源法的溶质运移模型建立方式及含水层参数与2.1.2中模型相同,由于是瞬时投源后开始浓度监测,因此将模型中MW18井投入试剂并均匀后的浓度设定为该井所在格栅的初始浓度。模拟浓度变化曲线与实测浓度变化曲线拟合结果见图8。
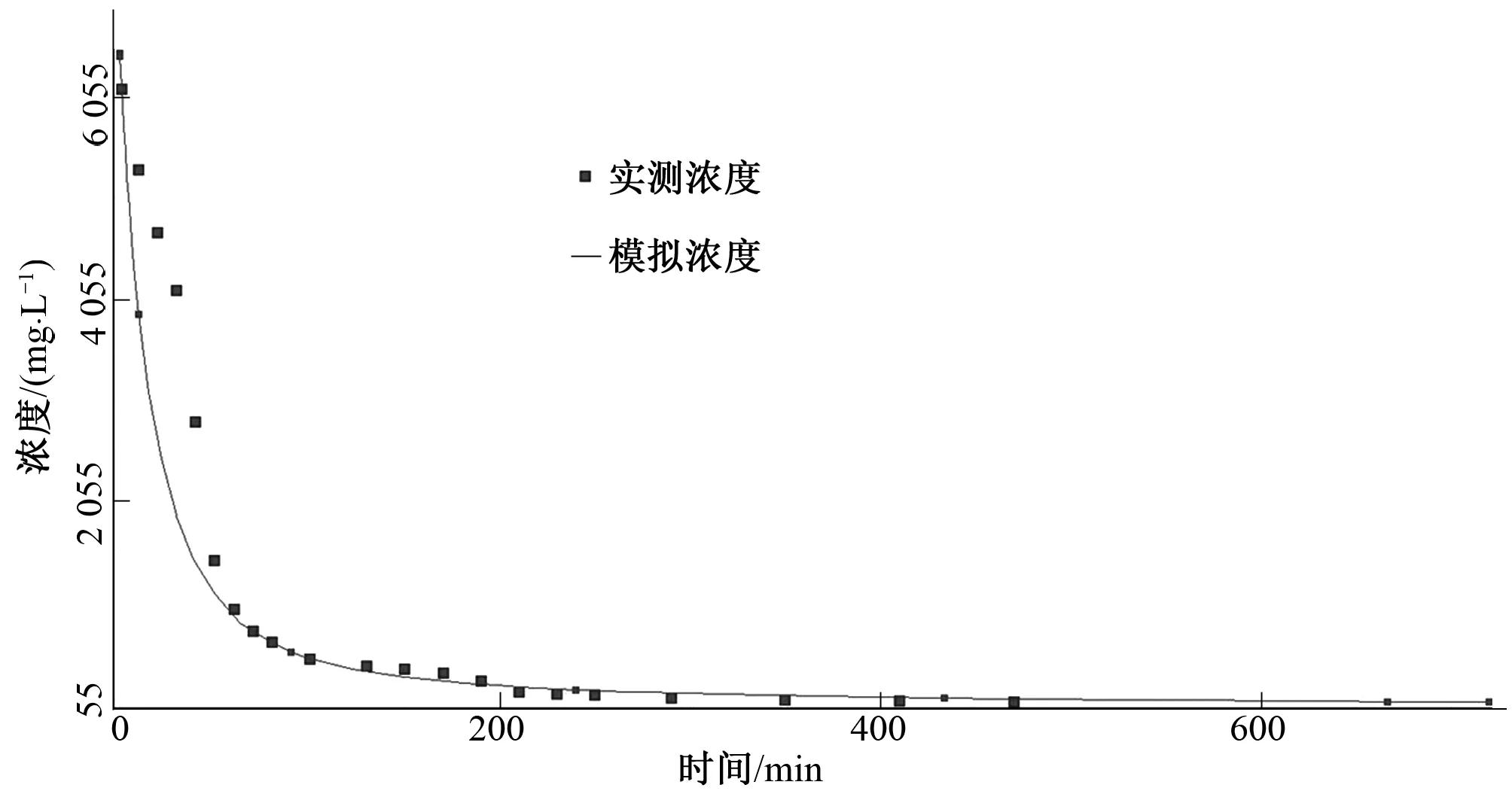
图8 实测浓度与模拟浓度拟合曲线图Fig.8 Fitting curve of measured concentration and simulated concentration
解析法和数值法求参结果对比见表6。

表6 解析法和数值法求参结果表Tab.6 Parameter results of analytic and numerical methods
2.3 结果分析
结合曲线拟合情况,大部分实际观测值在拟合曲线附近,从求参结果来看,所求纵、横向弥散系数均在合理的经验值范围内,两种试验类型下的纵向弥散系数差异较小,但持续注入法中所求横向弥散系数较瞬时投源法中偏大,考虑为在人工水头影响下,示踪剂横向弥散作用加强所致[10]。
3 结 语
本文在综合考虑研究区水文地质条件的基础上,分别通过持续注入法和瞬时投源法对介质单一的含水层进行弥散试验,结合解析法和数值法对试验区弥散系数进行求解,并得到以下结论。
(1)为避免单一试验类型求解参数时造成的结果不准确性,引入基于不同水力特征的试验类型进行参数求解,保证了弥散系数结果的客观性。其中,持续注入法中通过形成人工流场,确保了监测井位于地下水主流线上,而瞬时投源法又尽可能的利用天然流场反映水动力弥散作用[11]。
(2)单井试验解析法计算中提出的全程最优线拟合法充分利用整体数据,并可以剔除异常点,减少个别观测值不准确的问题,避免了主观影响,在保证实测浓度与理论计算浓度误差平方和最小、理论曲线与实测曲线拟合最优的情况下,准确、便捷的进行参数计算。
(3)使用数值法的前提是对研究区水文地质参数,如渗透系数、给水度、孔隙度、流场等有准确把握,而如今抽水试验、土工试验等技术已较为成熟,所得参数准确性较高,在此基础上构建的模型才能更真实的反映弥散作用并得到最切实的弥散系数。
(4)本次试验及数值模拟重点针对水平方向的二维弥散,投源井及监测井内示踪剂浓度垂向的分布、弥散作用等方面还需要以后通过更加完善的试验及方法加以改进。
通过上述不同试验类型和参数求解方法,确保了所求含水层弥散系数的唯一性和可靠性,并且两种试验方法均模拟了现实情况中跑、冒、滴、漏的连续点源污染物排放和地下含水层中含有固定污染源的情况,能较好地反映地下水水动力弥散作用,对今后开展地下水污染方面的各项工作提供了较好的参考作用。
□
[1] 刘兆昌.地下水系统的污染与控制[M].北京:中国环境科学出版社,1991.
[2] 吴耀国,沈照理,田春生,等.二维地下水动力弥散系数确定的优选法[J].勘察科学技术,1996,(2):14-16.
[3] 郭建青,王洪胜.分析二维水动力弥散试验数据的相关系数极值法[J].勘察科学技术,2001,(1):26-30.
[4] 蒙 璐,周志芳.野外单孔试验确定二维水动力弥散度[J].人民黄河,2012,34(9):61-62.
[5] 薛禹群.地下水动力学[M]. 2版. 北京:地质出版社,1997.
[6] HJ 610-2016,环境影响评价技术导则地下水环境[S].
[7] 胡德新.利用一个观测孔确定弥散系数[J].勘察科学技术,1995,(2):13-16.
[8] 范 飞,崔中兴,黄立新,等.野外二维弥散试验参数计算方法评述[J].勘察科学技术,2013,(2):1-10.
[9] 王运国,毕春玲,高秀清.地下水水动力弥散问题中弥散度的单孔确定方法研究[J].吉林地质,1991,6(2):50-60.
[10] Kozo Sato. Modeling of hydrodynamic dispersion and two-phase flow in the complex variable boundary element method[J]. Science Direct, 2003,192:4 425-4 438.
[11] Sidauruk P,Cheng A.H-D,Ouazar D. Ground Water Contaminant Source and Transport Parameter Identifica-tion by Correlation Coefficient Optimization[J].Ground Water, 1998,36(2):208-214.
