一种新的双足机器人模型设计与相关研究

谭鹤毅

(南充职业技术学院 信息与管理工程系，四川 南充 637000)

一种新的双足机器人模型设计与相关研究

谭鹤毅

(南充职业技术学院 信息与管理工程系，四川 南充 637000)

针对双足机器人最简模型在行走过程中出现摆动腿足部擦地的问题，提出了一种通过摆动腿膝关节弯曲达到摆动腿缩短的新模型;当摆动腿开始摆动时，摆动腿膝关节弯曲锁定，摆动腿缩短；当摆动腿摆动到最大位置时，膝关节解锁，摆动腿伸直再锁定，此后摆动腿回摆，系统变为直腿模型。采用脚后跟冲击控制，在摆动腿落地前，拖后的支撑腿与地面接触处施加一指向髋关节的瞬时冲击力，冲击力可以减小摆动腿着地时能量的损耗，同时驱动被动机器人向前行走;设计了迭代学习控制算法，找到极限环与不动点，实现不同给定期望步长跟踪的冲击力的计算;仿真结果表明，迭代学习控制可以有效的实现不同期望步长的跟踪，可以很快的找到机器人系统的不动点，通过收敛的相平面，得到稳定的极限环，保证了机器人行走过程稳定。

双足机器人模型；冲击控制；不动点；迭代学习控制

0 引言

机器人是近年来快速发展的综合学科，是目前最热门的研究领域之一。自从1969年，日本早稻田大学开发出第一台双足机器人后，机器人进入了“仿人”研发阶段，并催生出本田公司的ASIMO与索尼公司的QRIO，成为了双足机器人研发领域的典型代表和里程碑，这些机器人，均是依据ZMP理论与轨迹跟踪方法实现稳定性控制的[1]。传统的机器人，驱动力和稳定装置是在所有的关节均要设置的，这就致使机器人的构造、设计均很冗杂，机器本身的灵活性和能量利用率都很小，这就使得该种机器人不能执行和从事耗时长、任务重的任务[2-3]。被动行走概念是由加拿大学者T.McGeer于1989年首先提出，机器人可以仅靠自身重力势能作为能量输入就可以实现沿斜坡向下的稳定行走[4]。为了实现机器人在平面上的行走，设计出半被动机器人，就需要加入主动驱动控制。D.Kuo使用最简模型研究机器人在平面上的半被动行走，研究了能量消耗问题，以及速度和步长的关系，Kuo使用了两种控制驱动方式：摆动腿撞击前，支撑腿脚后跟作用一指向髋部的冲击力；在支撑腿髋关节上直接使用转矩控制。通过能量比较，得出脚后跟的冲力控制方法能量效率仅为髋关节直接转矩控制的四分之一[5]。

由于Kuo使用机器人最简模型在行走过程中，会出现摆动腿足部擦地的现象，为了避免这种现象，本文设计了一种通过摆动腿膝关节弯曲达到摆动腿缩短的模型，具体为：当摆动腿开始摆动时，摆动腿膝关节弯曲锁定，摆动腿缩短；当摆动腿摆动到最大位置时，膝关节解锁，摆动腿伸直再锁定，此后摆动腿回摆，系统变为直腿模型。

本文使用脚后跟冲击控制，具体方法：在摆动腿落地前，拖后的支撑腿与地面接触处施加一指向髋关节的瞬时冲击力，冲击力可以减小摆动腿着地时能量的损耗，同时驱动被动机器人向前行走。控制冲击力的大小，可以实现半被动机器人在平面上稳定行走。通过解析法找到系统初值估计，设计迭代学习控制算法，找到极限环与不动点，通过仿真实现不同给定期望步长跟踪的冲击力的计算。

1 双足机器人新模型的设计与分析

1.1 摆动腿弯曲模型设计与分析

本文选用机器人最简模型，质量集中于髋关节和足部，为了调整机器人行走的频率，髋关节加入弹簧，作用于摆动腿摆动过程中。l为机器人腿长，g为重力加速度，θ为垂直方向与支撑腿之间的夹角，φ为支撑腿与摆动腿之间的夹角。如图1所示，机器人在碰撞后瞬间，膝关节锁定，摆动腿弯曲，摆动腿在摆动过程中，使用弹簧转矩，建立系统的动力学方程：

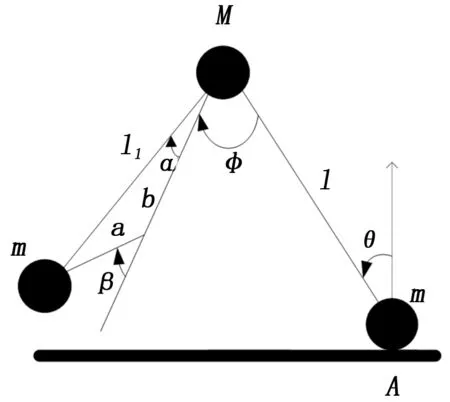
图1 摆动腿弯曲锁定模型

支撑腿：

Mglsinθ-mglsinθ-mgl1sin(θ+a-θ)=0

(1)

摆动腿：

(2)

支撑腿：

(3)

摆动腿：

(4)

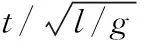
1.2 摆动腿伸直模型设计与分析

如图2所示，当摆动腿摆动到最高点时，膝关节解锁，摆动腿伸直再锁定，此时摆动腿弯曲状态机器人模型微分方程求解结束。如图3所示，当摆动腿回摆，系统进入直腿模型的微分方程的求解。

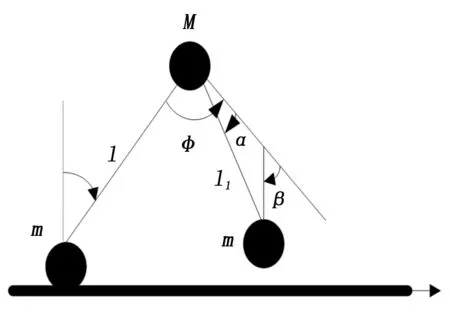
图2 摆动腿弯曲摆动到最高点

此时机器人系统的动力学方程为：

支撑腿：

(5)

摆动腿：

(6)

同上，无量纲化得：

支撑腿：

(7)

摆动腿：

(8)

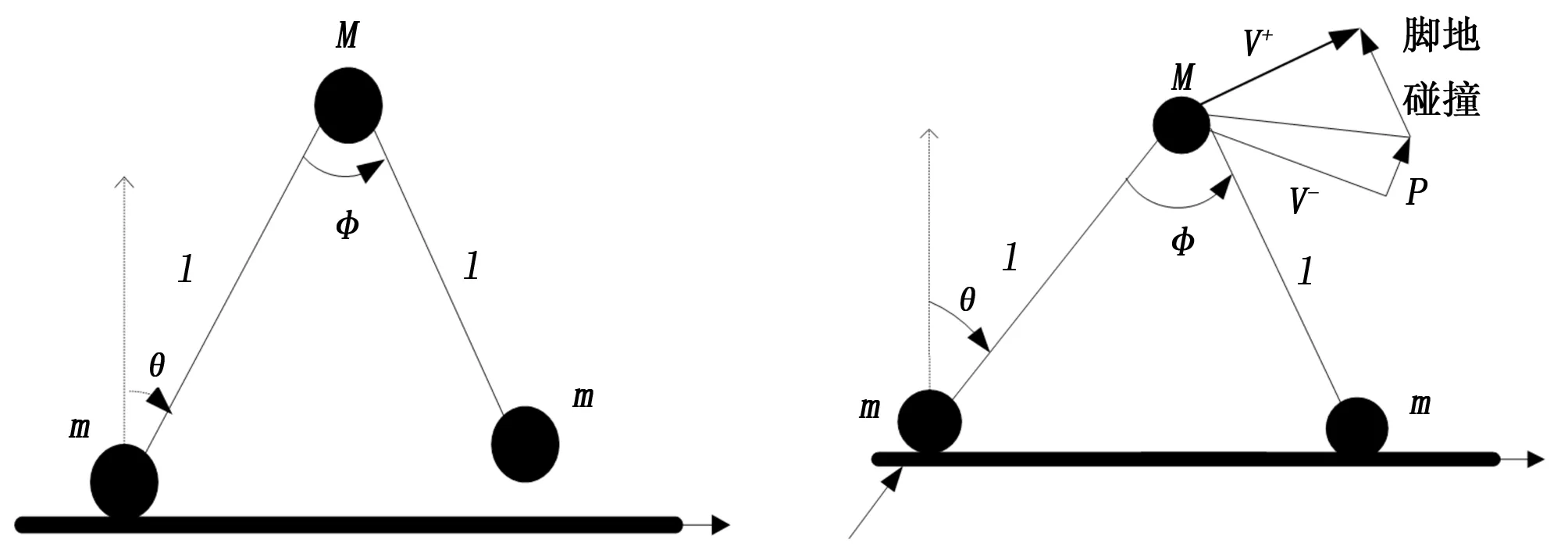
图3 摆动腿伸直锁定后直腿模型 图4 脚地碰撞理论模型

1.3 脚地碰撞切换设计与分析

机器人脚底与地面相碰接触之后，地面会施加给脚部足够强大的力的作用。碰撞过程中，机器人能量消耗，为了实现双足机器人在平面上的行走，必须提供驱动力，对其能量补充。如图所示，本文采用在脚地碰撞之前，使用脚后跟脉冲控制，具体方法：在摆动腿落地前，拖后的支撑腿处施加一指向髋关节的瞬时冲击力，冲击力可以减小摆动腿着地时能量的损耗，同时驱动被动机器人向前行走。控制冲击力的大小，可以实现半被动机器人在平面上稳定行走。

结合上面的模型，先假定在整个碰撞的环节，认为模型主体在位置上不发生改变，并且其腿和地面接触点之间满足角动量守恒定律；同时认为在碰撞过程发生之前，机器人的支撑腿相对于髋关节也满足角动量守恒的条件，附加规定机器人主体的各种速度能够进行不连续的改变。由前面的假设和规定，能够构建机器人主体在碰撞动作发生的前后瞬间具备的能量关系式，进一步求解可得：

(9)

(10)

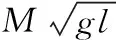
1.4 摆动腿弯曲缩短对摆动腿速度的影响

由于脚底碰撞后瞬间，摆动腿膝关节锁定，此时摆动腿缩短，根据摆动腿质心关于髋关节角动量守恒。可得膝关节锁定后，摆动腿角速度：

(11)

上角标与“+”与“-”分别代表膝关节锁定，摆动腿缩短前、后时刻的状态(假设摆动腿膝关节锁定对支撑腿的状态没有影响)。

2 机器人步态周期与极限环研究

为了使机器人周期性行走，机器人在每一个周期开始时的条件应等于系统初始时设定的条件。即满足：

(12)

当Km=0时，由式(3)、(4)、(7)、(8)可得线性化的近似方程：

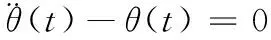
(13)

(14)

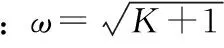
McGeer证明了极限环的存在和稳定性[6]。考虑脚后跟冲击力驱动，解析线性化近似的运动方程(12)、(13)， 结合碰撞切换方程(9)、(10)，代入边界条件(11)， 可得到极限环存在时，γ,ϖ,τ,ω,P必须满足以下方程:

(15)

(16)

(17)

如果给定频率ω值，由方程(15)可求的步态周期z的值。注意：利用方程(15)求τ时，可得τ的一个根为π/ω，这个根被称为“短周期”，此时得不到稳定的极限环。由于方程[]内非线性，无法求出解析解，可以使用数值方法计算方程的根。由于只关心最小根，所以可以使用Newton法求出(15)中“[]”内的最小根。将式(15)中得到的τ代入式(16)，由于γ给定，故可以求的初始ϖ的值，将给定步长γ，初始ϖ代入(17)式，就可以得到所需的脉冲驱动力P的初值。

稳定性能是衡量机器人功能的重要标准之一，如果驱动式机器人具备良好的稳定性能，说明该机器人在完成数个步态指令之后，机器主体在该相图中能够保证始终处在同一个环线之内，而不发生越位，这条环线就是理论上的稳定极限环[8]，它上面的初始点均具备稳定性，在动态系统理论里面起着重要作用。对于稳定极限环上面的稳定性求解问题，最基本的解法是按照庞加莱映射的理论步骤来计算[9-10]。庞加莱截面选择在脚地碰撞，膝关节锁定后，则一次庞加莱映射S(x)可表示为：

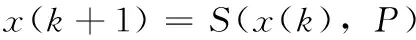
(18)

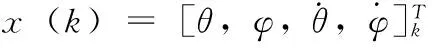
在动态系统理论里面，依据单个完整周期相对应的形态轨迹为研究对象和载体，文献[9]中所述的映射理论重点对周期内的形态轨迹进行了求解证明，在此基础上对回归映射做出了如下定义：x*=S(x*,P),由式(9)、(10)、(16)得一个周期极限环上，不动点的值都可以用支撑腿角度γ表示。同时，最简模型脚后跟冲击力P是影响不动点值的唯一因素。所以周期轨迹上，庞加莱映射可以表示为：

(19)

由于实际机器人系统Km≠0，线性化方程(13)、(14) 无法得到精确满足，实现理想步长跟踪的精确冲击力无法找到，系统存在误差。由于双足机器人行走具有周期重复特性，因此适合采用迭代学习控制，用于不断重复的同一轨迹的控制方法。作为学习控制理论的一个重要分支，迭代学习控制是一类全新的学习控制策略理论，具有极好的控制效果。该方法在解决控制性问题时，是通过不断校核控制律，确保有限时间内的实际轨迹与控制目标无误差，此外还必须满足快捷性的相关要求。使用该理论求解双足机器人的稳定性问题，具备很大的优势。首先具体要采用如下的P型闭环迭代学习控制规律：

(20)

其中,KP表示迭代学习因子，k表示离散时间变量，d表示期望值。e表示期望值与实际值之差，而第一周期的初始冲击力P的初始值采用(17)式估计。

3 仿真与分析

系统仿真流程图如下图5所示，在仿真中首先给定了ω的值(ω的值由弹簧弹性系数决定)，使用Newton法可以求出(15)中的步态周期τ，由于支撑腿期望角度γd给定，可以通过(16)，(17)式求的ω，P的初始值。设碰撞后膝关节锁定弯曲时的状态值为初值，将初值代入，设膝关节弯曲角度β=π/8，a=0.5,b=0.5,使用Runge-Kutta(RK4)法解弯腿模型微分方程(3)、(4)当检测到摆动腿的无量纲角速度为零时，微分方程(3)、(4)求解结束。将得到的状态值作为直腿模型的初值，使用RK4法解直腿模型的微分方程(7)、(8)当摆动腿的角度为支撑腿角度的2倍时，微分方程(7)、(8)求解结束，得到状态值。通过脉冲力控制、脚地碰撞、膝关节的弯曲锁定，得到下一个周期机器人运动的初始值。根据计算的得到的支撑腿角度与给定期望支撑腿角度间的误差，使用迭代学习控制，修正脉冲驱动力P的值。

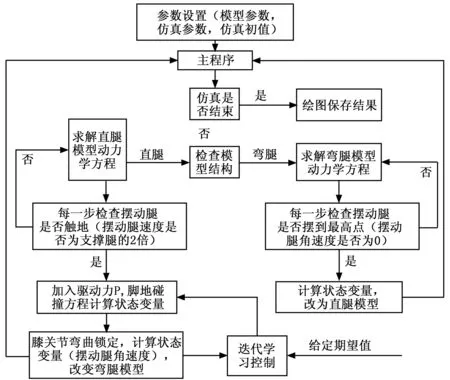
图5 机器人系统仿真程序流程图

设质量比Km=0.1，支撑腿初始值γ=π/8≈0.392 7，设机器人行走自然频率ω=2可以计算出冲击力P=0.239 8，仿真可得每一周期支撑腿的初始角度稳定在0.406 7，如图6虚线所示。误差由式(3)、(4)、(7)、(8)得线性化的近似方程(13)、(14)时产生。图6实线所示，通过户型迭代学习控制校正，可以实现给定理想角度的跟踪，设迭代学习因子KP=0.3，仿真可得支撑腿角度稳定在给定0.392 7，脉冲驱动力校正为P=0.222 6。

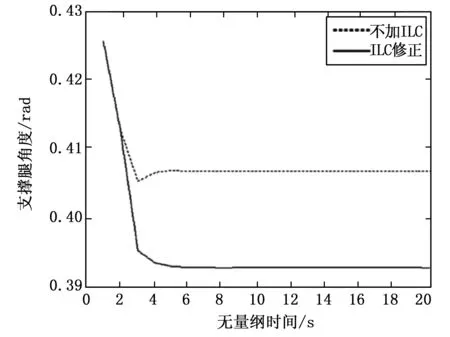
图6支撑腿在每一周期行走的初始角度

(ILC校正前后的比较，连续行走20个周期)

如图7所示，通过迭代学习控制冲击力P，可以实现支撑腿不同期望值的跟踪。

图7 支撑腿在每一周期的初始角度

(迭代学习因子KP= 0.3，质量比Km= 0.1，支撑腿初始值r=π/8≈0.392 7，机器人行走自然频率ω= 2，支撑腿期望值：γd=0.35，γd=0.42,连续行走20个周期)。

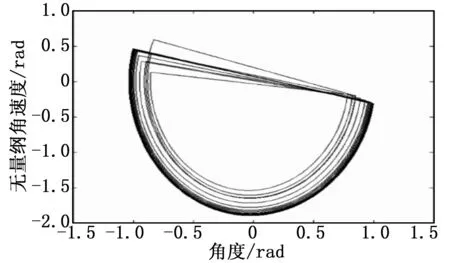
图8 摆动腿行走过程中的相平面轨迹

(迭代学习因子KP= 0.3，质量比Km= 0.1，支撑腿初始值r=π/8≈0.392 7，机器人行走自然频率ω= 2，支撑腿期望值：γd= 0.505，连续行走100个周期)。

图8所示为迭代学习控制机器人摆动腿相平面轨迹，可以看出，相平面轨迹很快的收敛到稳定的极限环，能够实现机器人的稳定行走。

4 结论

本文对最简行走模型进行了分析，研究了摆动腿加入膝关节弯曲缩短，以避免在摆动过程中摆动腿蹭地，在脚地碰撞前加入冲击力驱动控制，保证了机器人在平面上实现行走，同时极大提高了能量利用率。使用迭代学习控制冲击力的值，实现了给定期望步长(支撑腿角度)的跟踪。通过仿真结果，迭代学习控制可以有效地实现不同期望步长的跟踪，可以很快地找到机器人系统的不动点。通过收敛的相平面，得到稳定的极限环，机器人行走过程稳定。本研究对下一步实验设计被动行走机器人实物系统具有重要的指导意义。本文只通过仿真验证了系统极限环稳定性，关于极限环稳定性的严格证明也是下一步需要研究的问题。

[1] 谭 民, 王 硕. 机器人技术研究进展[J]. 自动化学报, 2013, 39(07): 963-972.

[2] 王斌锐, 冯伟博, 骆浩华, 等. 曲面上双足三自由度爬壁机器人设计与稳定性分析[J]. 机器人, 2014, 36(3): 349-354.

[3] 闵伟伟, 刘国栋. 基于 A* 算法的双足机器人足迹规划[J]. 计算机测量与控制, 2013, 21(01): 157-159.

[4] McGeer T. Passive dynamic walking [J].International Journal of Robotics Research,1990,19(1):62-82.

[5] Kuo A D. Energetics of actively powered locomotion using the simplest walking model [J].Journal of biomechanical engineering,2012,124(1):113-120.

[6] 成 钧, 廖世俊. 具有多个极限环非线性动力系统的解析近似[J].力学学报,2012,23(5):715-720.

[7] 刘丽梅,田彦涛,李建飞.被动行走机器人变路况切换控制[J]. 控制与决策,2011,26(8):1203-1208.

[8] 徐林森, 梅 涛, 宦 娟, 等. 双足机器人水上行走机理研究及推进机构设计[J]. 机器人, 2013, 35(3): 257-262.

[9] Idowu B A, Vincent U E, Njah A N. Synchronization of chaos in non-identical parametrically excited systems[J].Chaos, Solitons & Fractals,2013,39(5):2322-2331.

[10] Nikkhah M, Ashrafiuon H, Fahimi F. Robust control of underactuated bipeds using sliding modes[J].Robotica,2012, 25(03):367-374.

[11] 赵九洲, 居鹤华. 双足机器人步行动力学特性分析及简单仿生控制[J]. 计算机测量与控制, 2013, 12: 027.

[12] 敬成林, 朱晓铭. 双足机器人行走控制算法的三维仿真研究[J]. 计算机仿真, 2014, 31(3): 346-350.

A New Kind of Bipedal Robot Model Design and Related Research

Tan Heyi

(Information and Management Engineering Department, Nanchong Professional Technic College，Nanchong 637000, China)

When the simplest model of robot is in the process of walking, the feet of its swinging legs may brush the floor. In view of this problem, a model to shorten the swinging legs when the knees bend is proposed. When the swinging leg begins to swing, the knee of the swing leg bends and gets locked and the swing leg becomes shortened; when the swing leg swings to the largest position, the knee becomes unlocked and then locked after the swing leg unbends. In this condition, the swing leg swings back and the system becomes straight leg model. The heel impact control is adopted, so that before the swinging leg goes to the ground, an instantaneous wallop on to the hip can be applied at the place where the dragged support leg connect with the ground. The impact can reduce the energy loss of swinging leg landing on the ground, and can also drive the passive robot to walk forward. Iterative learning control algorithm is designed to find the limit cycle and the fixed point; through simulation, the impact forces under the tracking of different given expectation steps are calculated. The simulation results show that the iterative learning control can effectively implement the tracking of different expectation steps, quickly find the fixed points of robot system, and get a stable limit cycle through the convergence of the phase plane, to ensure the stable walking process of the robot.

bipedal robot model; impact control; fixed point;iterative learning control

2016-04-07；

2016-06-21。

谭鹤毅(1980-)，男，四川南充人，硕士，讲师，主要从事计算机软件与理论方向的研究。

1671-4598(2017)02-0189-04

10.16526/j.cnki.11-4762/tp.2017.02.052

TP273

A