一种提高国产ADC模块采样精度的方法

周永明，许进亮，王淑炜，王真真，张洪彬

(1.北京航天发射技术研究所，北京 100076； 2.北京宇航系统工程研究所，北京 100076)

一种提高国产ADC模块采样精度的方法

周永明1，许进亮1，王淑炜2，王真真1，张洪彬1

(1.北京航天发射技术研究所，北京 100076； 2.北京宇航系统工程研究所，北京 100076)

为解决武器装备自主可控问题，以国产的处理器和多通道模数转换器(ADC)为核心，设计了一种完全国产化的多通道模拟信号采集模块;由于目前国产模拟芯片特别是模数转换器的精度指标较差，造成模拟信号采集模块精度较低，实用性较差;为提高采样精度，首先在采样时采用递推平均滤波方法，抑制采集信号中的周期性干扰，降低采集的随机误差;其次，对预先测量的几组数值进行一元线性回归，据此对采样值进行最小二乘估计，降低采集的固有偏置误差和增益误差;试验结果表明，该多通道模拟信号采集模块可同时采集多路模拟信号，采样精度高，最大采集误差由0.8%降低到0.12%，并且该模块通道间一致性好，可靠性高，国产化率达到100%，在武器装备中有良好的应用前景。

提高;国产ADC;采样精度;递推平均滤波;最小二乘估计

0 引言

模拟采集模块作为模拟信号和数字信号之间的桥梁，在电子系统中发挥非常重要的作用，在国防工业领域也有非常大需求，比如雷达、电子对抗设备、军用通信设备等[1]。在某型号信息化发射平台中，需要采集系统压力、流量、位移等多种模拟量，并对采样精度有较高要求。随着近些年国内芯片产业的发展，利用国产芯片设计模拟采集模块，实现装备的自主可控成为可能。

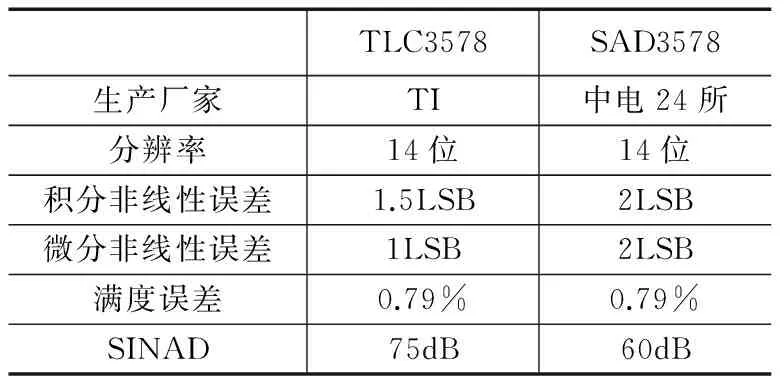
但是，目前国产模数转换器(ADC)的精度普遍不高，特别是能够同时完成多路模拟信号采集的ADC，精度指标较差。与进口ADC相比，国产ADC在非线性误差、信号与噪声加失真比(SINAD)等指标方面都有较大差距，表 1所示为可相互替代的进口14位ADC TLC3578和国产14位ADC SAD3578性能指标对比。根据公式(1)，利用SINAD估算两款ADC的有效位数(ENOB)分别为12.2位和9.7位，精度差别较大。

(1)

本文基于国产处理器和ADC，设计了一种完全国产、自主可控的多通道模拟信号采集模块，并采用递推平均滤波方法和最小二乘估计方法，大幅提高了模拟信号采集精度，对装备中类似模块具有较好的借鉴价值，有良好的应用前景。

1 硬件设计

为了避免模拟多路选择器的误差对系统误差造成影响，同时考虑电路的体积和成本，优先选择包含多个模拟通道的ADC，用单片ADC和对应的模拟调理电路来实现多通道模拟信号采集。模拟信号采集模块主要由模拟信号调理电路、模数转换电路、控制电路组成，系统框图如图1所示。

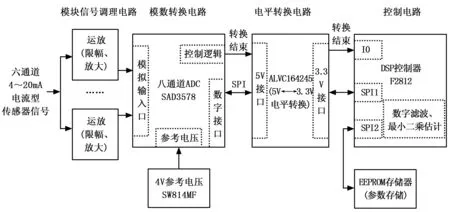
图1 系统组成框图

1.1 模拟调理电路

模拟调理电路将4～20 mA电流信号转换为电压信号，并将电压信号的幅值调整到合适的范围，以最大限度地利用ADC的满量程范围，降低采样误差。

模拟调理电路原理图如图2所示。调理运放选择749厂的低噪声高精度运算放大器F07，该运放失调电压仅为75 uV。由于运放输入阻抗无穷大，输入的4～20 mA电流仅流过200欧姆精密电阻，转换为0.8～4 V电压输入到运放同相输入端。经过运放放大，转换为1.6～8 V电压给ADC。模拟调理电路输出电压-输入电流关系为：

(2)

其中:IIN为输入电流(mA)，VO为模拟调理电路的输出电压(V)。

图2 模拟调理电路

1.2 模数转换电路

ADC选择中电24所的14位八通道ADCSAD3578，为目前国产最高分辨率的多通道ADC芯片。SAD3578是一种14位逐次逼近型电容结构ADC，该芯片模拟信号输入范围为-10～10V，最高工作时钟频率15MHz，最大采样率200KSPS，积分非线性误差最大为2LSB。该芯片非常适合数据采集和控制系统、雷达和导航系统[2]。

参考电压芯片选择中电24所专为SAD3578配套的参考电压芯片SW814，该芯片通过管脚编程，可以输出4V和2.5V参考电压，并具有噪声消除端，通过外接电容，可极大地改善电路的噪声特性。

模数转换电路如图 3所示。主要由SAD3578和参考电压芯片SW814组成。模拟输入端接入模拟调理电路输出的六路模拟信号，第7、8路分别接模拟地和8V参考电压，方便实现在线精度校正。控制端与控制器通过SPI接口相连，接收控制器的控制指令，完成采集后通过EOC引脚通知控制电路并通过SPI接口上传采集数据。

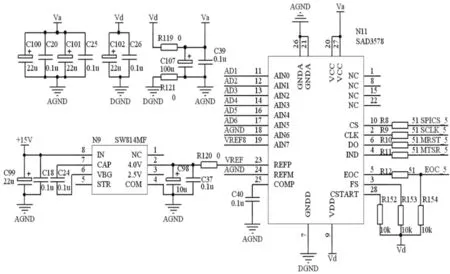
图3 模数转换电路

1.3 控制电路

控制电路的处理器芯片选择中电58所的DSP芯片JDSP320F2812，该芯片与TI公司的SMJ320F2812芯片兼容，硬件电路和软件开发均与SMJ320F2812相同，降低了开发门槛。该CPU是高性能的定点数字信号处理器，具有EV、高精度12位ADC、SCI、SPI、McBSP、CAN2.0等多种外设，广泛应用于各种控制领域。

DSP与SAD3578之间通过SPI接口传送指令和数据。SAD3578的IO为5V电平信号，而DSP的IO为3.3V电平信号，为保护DSP的IO引脚，在SAD3578和DSP之间用164245芯片设计电平转换电路。

2 软件设计

2.1 数据采集

SAD3578是8路14位串行输入输出的AD转换器，可以配置不同工作模式进行转换，本文使用单点转换模式，通过SPI接口配置ADC的采样参数，启动数据采样，读取采样数据。图4为采样M次6通道模拟量的软件流程图。

图4 多通道模拟信号采集流程图

上电后DSP处理器首先完成一系列初始化工作，包括DSP时钟初始化、SPI接口初始化、电平转换芯片JALVC164245使能和方向控制端的初始化以及SAD3578的初始化。

初始化完成后，依次进行各通道采样。SAD3578的数据采样由DSP通过SPI接口向其发送一个采集指令来启动，采集指令为16位控制字，前四位为采集的通道代号，分别为0～7，后12位为预留位，无具体功能。SAD3578接收到采集指令后，先进行采样，采样的时间由初始化时的配置位决定(长采样或短采样)。采样完成后进行模数转换，转换完成后转换结束引脚EOC由低电平变为高电平，DSP检测到转换结束标志后，向SAD3578发送下一条采集指令，同时接收上一次采集的数据。

SAD3578的采集数据左对齐，共14位，因此DSP接收到采集数据之后先右移两位，然后根据公式(2)和(3)转换为电压值和电流值。

(3)

(4)

其中:VO为采集的输入电压值，单位为V，Is为采集的电流值，单位为mA。

2.2 软件滤波

利用2.1节所述采集各通道数据，绘图分析多次采样数据的分布直方图，图 5所示为输入电流12mA时，1 000次采样数据的分布直方图，基本符合均值为12.037，标准差为0.014 4的正态分布。从图5中可以看出，当输入恒定电流时，多次采样值中包含随机误差。

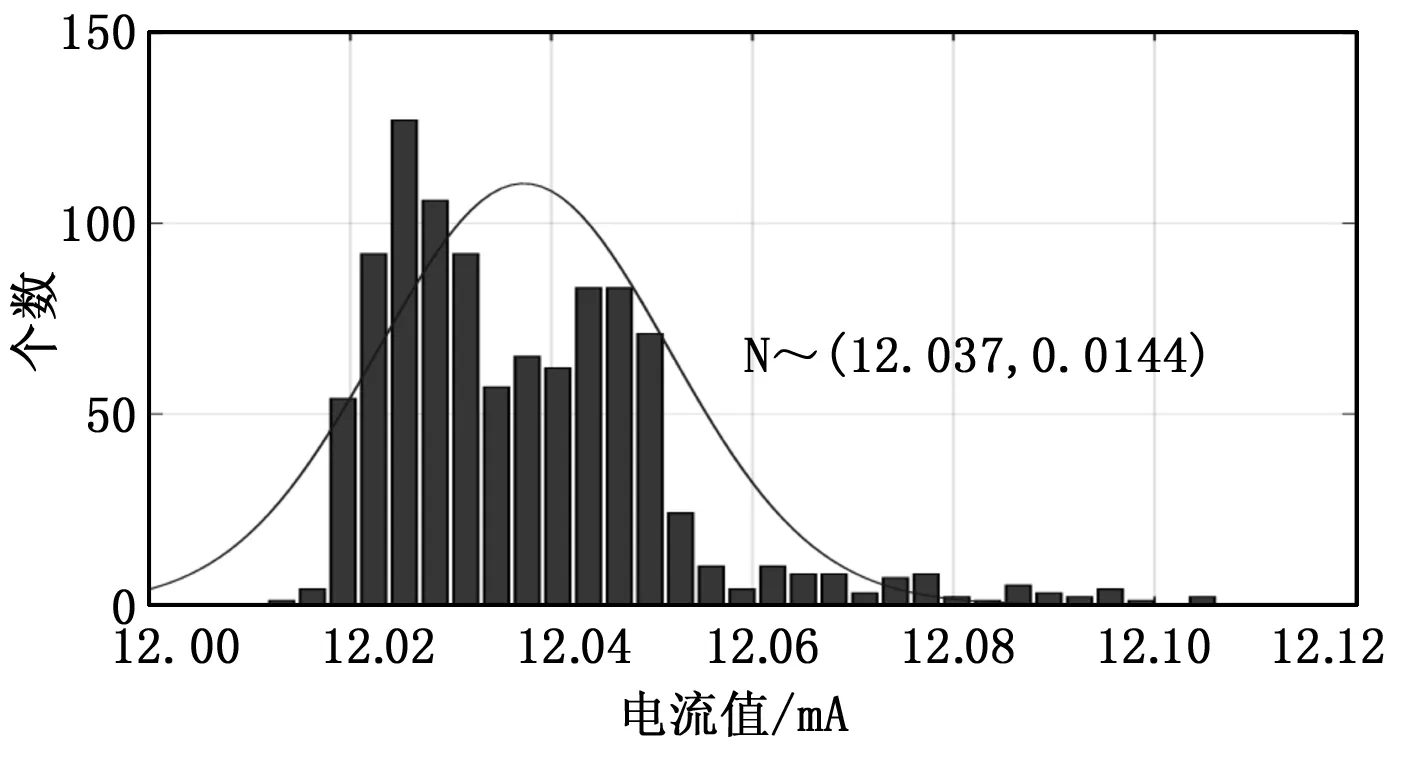
图5 输入电流12 mA时，1 000次采样数据的分布直方图

为减小采集的随机误差，消除信号抖动影响，在软件上采取多次采样，去除最大值和最小值，然后递推平均滤波的方法，抑制采集信号中的周期性干扰。采样结果的计算公式如公式(5)所示:

(5)

其中:i为滤波后的采样值，ik(k=1～N)为N次原始采样值队列，imax和imin分别为ik队列的最大值和最小值。当获取一个新原始采样值后，该值入队，原队列的首个数据出队，依次类推。

图6所示为软件滤波前后，输入电流值分别为4mA、12mA、20mA时，1 000次采样数据的分布对比图，图中同时标示出了采集数据的标准差，可以看出，经过软件滤波后，采样数据的标准差大大减小，分布更加集中。但是，采样电流值与输入电流值相比，仍有恒定的正偏置误差。不同通道的最大采样误差随输入电流的关系如图 7所示。

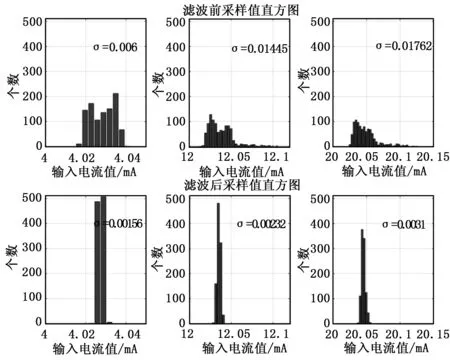
图6 滤波前后，1 000次采样数据的分布直方图对比

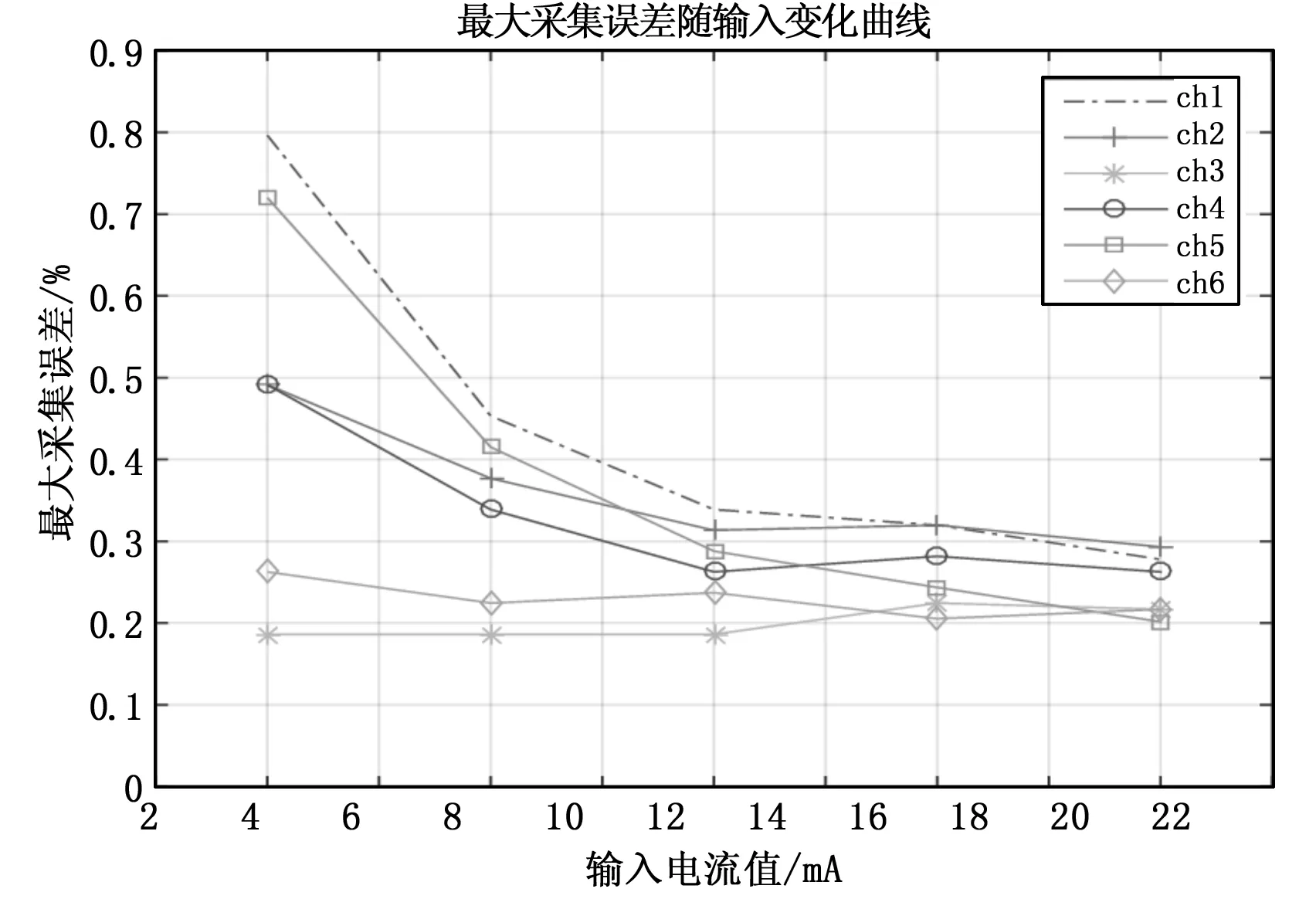
图7 六通道模拟信号最大误差随输入电流变化曲线

2.3 最小二乘估计

SAD3578的输入引脚输入-10～+10V的模拟信号，通过图 8[3]所示的电路转换为0～4V的模拟电压，再与4V的参考电压相比，得出最后的转换值。

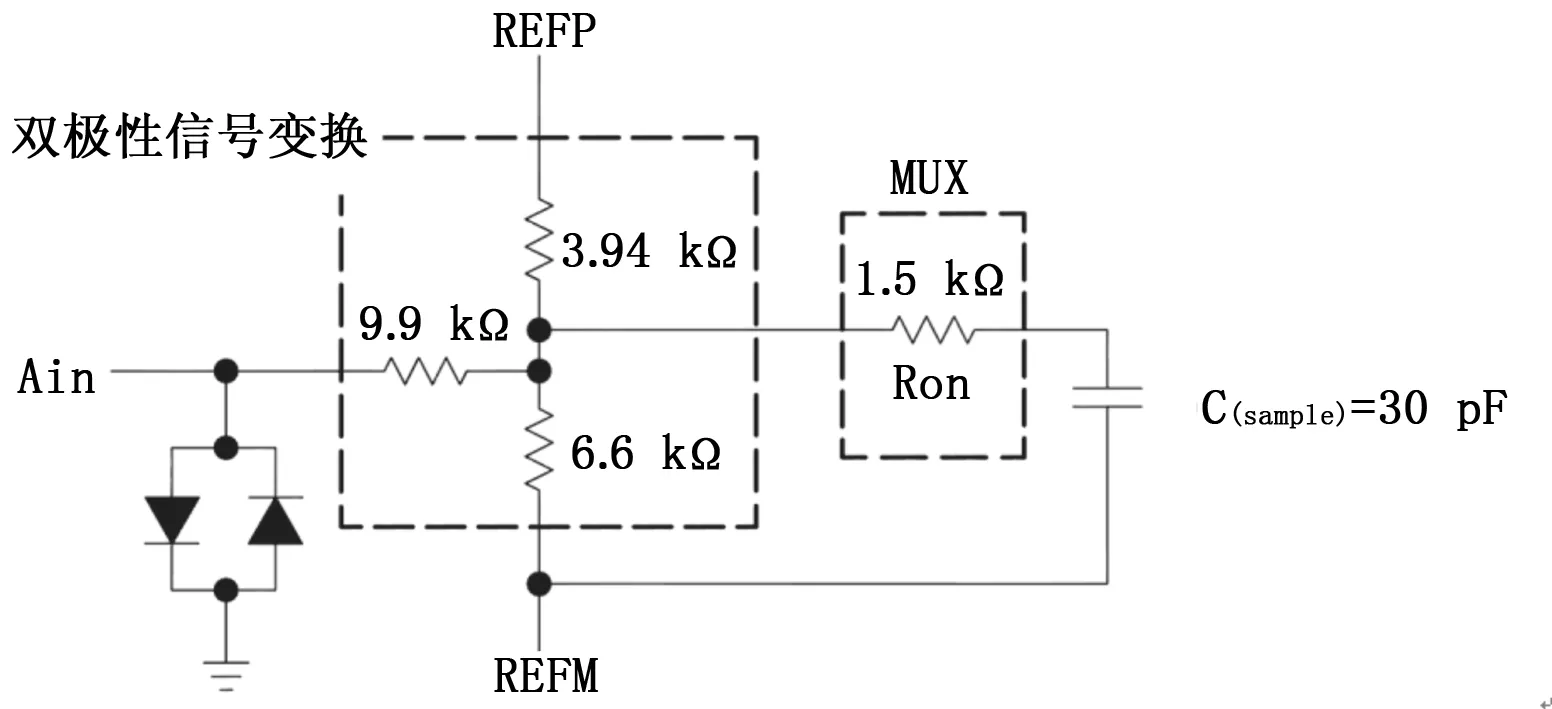
图8 SAD3578内部模拟输入端电压转换电路

根据基尔霍夫电流定律，信号Ain经过图 8所示的电路后，输出电压Vo与Ain的关系如公式6所示，当Ain范围为-10～+10 V时，Vo输出范围为0～4 V。由于工艺问题，图 8中的电阻存在误差，使Vo和Ain的关系并不严格成公式6所示的比例关系，而且各通道之间的一致性也不好，使得采集结果存在增益误差和偏置误差，造成了采集误差偏大，超出了指标要求。

(6)

由于阻性元件为线性元件，ADC的输入输出之间的关系为线性关系，因此，通过采集多个已知电流值的数据，利用最小二乘和一元线性回归方法对数据进行处理，拟合出一条最佳直线[4]，如公式(7)所示。

(7)

其中:is为采样获得的电流值，ii为输入的实际电流值。a、b的最佳估计值由公式(8)[5]得出。

(8)

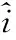
(9)

由于不同的芯片之间，同一芯片的不同通道之间，一致性不好，造成每个通道的拟合参数都不一样。因此，不能采用给某个通道输入不同的固定电流值，通过对采样结果进行拟合，对其它通道进行校正的在线校正方法。只能在产品出厂调试时对ADC的各个采集通道分别进行软件修正，将拟合的两个参数存入电路中的铁电存储器或者其它非易失性存储器中。电路每次上电后，从存储器中读取参数，并加载到相应的程序中，即可实现高精度的模拟信号采集。

3 试验结果与分析

图 9所示为利用最小二乘估计进行软件校正前后，输入电流值分别为4mA、12mA、20mA时，1 000次采样数据的分布对比图，图中同时标示出了采集数据的平均值，可以看出，经过软件校正后，采样数据的平均误差大大减小。

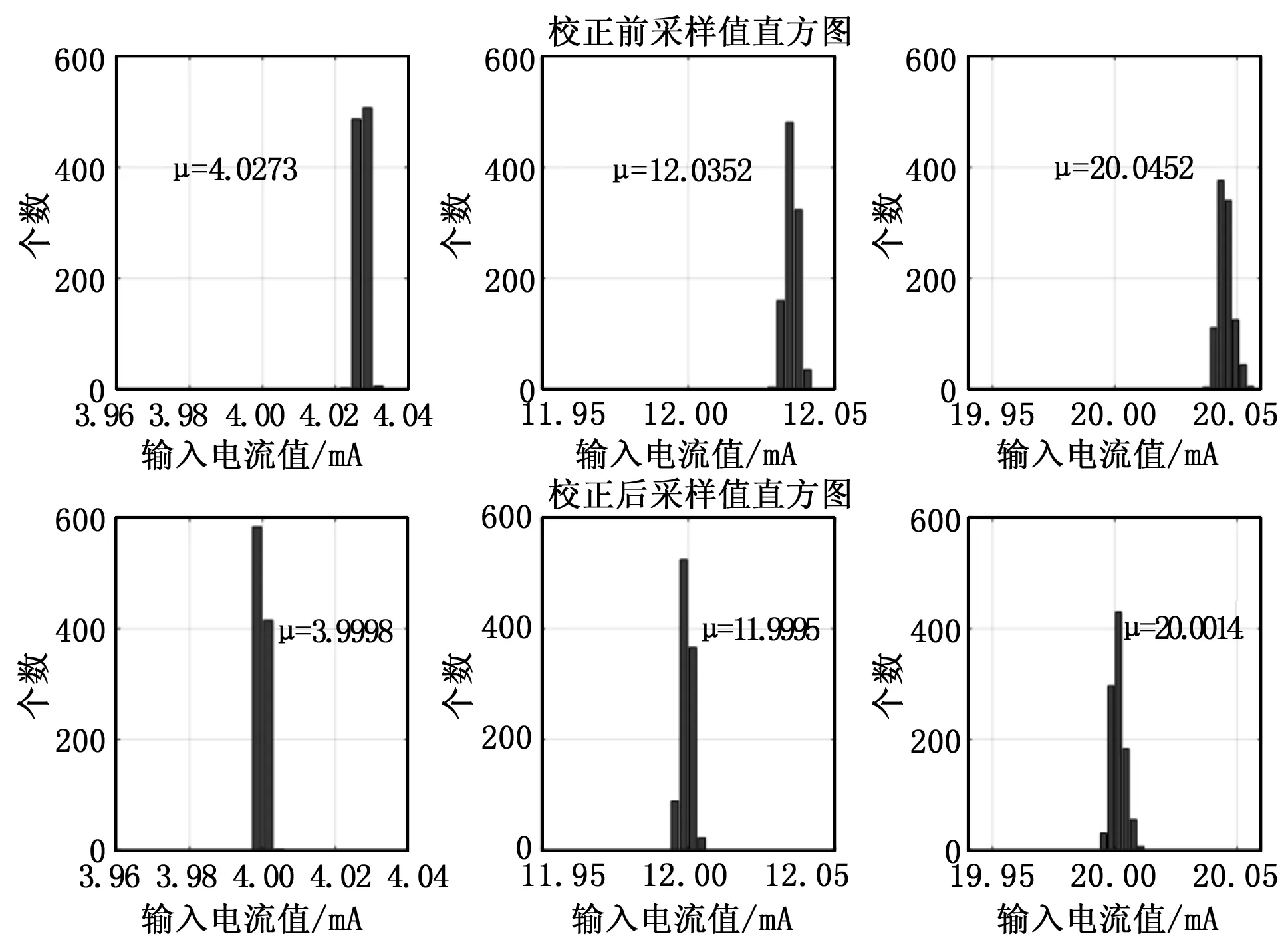
图9 校正前后，1 000次采样数据的分布直方图对比

图10所示为按照公式(9)，不同的通道在不同的输入电流下，校正前后的最大采集误差对比，可以看出，经过软件修正，输入信号在4～20mA的范围内时，采集精度大大提高，最大采样误差由0.8%提高到0.12%左右。

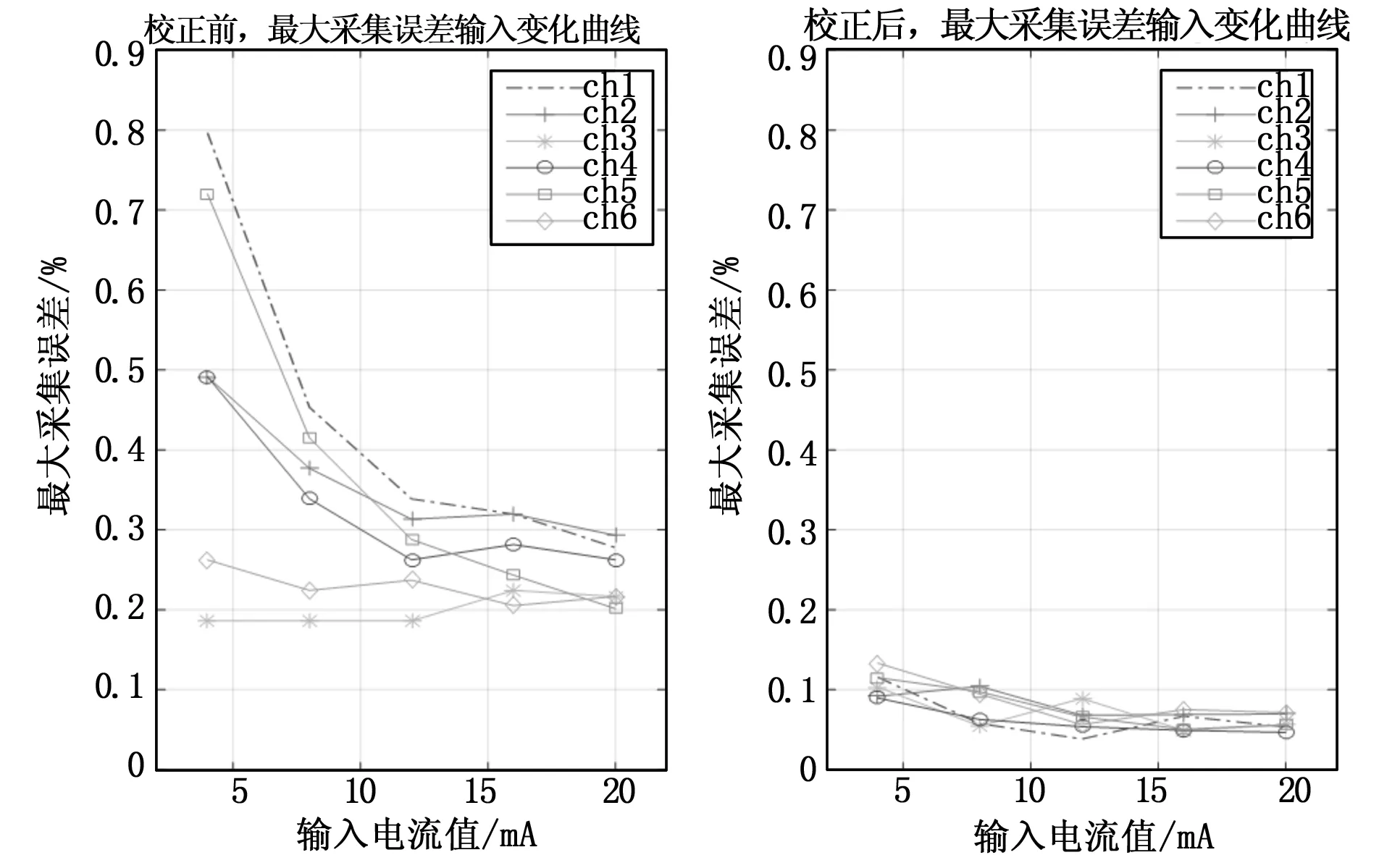
图10 校正前后，最大采集误差随输入电流变化曲线对比

4 结论

本文以国产的处理器和ADC芯片为核心，设计了一种模拟信号采集模块，并采用递推平均滤波方法和最小二乘估计方法，降低随机误差、固有偏置和增益误差，提高模拟信号的采集精度，使采样精度从校正前的0.8%提高到了0.12‰。试验结果表明，本文设计的模拟信号采集模块采样精度高，达到了同类型进口芯片的精度水平。

本文中的模拟信号采集模块全部采用国产化元器件进行设计，国产化率达到100%，并且元器件的质量等级均为普军级及以上，可靠性高，在有自主可控要求的装备中有良好的应用前景。

[1] 韩继国, 数据转换器走向国产化还有多远[J].集成电路应用, 2014(4).

[2] 中电24所.SAD3578数据手册[Z].2009.

[3]TI.TLC3578数据手册[Z]. 2003.

[4] 何 平, 王继坤, 岳长进.一种提高DSP的ADC精度的方法[J].科学计算与信息处理,

[5] 何书元.概率论与数理统计[M]. 北京:高等教育出版社, 2006.

A Method for Improving Sample Accuracy of Domestic ADC Module

Zhou Yongming1, Xu Jinliang1, Wang Shuwei2, Wang Zhenzhen1, Zhang Hongbin1

(1.Beijing Institute of Space Launch Technology, Beijing 100076,China;2.Beijing Institute of Aerospace Systems Engineering, Beijing 100076,China)

To solve the problem of equipment’ independence, a completely domestic multi-channel analog signal acquisition circuit based on domestic CPU and ADC was designed. Because of the low precision of the current domestic analog chip, especially the analog-to-digital converter chip, the precision of the analog signal acquisition module was low, making the practicability poor. In order to improve the sample precision, the recursive average filtering method was used to suppress the periodic interference and reduce the random error. Secondly, a linear regression was performed on the pre-measured values, and the sample values were estimated by the least squares method to reduce the inherent offset error and gain error. It could be concluded from the experiment results that the acquisition circuit could acquire multi-channel analog signal simultaneously, and had high acquisition precision. The biggest sample error was reduced from 0.8% to 0.12%. There was good consistency between the module’s channels. The module was of high reliability and of 100% domestic rate, making it have good prospect for application.

improve; domestic ADC; sample accuracy; recursive average filter; least square estimation

2016-08-30；

2016-09-22。

周永明(1988-)，男，山东潍坊人，硕士研究生，工程师，主要从事应用电子技术方向的研究。

1671-4598(2017)02-0149-04

10.16526/j.cnki.11-4762/tp.2017.02.041

TH86

A