基于改进sigmoid激活函数的深度神经网络训练算法研究

黄 毅, 段修生, 孙世宇,郎 巍

(1.军械工程学院 电子与光学工程系,石家庄 050003;2.77156部队,四川 乐山 614000)

基于改进sigmoid激活函数的深度神经网络训练算法研究

黄 毅1, 段修生1, 孙世宇1,郎 巍2

(1.军械工程学院 电子与光学工程系,石家庄 050003;2.77156部队,四川 乐山 614000)

针对深度神经网络训练过程中残差随着其传播深度越来越小而使底层网络无法得到有效训练的问题,通过分析传统sigmoid激活函数应用于深度神经网络的局限性，提出双参数sigmoid激活函数;个参数保证激活函数的输入集中坐标原点两侧，避免了激活函数进入饱和区，一个参数抑制残差衰减的速度，双参数结合有效地增强了深度神经网络的训练;用DBN对MNIST数据集进行数字分类实验，实验表明双参数 sigmoid激活函数能够直接应用于无预训练深度神经网络，而且提高了sigmoid激活函数在有预训练深度神经网络中的训练效果。

深度神经网络；残差衰减；sigmoid激活函数

0 引言

深度神经网络自被提出以来，已被广泛应用于图像识别、语音识别、自然语义理解等领域。但是，与浅层神经网络(包含1个隐层)相比，深度神经网络的训练要难得多，其主要原因是梯度下降算法中残差会随着传播深度越来越小，使得底层网络由于残差过小而无法得到有效的训练。目前，解决该问题方法主要有两种：一是采用预训练算法等更好的权阵初始化方法；二是更好地激活函数。

本文通过分析传统sigmoid激活函数在深度神经网络训练中的局限性，提出双参数sigmoid激活函数，提高sigmoid激活函数应用于深度神经网络的性能。

1 sigmoid激活函数的局限性

sigmoid函数是深度神经网络中应用最为广泛的激活函数之一，其函数及其导函数为：

(1)

在sigmoid激活函数应用于深度神经网络训练时，制约深度神经网络训练效果的因素仍然是残差，但主要表现在两个方面；一个是激活函数的输入值大小对残差的影响；另一个是深度神经网络底层数对残差的影响。

激活函数的输入值过大过小，都会对深度神经网络的训练效果产生影响。假设激活函数的输入net=WTX，当net整体过小时，如图1(a)所示，输入net主要集中在原点左右，不同神经元激活值相近，导数值亦相近，此时激活函数近似为线性，无法对输入数据进行有效区分，神经网络无法训练。

图1 输入过大和过小的sigmoid导函数

当net整体过大时，如图1(b)所示，net主要集中在坐标轴两侧，激活值大量为0，由残差公式可知，此时经元残差趋近于0，权值矩阵的修正量也为0，神经元进入激活函数的饱和区，神经网络无法训练。因为激活函数输入过小时，适当增大权值就能解决解决，所以激活函数输入值对深度神经网络的影响主要集中表现在输入值偏大问题上。

深度神经网络的层数对其训练效果同样有很大影响，一方面，层数越大，其学习得到的特征越紧密，表达能力越强，另一方面，层数增大，训练难度也越大。其主要原因是在经典的误差反向传播算法中(残差表达式如下)，由于sigmoid激活函数的导数值f′恒小于1，而残差在由输出层向底层反向传播过程中，每经过一个隐层，其残差值乘以f′，这样经过多层后，深度神经网络因底层残差太小而无法得到有效训练。

(2)

其中:δ(nl)为输出层残差，ο(nl)为输出层的实际输出，y为输出层的期望输出，δ(l)为隐层残差，net为激活函数f的输入。

2 双参数sigmoid激活函数

针对因激活函数输入过大导致的神经元进入饱和区的问题，引入第一个参数α(0<α<1)。通过压缩激活函数的输入，αnetl向坐标轴中心靠拢，导数值f′(αnetl)增大。改进后的激活函数公式和残差公式为：

(3)

引入参数α虽然解决了神经元饱和区的问题，但是使残差衰减α(nl-l-1)倍，加重了残差衰减。

针对残差衰减过快的问题，在激活函数的导函数中引入第二个参数λ(λ>1)，改进后的激活函数公式和残差公式变为：

(4)

其中:α，λ是两个相互独立的参数。

激活函数导函数f′增大λ倍，深度神经网络第l层残差增大λ(nl-l-1)α(nl-l-1)倍。通过调整选取合适的α和λ，一方面可以修正由于网络层数过大导致底层过小的残差，另一方面可以解决引入α参数加重残差衰减的问题。

(5)

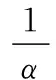
图2 双参数sigmoid激活函数BP算法流程图

双参数sigmoid激活函数的BP算法推导如下：

第一步：输入样本(xi,yi)，i=1,…,m，计算各层输出：

(6)

第二步：计算输出误差:

(7)

第三步：计算各层误差信号:

(8)

第四步：调整各层权值:

(9)

其算法流程如图3所示。

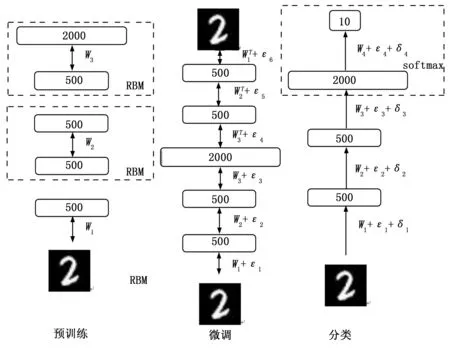
图3 DBN训练过程

3 基于MNIST数据集的DBN实验

深度信念网络(DBN)是一种典型的深度神经网络，本节将通过DBN实验的方式验证双参数sigmoid激活函数的有效性。采用MNIST数据集为实验数据，MNIST数据集是美国中学生手写阿拉伯数字数据集，共有60 000个28*28维的0～9的阿拉伯数字的手写样本，取50 000个样本作为训练数据，10 000个样本作为测试数据进行数字分类实验。

设计一个深度信念网络(DBN)，其网络结构为784-500-500-2000-10。 运用贪心逐层算法对深度神经网络进行预训练，其训练过程为：将MNIST图片数据转化为784维的向量数据，经过归一化和白化预处理，输入到DBN中进行基于受限玻尔兹曼机(RBM)的无监督预训练，经过50次循环，得到特征矩阵W；将学习到的特征矩阵W传给相应的神经网络784-500-500-2000-500-500-784进行有监督微调，得到特征矩阵W+ε。之后将W+ε传递给神经网络784-500-500-2000-10，在不同sigmoid激活函数条件下，进行数字分类实验，训练周期数为300次，每隔10次采集一次测试误差数据，其训练过程如图3所示。

设置α=0.3,λ=3.3，在有预训练和无预训练两种情况下对双参数sigmoid激活函数和普通sigmoid激活函数进行数字分类实验，其测试结果如表1所示。

表1 测试误差 %

测试误差曲线如图4所示。其中，‘*’线表示普通sigmoid激活函数测试误差曲线，‘o’线表示双参数sigmoid激活函数的测试误差曲线；图4(a)是无预训练时测试误差曲线，图4(b)是有预训练时测试误差曲线。

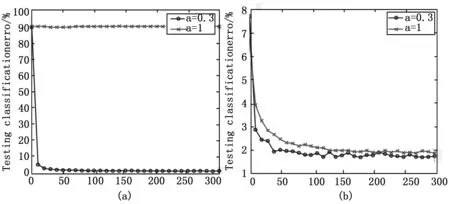
图4 测试误差与训练周期

分析图4可知：

1)双参数sigmoid激活函数可以直接应用于深度神经网络的训练而无需预训练。如图4(a)，传统的sigmoid激活函数的测试误差高达90.2%，无法对深度神经网络进行有效训练，双参数sigmoid激活函数训练效果明显，测试误差达到1.59%；

2)双参数sigmoid激活函数有比传统sigmoid激活函数更好的训练结果。如图4(b)，传统sigmoid激活函数的测试误差达到1.85%，双参数sigmoid激活函数的测试误差达到1.68%，综合1)的结论，有无预训练，双参数sigmoid激活函数均能取得比传统sigmoid激活函数更好的结果；

3)双参数sigmoid激活函数有比传统sigmoid激活函数更快的训练速度。如图4(b)，双参数sigmoid激活函数50次迭代就能达到1.92%的测试误差，而传统sigmoid激活函数要达到同样的测试误差则需要180次迭代。

为了研究双参数sigmoid激活函数对深度神经网络底层残差的影响，以深度神经网络底层的权阵调整量ΔW1的绝对值之和D作为观测量，用于表征底层残差的大小。

D=∑∑|ΔW1|

实验中，每隔10个周期，记录一次ΔW1，并求D，D随迭代次数的变化曲线如图5。其中，‘*’线表示普通sigmoid激活函数测试误差曲线，‘o’线表示双参数sigmoid激活函数的测试误差曲线；图5(a)为有预训练时D的变化曲线，图5(b)为无预训练的D的变化曲线。

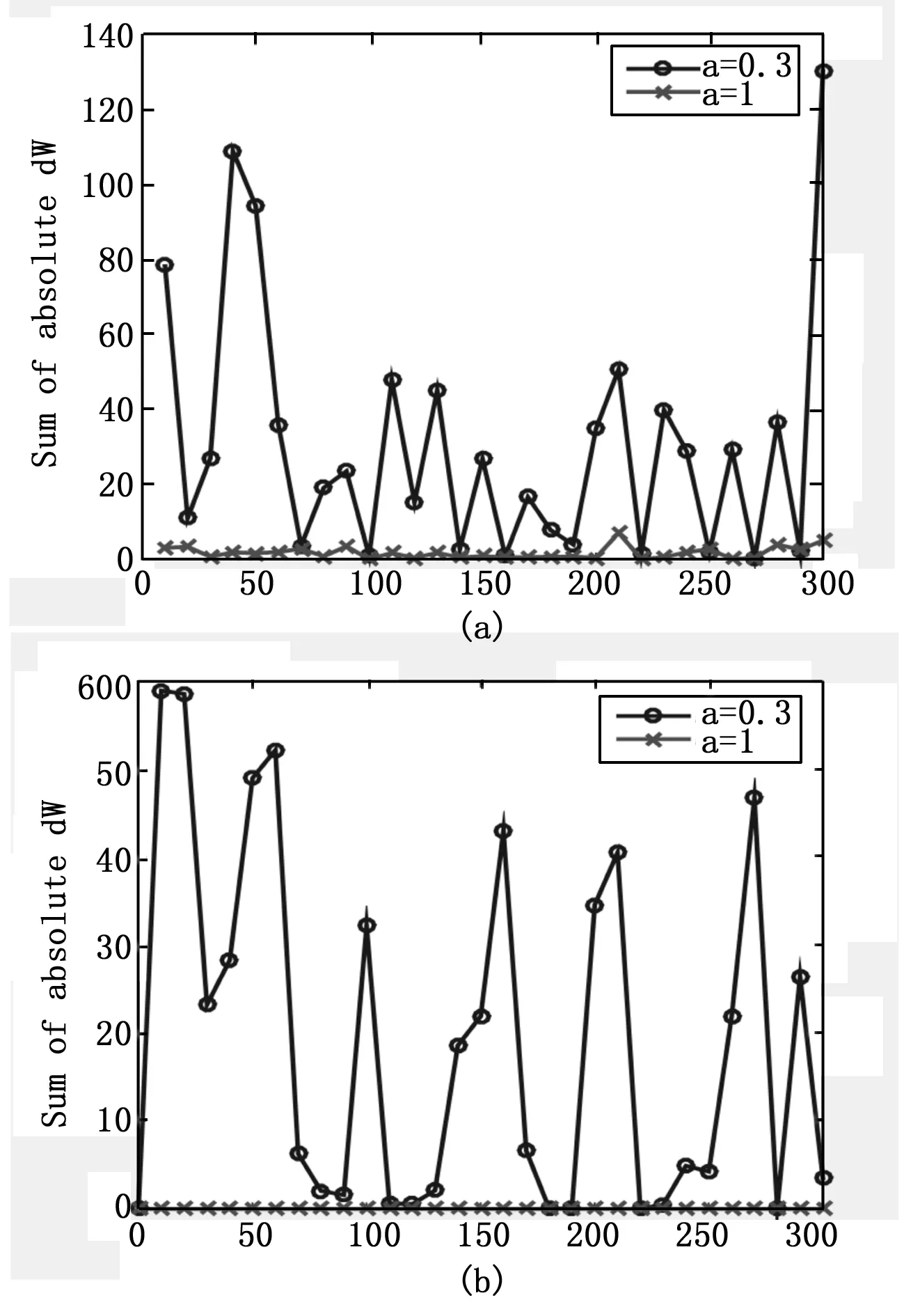
图5 D与训练周期

分析图5可知：

1)无预训练时，传统sigmoid激活函数深度神经网络不能有效训练的原因是其残差过小。如图5所示，无预训练时应用传统sigmoid激活函训练的深度神经网络的D的范围在10-10～10-8之间，而应用双参数sigmoid激活函数的深度神经网络中D的范围在0.017 9～58.936 6之间，即无预训练时，较之传统sigmoid激活函数，双参数sigmoid激活函数将残差增大了将近107倍，这是无预训时练深度神经网络能够有效训练的关键；

2)与传统sigmoid激活函数相比，双参数sigmoid激活函数有更大的残差，这是双参数sigmoid激活函数有更好训练效果的原因所在。如图5(b)，有预训练时，应用双参数sigmoid激活函数训练的深度神经网络的残差仍然比应用传统sigmoid激活函数的残差大，综合1)的结论，即有无预训练，应用双参数sigmoid激活函数的深度神经网络的残差都比应用传统sigmoid激活函数的大，这是其取得较好训练效果的原因所在。

4 结论

本文针对深度神经网络深度训练过程中底层残差过小的问题，从分析sigmoid激活函数的局限性出发，提出双参数sigmoid激活函数，有效的增大了底层残差，提高了深度神经网络的训练效果，结合深度信念网络(DBN)对MNIST数据集进行分类实验，实验结果显示：

1)有无预训练，较之传统sigmoid激活函数，应用双参数sigmoid激活函数训练的深度神经网络均可取得更好的训练效果；

2)有无预训练，较之传统sigmoid激活函数，应用双参数sigmoid激活函数训练的深度神经网络均可获得更大的底层残差，这是取得较好训练效果的关键因素。

[1] Sun Y, Wang X, Tang X. Deep Learning Face Representation from Predicting 10000 Classes[A]. Proc. of the IEEE Conference on Computer Vision and Pattern Recognition[C]. Columbus, Ohio,2014.

[2] Taigman Y, Yang M, Ranzato M A, et al. Deepface: closing the gap to human-level performance in face verification[A]. Proc. of the IEEE Conference on Computer Vision and Pattern Recognition[C]. Columbus, Ohio,2014.

[3] Mohamed A, Dahl G E, Hiton G. Acoustic modeling using deep belief networks[J]. Audio, Speech, and Language Processing, 2012, 20(1):14-22.

[4] Shen Y L, He X D, Gao J F, et al. Learning semantic representations using convolutional neural networks for web search[A]. Proc. of the of the 23th International Conference on World Wide Web[C]. Seoul, Korea,2014.

[5] Jin-Cheng, Li Wing, W. Y. Ng Daniel, et al. Bi-firing deep neural networks[J]. Int. J. Mach. Learn. & Cyber, 2014(5):73-83.

[6] Ranzato M, Poultney C, Chopra S, et al. A sparse and locally shift invariant feature extractor applied to document images[A]. International Conference on Document Analysis and Recognition (ICDAR’07)[C]. Curitiba, Brazil,2007.

[7] Hinton GE, Osindero S, The Y. A Fast Learning Algorithm for Deep Belief Nets[J]. Neural Computation, 2006, (18):1527-1554.

[8] Bengio Y, Lamblin P, Popovici D, Larochelle H. Greedy Layer-wise Training of Deep Networks[J]. Neural Information Processing Systems, 2007:153-160.

[9] Erhan D, Bengio Y, Courville A, Manzagol PA, Vincent P, Bengio S. Why does Unsupervised Pre-training Help Deeplearning[J]. J. Mach. Learn. Res., 2009 (11):625-660.

A Study of Training Algorithm in Deep Neural Networks Based on Sigmoid Activation Function

Huang Yi1, Duan Xiusheng1, Sun Shiyu1, Lang Wei2

(1.Department of Electronic and Optical Engineering, Ordnance Engineering College, Shijiazhuang 050003, China;2.77156 Army, Leshan 614000, China)

Aiming at the problem that residual error gets smaller with the depth of propagation increasing and the bottom of DNN trains ineffective, by investigating the limitations of sigmoid activation function in DNN, a sigmoid activation function with two parameters is proposed. One parameter makes the input of sigmoid activation function concentrate in sides of the origin, and another parameter restrains the decreasing speed of residual error. The combination of two parameters enhances the training of DNN. Do number classification experiments on MNIST using deep belief networks(DBN), the results show that sigmoid activation function with two parameters can be used in DNN directly without pre-training and improve the performance in DNN with pre-training.

deep neural networks(DNN); gradient diffusion; sigmoid activation function

2016-08-12；

2016-09-16。

黄 毅(1992-)，男，湖北孝昌人，硕士生，主要从事深度神经网络和故障诊断方向的研究。

1671-4598(2017)02-0126-04

10.16526/j.cnki.11-4762/tp.2017.02.035

TP183

A