钢筋混凝土式风机基础抗扭刚度计算试验研究
2017-03-20汪睿,程宵,周凯
汪 睿,程 宵,周 凯
(1.水能资源利用关键技术湖南省重点实验室,湖南长沙410014;2.中国电建集团中南勘测设计研究院有限公司,湖南长沙410014)
0 引 言
近几年来,我国风力发电事业发展迅速,风力发电总装机容量显著增加,但机组的安全事故也时有发生,风机基础的刚度与其结构安全性具有直接联系。在当前的风电场设计中,风电机组生产厂商一般是基于一个假定的基础扭转刚度提出上部荷载,因此会对基础的抗扭刚度提出明确的要求。为确保风电机组基础设计的安全性和经济性,在风机基础的初步设计完成后,应核算其抗扭刚度。建筑结构的重量及承受的荷载是通过土的支承力和地下水浮力保持平衡,各自的工作性状(例如变形、内力、应力)不仅取决于荷载的大小和分布,在一定意义上更取决于上部结构、基础、地基三者抵抗变形的刚度大小及其相互关系[1]。
目前,有关复合地基抗扭刚度的计算公式难以全面反映诸多因素的综合作用。本文利用有限元数值模拟的方法,对风机基础进行抗扭刚度的计算,并根据GB50040—96《动力机器基础设计规范》对计算结果进行验证,结果表明有限元数值模拟的方法可靠、有效。
1 计算理论
本文以基础结构(包括承台、桩以及地基基础三个部分)的抗扭刚度作为主要研究对象,通过有限元计算得到基础结构对外荷载的抵抗能力。理论上,力学中的刚度计算基于两个理论基础,即线弹性和小变形假设。由于土是非线性结构,从理论上分析地基基础的刚度显然是随外加荷载变化而相应变化的,即复合地基基础的刚度并非一个恒定的数值。因此,本文所建模型做如下简化:
(1)将土体材料简化成线弹性模型。线弹性理论模型是目前主要用于描述混凝土应力和变形关系的本构模型之一,其特点在于服从广义胡克定律,即应力应变在加载时呈线性关系,卸载后材料无残余应变,用线弹性模型模拟应力水平较低的混凝土材料是基本符合实际的;并且,通过对比重力场和实际外加荷载引起的应力水平,前者远远大于后者。基于以上结论,本文认为在实际外载荷作用水平下,将土体简化为线弹性模型具有一定的精度且容易收敛,大幅度提升了计算分析的效率。
(2)采用Combin39单元模拟桩土之间的相互作用。Combin39单元可用于模拟物体间切向的粘结滑移,能近似模拟法向仅能受压而不能受拉的特性(相对更适用于弹簧和拉索),故采用Combin39单元模拟桩土之间的相互作用是合适的。
(3)完整的风电机组包括桩、风机基础、塔筒以及叶轮等多个组成部分,本文中桩和基础统称为下部结构,塔筒及以上的部分则统称为上部结构。本文重点考虑下部结构的刚度,即假定本基础上部结构的刚度为完全柔性,对基础的变形毫无约束作用,因此实际得到的扭转刚度是一个偏小值,其满足基本的设计理念和规范要求。
2 计算模型
根据以上理论基础建立相应的有限元模型,为便于计算和分析,对模型的属性和边界条件等都进行了相应简化。
2.1 单元类型
根据工程实践经验,利用实体单元模拟混凝土承台及土体可以得到较为完整的应力分布情况。由于桩在轴向的几何量级远大于其界面,采用梁单元模拟桩,既可以满足精度要求,又能达到简化几何模型、提高计算效率的目的。
2.2 材料参数
对于混凝土承台,虽然其中有钢筋,但配筋率较小,所以将其取为素混凝土的材料参数,同时这样处理的计算偏于安全。
对于桩,参考设计图集中的截面性质及钢筋布置情况,根据钢筋与混凝土体量比计算出等效弹性模量。另外考虑到桩中的钢筋与混凝土的粘结情况很好,可认为钢筋与混凝土是协同变形,故泊松比取二者中较小值,即混凝土的泊松比。
对于地基土,剪切波速vs与剪切模量G之间的关系为
(1)
式中,ρ为土体密度。弹性模量E与剪切模量G的关系为
(2)
式中,υ为泊松比。故由式(1)、(2)可得
(3)
根据勘测给出的剪切波速vs=160 m/s,并取υ=0.25,由式(2)、(3)可求得土体弹性模量E=1.344×108Pa,剪切模量G=0.537 6×108Pa。模型材料参数见表1。
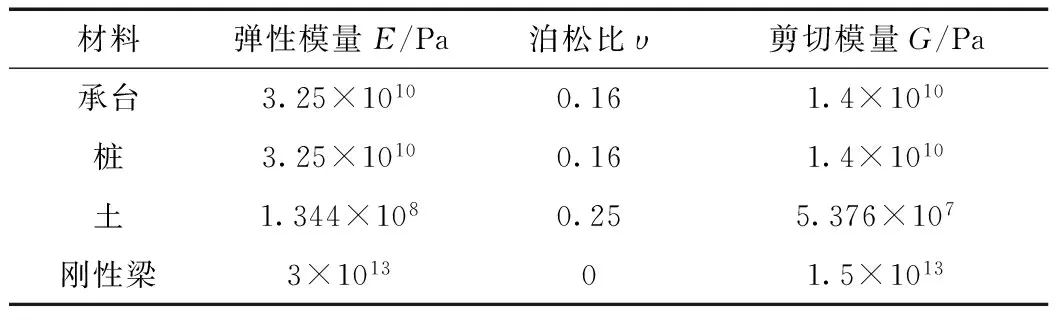
表1 模型材料参数
2.3 载荷施加方案
荷载施加点应在基础顶部法兰点,但根据有限元计算的特点,若直接在法兰点加载,会引起严重的应力集中。并且在施加弯矩的时候,容易产生局部效应,致使结构受力特性与实际不符。故考虑在法兰点处加上一个刚性短梁,此梁弹性模量取混凝土的100倍,以近似实现梁体相对刚性。同时,梁长取值需使最终的位移值收敛,以消除外加刚性梁对最终结果的影响。经过试算,梁长度取为0.1 m时可满足要求。另外,法兰点处需用约束方程实现刚性梁与承台的连接,并提取节点处六个自由度的位移,从而得到相应的刚度矩阵。结构有限元模型如图1所示。
3 有限元分析及其结果
外荷载与承台底面位移的关系为{F}=[K]{U}。对于坐标系统,水平方向为X和Y坐标,施加水平剪力和弯矩;竖直方向为Z坐标,施加轴向力和扭矩。
通过施加单位荷载,并通过矩阵变换,得到法兰盘处的节点刚度矩阵,即
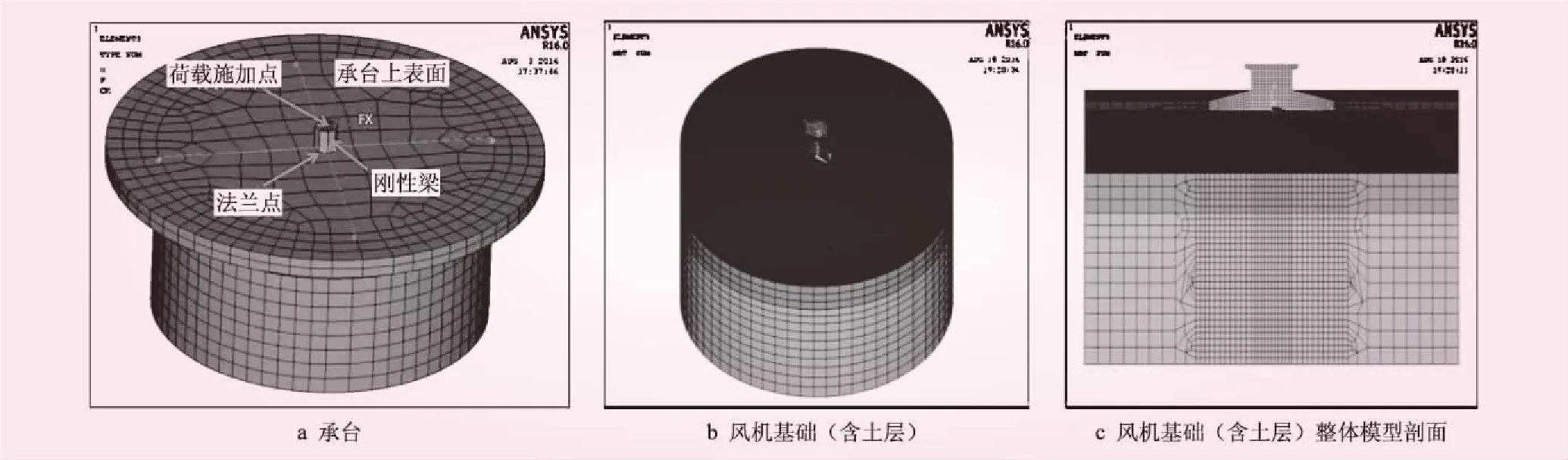
图1 构建的结构有限元模型示意

从刚度矩阵计算结果可以发现,基础整体结构在法兰盘点处扭转刚度为2.3478×1011N·m/rad。
根据GB50040—96《动力机器基础设计规范》[7],计算得到天然地基的抗扭刚度Kψ=2.359×1011,这与有限元分析得到的结果基本一致。
4 结 语
本文通过有限元分析的方式探索计算风机地基基础扭转刚度的方法,并采用规范推荐的公式进行了验证。计算结果表明,简化的有限元方法可靠、有效,但在一定程度上偏于保守,若要得到风力发电机组整机刚度的相对精确解,还应建立桩的实体模型,考虑桩与土之间接触的相互作用及土的非线性本构模型,并建立完整的上部结构(含塔筒、法兰、叶轮、轮毂及其他内附件等效质点)模型。
[1] 孙帅, 逯芳. 刚度理论在地基基础设计中的应用[J]. 建筑科技与管理, 2010, 48(6): 61- 62.
[2] 张应之, 刘茂盛, 李晔东. 对天然地基抗压刚度系数CZ的讨论[J]. 工业建筑, 2014, 44(6): 10- 13.
[3] 潘复兰. 地基抗压刚度系数随深度变化的分析[J]. 固体力学学报, 1981, 2(1): 54- 63.
[4] 李席珍. 天然地基抗压刚度系数的几种确定方法[J]. 工程勘察, 1984, 12(1): 73- 77.
[5] 涂正武. 任意地基中桩的刚度计算[J]. 建筑科学, 1992, 8(1): 21- 35.
[6] 郭福盛, 张绍银. 框架结构与地基协同作用的计算分析[A]∥辽宁岩石工程技术[C]. 沈阳: 辽宁省土木建筑学会, 2001: 168- 171.
[7] GB 50040—96 动力机器基础设计规范[S].
