寒区引水隧洞低温相变温度场-渗流场耦合模型及其数值模拟研究

姜海波,貊祖国,后雄斌,金 瑾

(石河子大学水利建筑工程学院,新疆石河子832000)

0 引 言

寒区隧洞围岩冻胀问题涉及到岩体的应力场、温度场、渗流场等多场耦合作用。国内外众多学者都致力于低温岩体“温度场—渗流场”耦合问题的研究[1-5]。基于连续介质或等效连续介质模型的裂隙岩体渗流场与温度场耦合作用是目前该领域研究的热点。岩体冻胀产生的根本原因是液态水在低温下相变成固态冰,相变过程中水的体积膨胀引起的冻胀力造成了岩体的冻胀破坏。大量工程研究表明：岩体中的裂隙水低温冻结膨胀会造成岩体的冻胀破坏,而冻结过程中水分不断向冻结锋面迁移、聚集并结晶成冰透镜体也是岩体产生冻胀的重要原因[6- 8]。TAKEDA等[9-12]对水热迁移机理及其相关问题进行了比较系统的分析和研究,还有学者提出了多个水、热耦合计算模型[13-15],并对模型的有效性进行了验证。然而,寒区岩体的冻胀是一个复杂的热力耦合和水冰相变过程,岩体的冻胀特性及冻融劣化机理涉及低温冻融环境下复杂的温度场(T)、渗流场(H)和应力场(M)的耦合问题。裂隙岩体中的水分迁移机制、冻胀力的计算及其萌生消散机制、裂隙冻融开裂扩展机制和岩体多次冻融强度损伤及稳定性评价等都是研究冻岩过程中亟待解决的关键问题。在T—H—M三场耦合作用下岩体的冻胀特性和冻融劣化规律方面,前人取得了一系列研究成果[1,16-17],但总的来说,国内外关于低温冻融循环作用下岩体的多场(温度场、应力场、渗流场及化学场等)耦合研究较多,并取得了丰富的研究成果。而关于低温相变条件下岩体温度场—渗流场耦合问题的研究并不系统,并没有考虑冻胀力的消散和低温冻融循环对围岩力学特性及其衬砌结构稳定性的影响。

鉴于此,本文基于连续介质力学、热力学、渗流力学,考虑低温相变对岩体温度场和渗流场的影响,结合低温冻结条件下围岩的温度场—渗流场耦合模型,采用有限元法对新疆某电站引水隧洞工程进行围岩的冻结过程分析,研究低温相变条件下隧洞围岩温度场和渗流特性的变化规律,对引水隧洞经受长时间持续冻结作用后的围岩温度场、渗流特征进行分析,定量分析长期低温冻结作用对隧洞围岩温度场及其渗透特性的影响,为引水隧洞的安全运行提供理论依据。

1 低温岩体温度场和渗流场耦合数学模型

低温冻结岩体是岩体骨架、孔隙水、冰以及空气组成的多相介质。在冻结的过程中,岩体中的空气对岩体相变的影响比较小,可以不考虑空气影响,因此可以假定岩体处于饱和状态。岩体的冻胀破坏是低温情况下水冰相变引起的,岩体温度的变化引起了水冰相变和水分迁移的发生。在低温相变过程中,热量的迁移受到了温度梯度和岩体孔隙对流换热的影响。低温条件下岩体的水冰相变过程受到水力梯度和温度梯度的作用,它们共同造成了水分不断地向冻结锋面迁移、聚集,最终加速了岩体的冻胀破坏。

根据以上分析,以及孔隙介质的对流换热原理,低温相变岩体介质热传导的微分控制方程为

(1)

低温岩体的渗透方程为

(2)

式中,S为比贮水系数,取常数；p为渗透压力；k为渗透率；η为水的粘滞系数,计算中取0.001 kg/(m·s)；Hg为重力水头；SP0为分凝势,在计算中温度低于冰点时为正常数,在高于水的冰点温度时取0；T为温度；QH渗流场的源或者汇。求解上述微分控制方程,在移动边界上必须满足连续性条件和能量守恒条件[18]。

对于低温岩体温度场与渗流场耦合问题,求解时需要知道的边界条件主要有两种,一种为Dirichlet边界条件(也称固定边界)[19]；另一种为Neumann边界条件(也称流量边界)[20]。在有限元计算时,采用这两类边界条件进行计算。

(1) 温度场边界条件和初始条件。Dirichlet温度边界为T=Ta,该边界条件可通过现场监测获得计算边界的温度值,一般认为在足够远处该温度值为一恒定的常数。Neumann渗流边界为-K该边界的取值,随温度梯度的变化而变化,在计算中,需要根据现场监测资料进行计算。

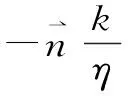
利用给定的边界条件,便可求解低温岩体温度场和渗流场。由于岩体在低温下其物理力学性质随温度变化而变化,且冻结缘带的位置也是不断变化的。因此,该问题为强非线性问题,不可能用解析方法求得其精确解,只有通过数值方法获得近似解。本文采用有限元方法对该问题进行数值分析,以获得较为精确的近似解。

2 寒区输水隧洞温度场与渗流场耦合有限元分析

2.1 工程概况

新疆某电站引水隧洞工程,地质情况较为复杂。一年冻结期达200 d,冰冻层平均厚度3～5 m,最厚达8 m。最冷月(1月)平均气温为-9.6 ℃,最热月(7月)平均气温为9.0 ℃,极端最低气温-37.6 ℃。考虑到该地区典型的大温差环境和长时间的冻结环境,施工及其隧洞运行的影响,原有的岩体温度场和渗流条件遭到破坏,可能出现的冻胀问题会影响隧洞的安全运行,因此需要对隧洞围岩的温度场和渗流场进行重点研究。结合当地历史气温及其现场监测资料,选用-30 ℃～+20 ℃的温度循环进行寒冻风化作用的叠加模拟,对引水隧洞经受长时间持续的冻结作用后围岩的温度场、渗流特征进行分析,从而定量分析长期低温冻结作用对隧洞围岩温度场及其渗透特性的影响,为引水隧洞的安全运行提供理论依据。

2.2 有限元计算模型、材料参数及其边界初始条件

该引水隧洞长2.5 km,为圆形隧洞,直径5 m,平均埋深7.5 m。由于隧洞较长,可以近似视为平面问题进行分析。根据引水隧洞模型的对称性,本文选用模型的1/2作为有限元计算区域,如图1所示。考虑到有限元计算的收敛性,当温度在-30～+20 ℃之间变化时,围岩的渗透系数随温度连续性变化而变化。考虑到低温情况下围岩孔隙水的相变,孔隙水的热物理学参数通过现场试验可获得,具体如表1所示。

材料密度/kg·m-3比热/J·(kg·K)-1导热系数/W·(m·K)-1相变潜热/J·kg-1孔隙率/%围岩36509001.8—0.37水100041800.56333000—冰917.521002.23——

热力学边界条件：AB、CD为对称边界,在该边界上满足-K；AF为固定边界,TAF=-15 ℃；DE为渗流边界,在该边界上满足-K在计算中,认为岩体的初始温度场均匀分布,即满足T|t=0=3.5 ℃。

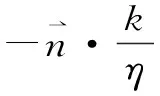
隧洞围岩的计算参数如表1所示。计算模型取时间步长为1 d,计算总时长取200 d。

2.3 计算结果分析

通过计算得到了不同时期隧洞围岩温度场的分布,如图2所示,图中“浅色”区域表示冻结区,“深色”区域代表为未冻结区。从图2可以看出,在给定的边界及其初始条件下,围岩在最初的10 d内,冻结速率非常快,隧洞断面冻深达到了21.25 m；在10～100 d,冻结深度呈现稳定增长的趋势,表现为冻结区范围扩大,未冻结区范围缩小；当计算时间为200 d时,温度场的分布趋于稳定。随着冻结时间持续,从计算结果中可以看出,冻结宽度随时间的推移不断增加。

分析图2可知,在最初的时刻,隧洞衬砌结构内的温度为-16 ℃,随着时间的持续,隧洞衬砌结构内的温度变化不大,在-16～-12 ℃之间变化。在计算区域内,受到岩体导热系数、相变潜热等因素的影响,随着水平深度的增大,冻结温度逐渐回升。冻结区与未冻结区的界面为冻结锋面,随着冻结时间的持续,冻结锋面向围岩内部推移。

含水岩体在冻结过程中,由于分凝势的作用,水分由未冻结区向冻结区迁移,如图3所示。根据有限元计算的结果,由于冻结温度的作用,孔隙中的原位水由未冻结区向冻结区迁移,渗流速度在冻结缘处达到最大,为1.359×10-4m/s,在未冻结区渗流速度较小,为4.1×10-6m/s。

3 结 论

(1)根据连续介质力学、热力学、渗流力学等理论,结合低温冻结条件下岩体的温度—渗流耦合模型,并考虑水冰相变和长期冻结作用对岩体温度场和渗流场的影响,分析了低温相变条件下隧洞围岩温度场和渗流特性的变化规律,定量分析了长期低温冻结作用对隧洞围岩温度场及其渗透特性的影响,模型可靠,计算结果具有一定的合理性。

(2)在长期的冻结过程中,围岩内部形成了冻结区与未冻结区；随着冻结时间的持续,冻结锋面向围岩内部推移。

(3)随着冻结时间持续,冻结宽度和深度随时间的推移不断增加,这将进一步加剧围岩的冻结范围和冻融损伤程度。需要说明的是,围岩冻胀问题涉及到岩体温度场、渗流场、应力场以及冻融损伤多场耦合作用,考虑低温相变的影响,围岩温度场和渗流特性对围岩冻胀损伤的影响还需更进一步的研究。

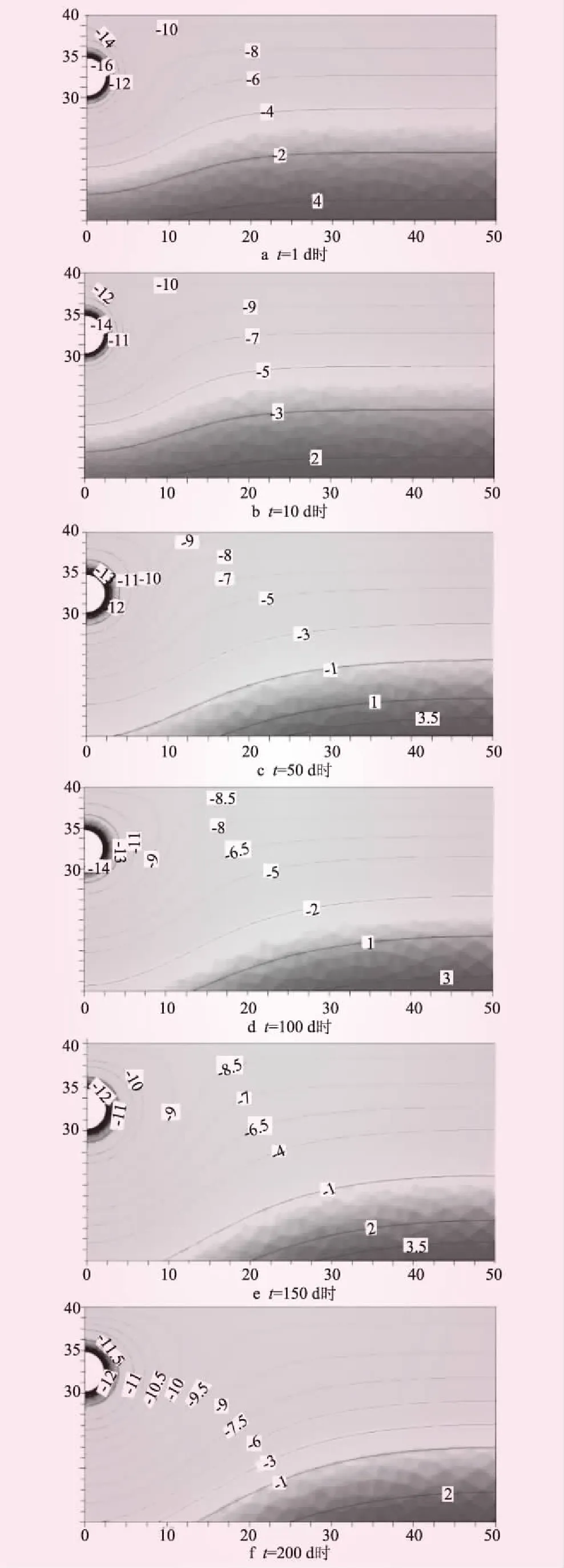
图2 隧洞温度场分布(单位：℃)

图3 200 d时渗流速度分布及其矢量方向

[1] NEAUPANE K M, YAMABE T, YOSHINAKA R. Simulation of a fully coupled thermo-hydro-mechanical system in freezing and thawing rock[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(5): 563- 580．

[2] 徐光苗, 刘泉声, 张秀丽. 冻结温度下岩体THM完全耦合的理论初步分析[J]. 岩石力学与工程学报, 2004, 23(21): 3709- 3713．

[3] KANG Y, LIU Q, HUANG S. A fully coupled thermo-hydro-mechanical model for rock mass under freezing/thawing condition[J]. Cold Regions Science and Technology, 2013, 95(11): 19- 26．

[4] 张国新, 沙莎. 混凝土坝全过程多场耦合仿真分析[J]. 水利水电技术, 2015, 46(6): 87- 93．

[5] AKAGAWA S, FUKUDA M. Frost heave mechanism in welded tuff[J]. Permafrost and Periglacial Processes, 1991, 2(4): 301-309．

[6] SETZER M J. Development of the micro-ice-lens model[C]∥International RILEM Workshop on Frost Resistance of Concrete. Bagneux: RILEM Publications SARL, 2002: 133- 145．

[7] MURTON J B, PETERSON R, OZOUF J C. Bedrock fracture by ice segregation in cold regions[J]. Science, 2006(314): 1127- 1129．

[8] OZAWA H. Thermodynamics of frost heaving: a thermodynamic proposition for dynamic phenomena[J]. Physical Review E, 1997, 56(3): 2811- 2816．

[9] TAKEDA K, OKAMURA A. Microstructure of freezing front in freezing soils[C]∥Proceedings of the 1997 International Symposium on Ground Freezing and Frost Action in Soils. Rotterdam: A A Balkema, 1997: 171- 178．

[10] KONRAD J M,DUQUENNOI C A. A model for water transport and ice lensing in freezing soil[J]. Water Resources Research, 1993, 29(9): 3109- 3124.

[11] LAI Y M, WU Z, ZHU Y, et al. Nonlinear analysis for the coupled problem of temperature and seepage fields in cold region tunnels[J]. Cold Regions Science and Technology, 1999, 29(1): 89- 96．

[12] HARLAN R L. Analysis of coupled heat-fluid transport in partially frozen soil[J]. Water Resources Research, 1973, 9(5): 1314- 1323．

[13] SHEPPARD M I, KAY B D, LOCH J P G. Development and testing of a computer model for heat and mass flow in freezing soils[C]∥The 3rd International Conference on Permafrost. Ottawa, Ontario: National Research Council of Canada, 1978: 76- 81．

[14] TAYLOR G S, LUTHIN J N. A model for coupled heat and moisture transfer during soil freezing[J]. Canadian Geotechnical Journal, 1978, 15(4): 548- 555.

[15] FUKUDA M. Experimental studies of coupled heat and moisture transfer in soils during freezing[R]. Institute of Low Temperature Science, Hokkaido University, Sapporo, Japan: 1982: 35- 91．

[16] NEAUPANE K M, YAMABE T. A fully coupled thermo-hydro-mechanical nonlinear model for a frozen medium[J]. Computers and Geotechnics, 2001, 28(8): 613- 637．

[17] LI N, CHEN B, CHEN F X. The coupled heat-moisture-mechanic model of the frozen soil[J]. Cold Regions Science and Technology, 2000, 31(3): 199- 205．

[18] 赖远明. 寒区隧道温度场、渗流场和应力场耦合问题的非线性分析[D]. 兰州： 中国科学院兰州冰川冻土研究所, 1999.

[19] KONRAD J M, MORGENSTERN N R. The segregation potential of a freezing soil[J]. Canadian Geotechnical Journal, 1981, 18(4): 482- 491．

[20] DRNEVICH V P, KONRAD J M. Procedure for determining the segregation potential of freezing soils[J]. Geotechnical Testing Journal, 1987, 10(2): 51- 58．