一种改进阈值函数与EMD结合的轴承故障诊断方法

陈焕亮，王立东



一种改进阈值函数与EMD结合的轴承故障诊断方法

陈焕亮，王立东

（辽宁科技大学电子与信息工程学院，辽宁 鞍山 114051）

在电机的振动信号中，若电机轴承发生故障，则故障通过一种周期性的循环冲击形式表现出来，而且通常伴随有噪声干扰在这里面，所以提取这个轴承的故障特征会变得困难。正文提出一种新的过滤噪声方法，该方法基于新的自适应阈值的改进阈值函数,可以滤掉小波分解细尺度上的噪声，并且细节系数此时也可以很大限度地保留下来，最终，噪声也在宽尺度上被高效地过滤掉。若将滤除噪声后的信号做 EMD处理，并且在选取IMF时，根据互相关系数结合峭度准则可以排除IMF分量在选择时候的无目的性。通过对仿真结果的分析，轴承故障能通过这种方法快速准确地检测出来，最终证明了这个方法的有效性。

电机故障；经验模态分解；小波分解；阈值

0 前言

在轴承力学特征中，作为一种重要的外在表现形式，我们可以通过振动信号观测结果来对轴承的故障情况进行诊断。虽然从故障的轴承得到的观测数据有大量的特征信息，但是仍然会包含大量的噪声。为使故障特征信息更高效地提取出来，会对观测数据进行滤除噪声。

在工程中，傅里叶变换法常用来去除噪声。但它不能对时间和频率进行定位，而且，在对非平稳信号进行分析的时候，也存在弊端。不过，当它进行小波变换时，能够在小波函数系拓展成的空间上被小波变换进行分解，最终得到在不同时间频率的投影。而且，其局部化特性[1]在时域和频域上同时都有较好的表现。小波软、硬两种阈值去噪法是Dohono[2]基于小波变换提出来的。因为噪声一般都是高频信号，所以小波分解的高频系数会被进行门限阈值处置，可以过滤掉噪声，适用于对时变信号的处理[3-5]。

本文提出一种新的去噪方法，立足于新的自适应阈值的改进阈值函数，对比目前纯粹基于最小均方差基础上方式，能更高效地提取出目标特征。在改进阈值函数基础上，同自适应阈值结合对小波系数进行量化纠正，是筛选出设备损坏信息特征的前提。

在1998年初，经验模态分解(EMD 即Empirical Mode Decomposition)法[6]被美籍华人N.E. Huang等人提出，因为有适用于解析非线性、非平稳信号序列的优势，文章将会提到用EMD，在降低噪声后收集轴承内圈的损坏信号，然后根据测定的数据来选取对应的IMF分量，最终获取到轴承内圈的故障信息。通过模拟实验获得的轴承运动信息，进一步的证实了该方法的有效性和准确性。

1 小波阈值理论

该理论的基本内容是：当轴承在运动时，信号在小波变换处理过后，大部分能量散布于少部分的系数中，而其它的则分布在少量的系数中，这表明了小波系数可以很好的承担局部能量[12]，同时在这些小波系数上，这些能量的分布都显示出一定规律。不过，进行小波变换后的噪声信号的系数，会在整个小波域内都有分布，其值会由变换时尺度的变大而缩小[12]。

假设未滤除噪声的信号的数学模型为：

评估其参数：对标准信号以及含有噪声的信号进行对比，采用均方误差的方法进行计算，最后值小的效果好。

2 改进阈值函数

过去使用小波阈值降噪时，会选择软、硬两种阈值函数，不能避免固定偏差和不连续性等缺陷[10]。

据此半软阈值函数的定义[8]，表达式如下：

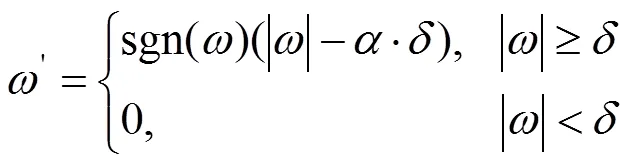
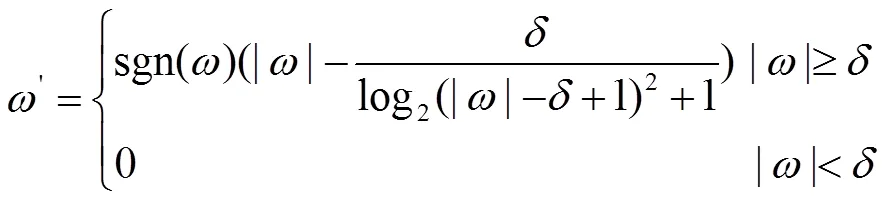
该函数在阈值点处，解决了原算法不具备连续性的问题，而硬阈值函数中的振动问题也可以规避，软阈值函数发生的误差有效地避免了[10]。不过它还是属于软阈值函数，针对软阈值函数这个特性，我们将软、硬阈值两种函数构成一种新阈值函数[10]。

针对这个想法，根据文献[9]并结合文献[10]提出公式(4)新算法，将该算法用于处理轴承振动信号。

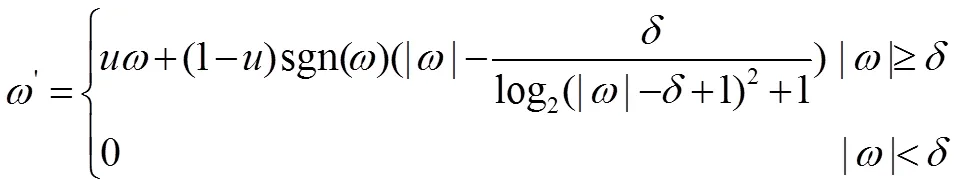
3 自适应阈值确定方法

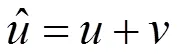
SURE是式(7)的一个无偏估计[11]，定义为：

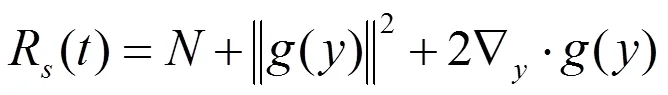
通过式(8)可得出：SURE与MSE对应的无偏估计和最小值存在关联关系，所以当上面的公式(8)结果达到最低值时，就是MSE条件下获得的最适阈值[12]。

4 EMD法

如何选择经EMD计算后的IMF分量，接下来引入两个准测，分别是互相关系数准则和峭度准则。

第一个准则：原始信号和假设的IMF条件之间的关系式：

第二个准则：是用于表示波形尖峰度的一个指标，其代表了峭度值，公式为：

5 算法验证

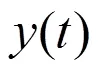
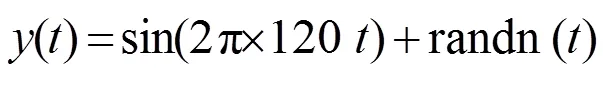
5.1 性能指标

原始信号与估计信号之间的均方根误差为：

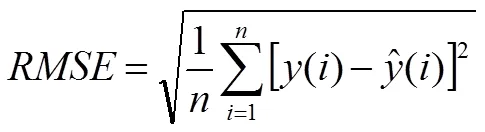
若越高，越小，实际信号和预计信号之间的差距就会缩小，证明了降噪的实效。

5.2 改进阈值函数降噪效果分析

表1给出了几种不同方式降噪的对比分析结果。从表中，改进与之函数所获得的值是最大的，而对应的值最小，因此，这种改进阈值函数的降噪效果也是最佳的。

表1 不同阈值函数降噪后信号SNR和RMSE对比

提高故障信号的识别能力，让信号能够及时反馈出来，使用EMD对滤噪后的估计信号进行新的解析，可以得到各个环节中的IMF。通过对前后信号采用两种准则进行运算分析，可以获得表2的相关系数和峭度值。

表2 各IMF与原始信号的互相关系数及各自峭度值

从表2的结果中，我们可以发现IMF序列2中两组数据的值是最大的，对IMF2做频谱分析获图1，由图1明显可得到特征频率120Hz的结论。

图1 IMF2频谱图

6 实例验证

实例引用的轴承滚动实验数据是USA Case Western Reserve University Department of Electrical Engineering and Computer Science测量得到，对其使用小波函数进行4层小波分解。设备以1750 r/min速度旋转，采样以12000Hz进行，收集到了4096个样点，轴承的型号为6205。通过公式可以计算出：

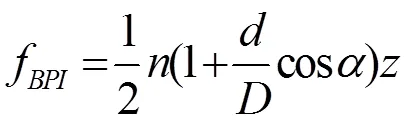
那么我们最终获得的轴承内圈故障频率为157.94Hz。对轴承故障的分析，应该抽取分层解析。我们首先抽取了四层的小波进行诊断，并得到了高频小波系数阈值，加以调整后进行计算，获得了信号如图2所示，通过和初始信号图进行对比分析，我们发现有些时域波形发生了变化。为了验证方法的可靠性，还要进行频域分析，进而判定故障是否真实存在。

我们采用EMD计算后的IMF值和残余值res，来获取故障特征率，如图3所示（取IMF1-4）。

计算出每个IMF值和降噪处理后信号的峭度值，并得到它们之间的关系系数，见表3。

图3 降噪后信号EMD分解（取IMF1-4）

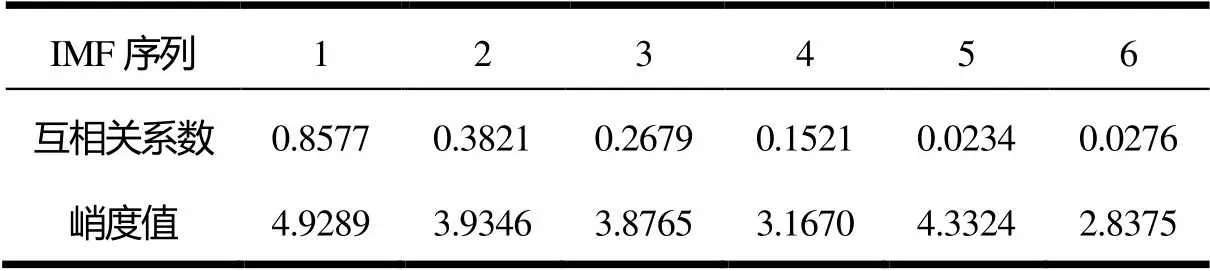
表3 各IMF与原始信号的互相关系数及各自峭度值

通过表3的数据，我们可以发现，IMF序列1符合准则的条件，通过对其进行包络谱分析，得到了图4。

图4 IMF1包络谱

从图4中，可以发现，当频谱在157.5Hz时，其能量波动范围较大，这和预计的故障数据高度吻合，进而可以判定轴承的内圈发生了故障。

7 结论

本文主要是通过改进阈值函数对采集的数据滤除噪声，并通过结合EMD分解提取轴承在故障时的特征信息，首先，我们将未经处理的故障信号使用小波阈值函数降噪来分解、重构，随之过滤噪声后的信号被EMD拆分成多个IMF值的和。最终，有着明显故障特征的IMF分量会被我们使用峭度—相关系数准则挑选出来，然后进行包络谱分析。而且在实验和仿真之后，得到的故障频率值与理论计算得到频率值相近，证实这个方式对轴承初期的故障信号有良好的降噪效果，故障频率也能被诊断出来，最终判定出故障种类。

[1] Giaouris D, Finch J W. Denoising using wavelets on electric drive applications[J]. Electric Power Systems Research, 2008, 78(4):559-565.

[2] Donoho D L, Martin V, Devore R L.et al. Data compression and harmonic analysis[J]. IEEE Trans. Inform. Theory, 1998, 44(6): 2435-2476.

[3] Donoho D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory,1995, 41(3):613-627.

[4] 秦前清, 杨宗凯. 实用小波分析[M]. 西安: 西安电子科技大学出版社，1994: 71-103.

[5] Grace Chang ,Yu Bin, Martin Vetterli. Adaptive Wavelet threshold-ing for Image Denoising and Compression[J]. IEEE Trans Image Processing, 2000, 9:1532-1546.

[6] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London Series A[J]. Mathematical and Physical Sciences, 1998: 903-995.

[7] Donoho D L, Johnstone I M. Wavelet Shrinkage: Asymp-topia[J]. Journal of the Royal Statistical Society, 1995, 57(2):301-369.

[8] 赵瑞珍, 宋国乡, 王红. 小波系数阈值估计的改进模型[J]. 西北工业大学学报, 2001, 19(4):139-142.

[9] 曹京京, 胡辽林, 赵瑞. 一种改进小波阈值函数的光纤光栅传感信号去噪方法[J]. 传感技术学报, 2015(4):521-525.

[10] 王立东, 张凯, 王良润. 改进小波阈值算法在电机振动信号降噪中的应用[J]. 电子技术应用, 2015, 41(5):77-80.

[11] Zhang X P, M.D. Desai. Adaptive denoising based on SURE risk[J]. IEEE Signal Processing Letters, 2002, 5(10):265-267.

[12] 吴光文, 王昌明, 包建东,等. 基于自适应阈值函数的小波阈值去噪方法[J]. 电子与信息学报, 2014, 36(6):1340-1347.

[13] 苏文胜, 王奉涛, 张志新,等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击, 2010, 29(3):18-21.

Improved Threshold Function Combined with EMD Method for Bearing Fault Diagnosis

CHEN Huanliang, WANG Lidong

(School of Electronic and Information Engineering University of Science and Technology Liaoning,Anshan 114051, China)

Bearing faults are always observed as cyclical impulses in the vibration signal, which mixed with noise and interference causing the difficulty of bearing fault feature extraction. A wavelet threshold function de-noising method based on an adaptive threshold is presented in this paper. By tuning parameters of threshold function, the noise wavelet coefficients are suppressed while the signal details are preserved as much as possible on the small scales of the wavelet transform, and on the other hand, the noise coefficients are removed to their maximum extent on the large scale. The signal denoising step is followed by empirical mode decomposition (EMD) in which, the selection of IMF follows cross-correlation and kurtosis criterion and the blindness of selection can be avoided. The results of analysis applied to simulated signal and the measured signal show that the bearing faults can be detected accurately.

motor fault; EMD; wavelet decomposing; threshold

TM307

A

1000-3983(2017)06-0047-05

2016-11-05

陈焕亮（1992-），硕士研究生，主要研究方向为信号处理、故障诊断。