基于非线性规划一维搜索的煤矿最优安全投资决策分析
2017-03-19刘晨宇
刘晨宇,刘 伟
(1. 重庆邮电大学 经济管理学院,重庆 400065;2. 华北科技学院 安全经济管理研究所,北京 东燕郊 065201)
一般情况,煤矿的安全投资和安全投入并不能用函数表示出来,特别是新建煤矿,这时传统理论用函数来表示煤矿的安全投资和安全投入,再用求极值、回归或边际等的办法求得煤矿的最优安全投资或安全投入的办法不能使用[1-13]。本论文根据非线性规划的基本概念和理论,运用非线性规划问题求解特点、直接一维搜索优化法和斐波那契法(Fibonacci)的基本思路[14,15],来求解煤矿的最优安全投资和安全投入,这样可以确保煤矿在若干年内就能寻找出本企业的最优安全投资和安全投入。
1 线性规划与非线性规划的最优解
1.1 线性规划的最优解的特点
线性规划的最优解的特点如图1(a)所示。设只有一个自变量x的线性规划问题,f(x)是线性函数,求Maxf(x),其中,x≤b,x≥a。从图1(a)显而易见,目标函数的最大值在点b上必可达到。反之,目标函数的最小值则可在点a上达到。点a和点b正是这个线性规划问题的可行解域的顶点。这个例子验证了线性规划的重要定理:线性规划问题如果有最优解,则一定可在可行解域的某一顶点上达到。
1.2 非线性规划的最优解的特点
非线性规划的最优解的特点如图1(b)所示。设只有一个自变量x的非线性规划问题,f(x)是非线性函数,求Maxf(x),其中,x≤b,x≥a。假设目标函数f(x)是只有一个自变量x的单峰函数,变量x的取值范围为[a,b]。点a和点b是这个非线性规划的可行解域的顶点,或称为约束区域的边界。与线性规划的最优解不同,此非线性规划的最优解x*并不在可行解域的顶点,而是在可行域以内。如果目标函数f(x)略有变化,则最优解x*将会在另一点上取得。由此得到一个重要的概念,非线性规划的最优解并不一定在约束区域的边界上达到,而根据不同的目标函数和不同的约束区域,其最优解可能在约束区域上(包括约束区域内的所有点和边界)的某一点上达到。
与线性规划相比,非线性规划最优解的情况要复杂得多。当非线性规划的目标函数和约束条件的变量较多、形式比较复杂时,求最优解是一项相当困难的工作。线性规划有单纯形法这一通用方法,而目前非线性规划还没有使用于各种问题的一般算法。非线性规划的解法种类很多,但各个方法都有本身特定的适应范围。
1.3 非线性规划的最优解问题
非线性规划最优解的求解方法可分为解析优化法和直接搜索优化法两类。其中,解析优化方法也可称为间接优化方法,其特点是首先建立描述研究对象变化规律的数学方程,再用数学解析的方法求出数学方程的最优解[2~13];而直接优化方法的优点是不需知道研究对象的严格的数学表达式,而在变量的取值上直接搜索,通过少数次试验,寻找其最优解。
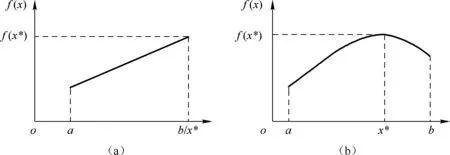
图1 线性规划与非线性规划最优解分析图
在实际工作中,建立研究对象的数学方程往往很困难,因而直接搜索方法的用途更广。其优点是:在不用增加设备、投资、人力和原材料的条件下,应用优选法可以缩短工时,增加产量,提高质量,节约原料,降低成本,挖掘潜力。目前应用最广泛的是配方配比、工艺操作条件、仪器仪表的调试以及工程最优设计等方面,但其在决定最优安全投资或安全投入方面的应用尚属空白。在企业安全投入方面,科学采用优选法是能够以较少试验次数迅速找到较优的安全投入方案。
1.4 企业安全投资具有非线性规划的特点
企业的安全投入分为安全投资(主动安全投入)和事故损失(被动安全投入)两部分,即安全投入=安全投资+事故损失。企业的安全投资(主动安全投入)可以事先计划确定,主要包括安全技术措施费、工业卫生措施费、安全教育费用、劳动保护费用和日常安全管理费用等;而事故损失(被动安全投入)具有一定的不确定性和风险性,主要包括:事故处理费、职业病诊治费、间接损失费和事故罚款等[10~13]。一般来说,企业的安全投资与事故损失之间往往存在一定的负相关关系,即安全投资越大,事故损失往往越小;安全投资越小,事故损失往往越大。因此,如以安全投资为自变量,安全投入为因变量,建立安全投资和安全投入的函数关系,当然大多数情况下,并不知道它们之间严格的数学函数表达式,即企业安全投入具有非线性规划的特点。上述思想用于安全投资决策,如对一个企业来说,很难求出安全投资或安全投入与企业经济效益的解析式,因此,求解企业安全投资的最优解使用直接搜索优化法更普遍。若已知企业安全投入的目标函数f(x)为下单峰函数(具体解析式未知),变量安全投资x的取值区间为[a,b]。求这个样一个非线性规划问题,可以采用一维搜索的方法。
2 斐波那契法的基本思路
2.1 一维搜索最优解解的基本理论
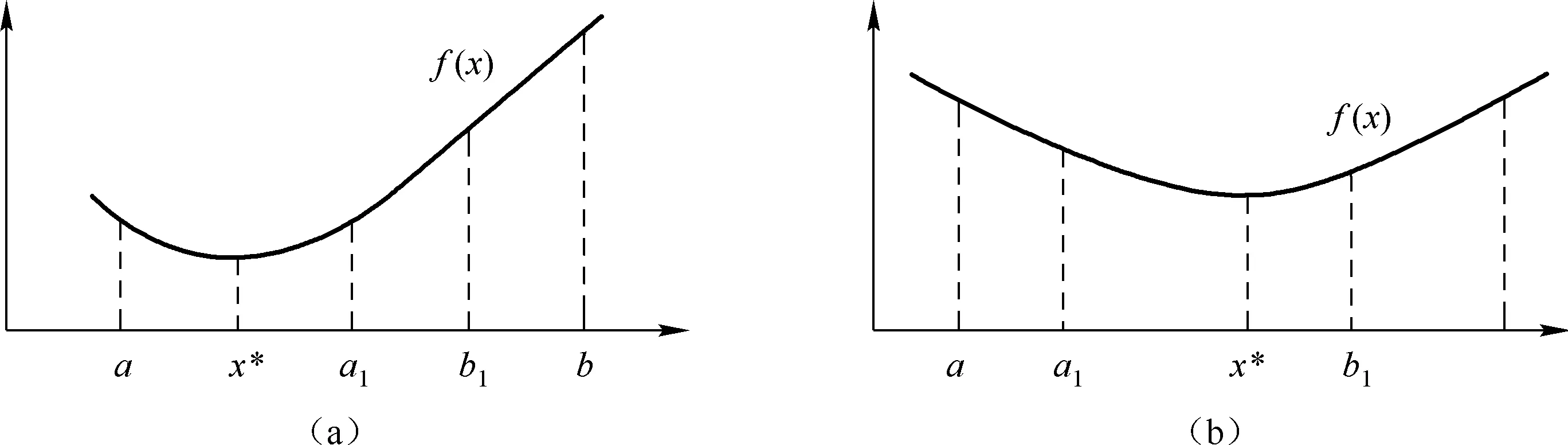
假设目标函数f(x)是区间[a,b]上的下单峰函数(图2),在此区间内有唯一的极小点x*。若在此区间内任取两点a1和b1,并计算(或做试验)得到其目标函数f(a1)和f(b1)。于是,可能出现以下两种情形:
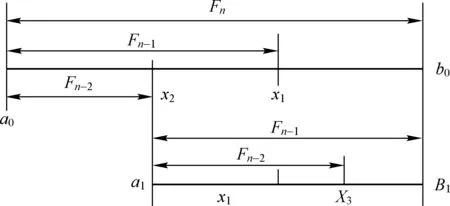
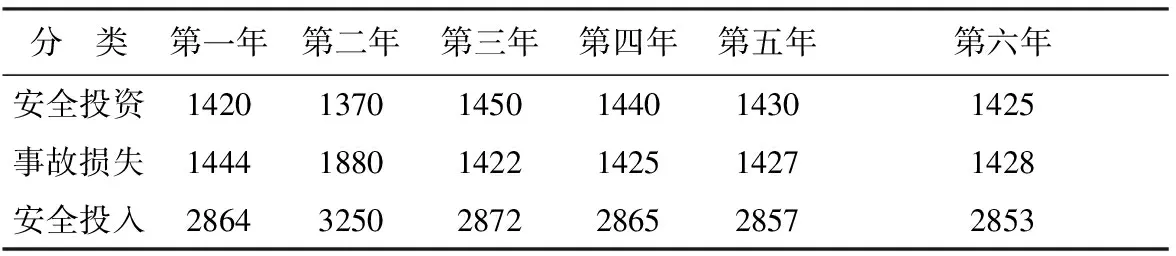
(1)f(a1) (2)f(a1)≥f(b1)(图2-b),这时极小点x*必在区间[a1,b]内。 目标函数为单峰函数(包括下单峰函数和上单峰函数),其中企业安全投入更多体现为下单峰函数,极值点在区间[a,b]内,是十分重要的假设。单峰函数有一个重要的性质:比较区间[a,b]内不同两点的函数值,就可以确定最优值的位置。因此,在区间[a,b]内取两个不同点,并将两个函数值加以比较,就可以把搜索区间 [a,b] 缩小成[a,b1]或[a1,b],如果继续搜索下去,则可在缩小的区间[a,b]内再取一点,求出其函数值并与f(a1)加以比较,进一步缩小搜索区间。试验次数越多,搜索区间越小,从而求出满足一定精度要求的最优解。 (1) 斐波那契数列 斐波那契法是利用斐波那契数列安排试验的单因素优选法。斐波那契数列如表1所示。 表1 斐波那契数列 在表1中,n表示斐波那契数列的下标变量,Fn表示对应下标变量n时的数列值。当n=0,Fn=1;当n=1,Fn=1;…,当n=5,Fn=8。斐波那契数列有一个重要的递推关系式: Fn=Fn-1+Fn-2n≥0 (1) 图2 一维搜索求解非线性规划最优解理论分析图 (2) 利用斐波那契数列安排试验 (2) 式中,δ为一个正小数,称为区间的相对精度。 (3) 斐波那契法安排试验的步骤 ① 确定试验点个数n。根据缩短率δ,用式(2)算出1/δ,然后由表1确定一个最小的n。例如,某试验取定相对精度δ=0.05,1/δ=20,查表1,得最小的n=7,即选定。 ② 选取前两个(年)安全投资试点的位置。设x1为第1个试点,x2为第2个试验点。x1,x2的具体值可根据以下公式计算得到: (3) (4) 说明,x1位于试验区间的右侧,x2位于试验区间的左侧,两个试点的位置是对称的。斐波那契法是按数列中Fn-1与Fn、Fn-2与Fn的比值来确定试点的,故又称为分数法。 ③ 在x1,x2两点上做试验,并比较两点的目标函数值f(x1)和f(x2)的大小。若f(x1)比f(x2)好,则说明x1为较好点,并可判断最优值位于区间(x2,b0),取a1=x2,b1=b0。缩短的区间长度为Fn-1,根据对称试验的特点,显然第3个试点x3应在x1的右侧,按公式(3),得: (5) 若f(x1)比f(x2)差,说明点x2是好点,可判断最优值位于区间(a0,x1)。取a1=a0,b1=x1,缩短的区间长度为Fn-1,由对称试验特点可知第3个试点x3应位于x2的左侧。按公式(4),得: ④ 进行第3个试点x3的试验,与前次好的试验点数比较,可以继续缩小试验区间。重复以上过程,直到满足试验精确度要求为止。 图3 运用菲波那契法确定前两年安全投资点图解 某新建煤矿进行安全投资决策。根据国内同类煤矿的安全投入经验,该规模煤矿的安全投资每年为1370万元。该煤矿为了减少安全投入,最优化安全投资及安全投入,决定在若干年内优选出本煤矿的安全投资和安全投入的数值,试验范围定为1290~1500万元,试验精确度要求10万元。一般认为,试验精确度是指经过试验范围的大小。 用斐波那契法安排实验,其过程为:本例要求安全投资的精确度为10万元,为使试验方便,试点应以整数为单位,因而特选定试验区间长度为某个Fn,故由表1取F7=21,即n=7。试验区间[a0,b0]为[1290,1500]。 第1个试点x1,第2 个试点x2分别由式(3),式(4)确定。 即该煤矿正常生产第一年、第二年安排安全投资1420万元和 1370万元,每年年末评估当年的事故损失,这两年的事故损失分别是1444万元和1880万元。因此,这两年安全投入(实验结果)分别是2864万元和3250万元,如表2所示。可见,x1,x2两点安全投入结果表明,x1比x2点好(2864<3250),因而舍弃区间(a0,x2)。 表3 某煤矿若干年安全投资与安全投入优选分析表 备注:安全投入(实际实验结果)=安全投资+事故损失。说明这里的实验实际是真实的计算结果。 新的试验区间为(1370,1500),即设a1=1370,b1=1500。按照斐波那契法对称试验特点,可知第3个试点x3应在x1的右侧,由式(3)计算x3=1450(万元)。 即该煤矿第三年安排安全投资1450万元,年末评估当年各类事故总损失为1422万元。因此,该年的安全投入是2872万元,如表3所示。点x3的安全投入结果表明,点x1比点x3好(2864<2872),试验区间缩小为(1370,1450)。 确定试点x4=1440万元,即该煤矿第四年安排安全投资1440万元,年末评估当年的事故损失为1425万元,因此,该年的安全投入是2865万元。试验结果是点x1比点x4好。 再确定试点x5=1430万元,如表2,年底核算当年事故损失为1427万元,安全投入(实验结果)为2857万元。 同理,经过5个(年)试验,证明该煤矿安全投资在1420—1430万元时,安全投入最少,安全效果最好,达到了试验精确度的要求。 第六年可取该区间的中点1425万元,年末评估当年的事故损失为1428万元,因此,该年的安全投入基本已达到最小2853万元,如表3所示。当然,随着煤矿开采深度,煤矿需要的安全投入会增加,依然可以运用此法寻找新的生产条件的最优安全投资和安全投入。 (1) 在煤矿安全投资和安全投入与经济效益的关系不能用函数表示出来的情况下,根据非线性规划的基本概念和理论,运用非线性规划问题、斐波那契直接一维搜索优化法的基本思路和方法,可以求解煤矿的最优安全投资和安全投入。 (2) 运用非线性规划问题、斐波那契法直接一维搜索优化的方法,适用于不能用函数关系表示煤矿的安全投资与效益之间的关系时,如何确定煤矿的最优安全投资问题,可以确保煤矿在若干年内就能寻找出本企业的最优安全投资量。 [1] 徐汝华. 浅析安全投入与经济效益[J]. 煤矿安全,1997(8):40-41. [2] 陈宝智. 企业投入的安全经济效用及边际效用[J]. 中国安全科学学报,1998(2):67-70. [3] 刘祖德. 安全经济投资和最优安全水平[J]. 地质勘探安全,2000(4):26-29. [4] 李广华,曹薇. 谈企业安全与安全投资[J]. 水利电力劳动保护,2000(2):35-36. [5] 江正峙. 浅述安全投资与企业经济效益关系[J]. 城市燃气,2003(12):23-25. [6] 孔留安, 李武. 我国煤炭企业安全投入与生产安全问题研究[J],煤炭学报,2006(2):72-75. [7] 辛嵩,程卫民. 煤炭企业最佳安全投资的边际分析[J]. 辽宁工程技术大学学报,2003(8):576-577. [8] 陈晓红,吴双芝. 安全投资项目技术经济指标的研究[J]. 中国矿业,2006(6):18-21. [9] 董炎. 我国煤炭上市公司安全投入与经济效益研究[D]. 太原:山西财经大学,2014(6):25-36. [10] 孙凯. 煤矿企业安全投入与安全效益研究[D]. 青岛:山东科技大学,2006(5):12-21. [11] 姜俊俊. 安全投入与安全经济效益研究[D]. 合肥:安徽理工大学,2010(5):22-25. [12] 马川川. 基于灰色关联分析的煤矿安全投入研究[D]. 昆明:昆明理工大学,2014(4):22-34. [13] 石稳稳. 煤炭企业安全投入与决策研究[D]. 昆明:昆明理工大学,2012(4):15-41. [14] 运筹学教材编写组. 运筹学[M]. 北京:清华大学出版社[第3版],2005. [15] 郭月心. 运筹学[M]. 广州:华南理工大学出版社[第五版],2012.2.2 斐波那契数列及其安排试验

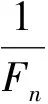
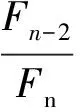
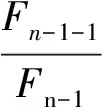
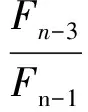

3 斐波那契法的应用实例
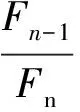
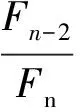
4 结论
