后张法预应力钢绞线伸长量计算与现场量测控制
2017-03-18赵杰
赵杰
摘要: 预应力钢绞线伸长量偏差是衡量预应力张拉控制是否符合设计要求的一项关键指标,其张拉伸长量(包括理论伸长量和实际伸长量)的准确计算和量测,是控制伸长量偏差的主要依据。本文将结合工程案例,对预应力筋理论伸长量分段计算方法进行探讨,并总结理论伸长量的几项影响因素,通过准确的计算为张拉控制提供有效的参考依据。
Abstract: The elongation deviation of prestressed steel strand is a key index to measure whether the prestress tension control meets the design requirements. The accurate calculation and measurement of stretching elongation (including theoretical elongation and actual elongation) is the main basis for controlling the elongation deviation. In this paper, combined with engineering cases, the theoretical calculation method of prestressed tendon elongation is discussed. And the theoretical extension of several factors is summarized to provide effective reference to tension control by the accurate calculation.
关键词: 预应力;理论伸长量;张拉力;量测
Key words: prestress;theoretical elongation;tension;measuration
中圖分类号:U45 文献标识码:A 文章编号:1006-4311(2017)05-0106-04
0 引言
在预应力混凝土结构中,预应力施加过小或过大都会对混凝土结构造成损坏。预应力筋长期受荷载作用的影响,始终处在过高应力状态中,与造成结构裂隙的荷载极为相似,都是没有明显征兆的破坏现象,对结构稳定和安全使用构成了极大的威胁。从另一方面来讲,由于预应力荷载过大,混凝土结构的反拱度随之增大,继而导致预拉区的混凝土开裂的可能性也随之增大,最终也将发展成为危害结构稳定性的主要因素。而如果预应力荷载过小,混凝土结构往往会承载力达不到设计要求,开裂等结构缺陷,同样也会直接破坏结构的稳定性和安全性。由此可见,预应力荷载越接近设计值,对混凝土结构的安全性和稳定性越有利。对混凝土构件施加预应力时,须根据钢绞线伸长量偏差来调整张拉力的大小,以免造成结构破坏。这就需要准确计算预应力钢绞线的理论伸长量,并严格按照设计要求准确测量其实际伸长量。
本文在工程实践中,以30m预应力混凝土箱梁为例,提出一套准确测量预应力钢绞线实际伸长量以及准确计算其理论伸长量的工法,以准确地校核施加的预应力是否满足设计要求,减少施加的预应力与设计要求的预应力差异。
1 工程实例
霍阿公路HATJ-4标霍林郭勒特大桥上部结构为预应力连续箱梁,单根钢绞线直径Фs15.2mm,钢绞线标准强度fpk=1860MPa,钢绞线面积A=140mm2,弹性模量Ep=1.95×105 MPa。设计钢绞线每端工作长度为65cm,锚下控制应力为бcon=0.75fpk=1395MPa。30m预制箱梁中钢束均采用两端张拉,且应在横桥向对称均匀张拉,张拉顺序为N1、N3、N2、N4。预制箱梁锚具采用M15型及其配套设备,管道成孔采用波纹管,其技术参数见表1。
2 划分计算段落
先按图1~图3对整束钢绞线进行分段再计算其伸长值。
2.1 工作长度
工具锚到工作锚之间的长度,图1中工作段长度是650mm。
2.2 波纹管内长度
第一步:将图1分解为图2;第二步:将图2分解为图3,平曲线与竖曲线重合部分以角度较大者为分段点。
以边跨非连续端钢束N1为例计算。
N1的BF段设计总长度为15.458-0.65=14.808m,E点为钢绞线起弯点。
EF(直线段)=2.663m,
DE(曲线段)=α×π×R/180=5×π×45/180=3.927m,
BD=14.808-2.663-3.927=8.218m。
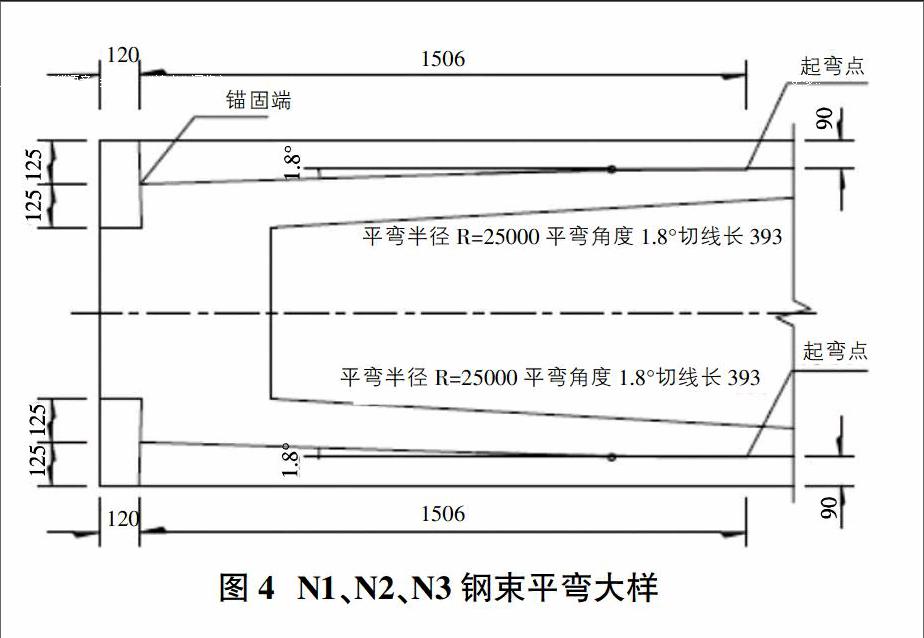
因N1的BC段为曲线筋平弯和竖弯重合部分,BC(曲线段)长度=1.506m(查阅设计图纸图4所得)。
CD段为连接BC段和DE段的直线段,CD(直线段)8.218-1.506=6.712m。
3 计算过程
《公路桥梁施工技术规范》中关于箱梁正弯矩预应力计算公式如下:
预应筋伸长值ΔL通过计算公式(1)获得:
ΔL=■(1)
在式(1)中,“ΔL”表示“各分段预应力筋的理论伸长值(mm)”,“Pp”表示“各分段预应力筋的平均张拉力(N)”,其计算公式为下式(2),“L”表示“预应力筋的分段长度(mm)”,“Ep”表示“预应力筋的弹性模量(Mpa)”,“Ap”表示“预应力筋的截面面积(mm2)”。
Pp:■(2)
在Pp的计算公式(2)中,“P”表示“预应力筋张拉端的张拉力”,将钢绞线分段计算后,为每分段的起点张拉力,即为前段的终点张拉力(N);“μ”表示“预应力筋与孔道壁之间的磨擦系数”,只在管道弯曲部分考虑该系数的影响”,“θ”表示“从张拉端至计算截面曲线孔道部分切线的夹角之和”,分段后为每分段中每段曲线段的切线夹角(rad);“x”表示“从张拉端至计算截面的孔道长度”,分段后为每个分段长度或为公式(1)中L值; “k”表示“孔道每束局部偏差对摩擦的影响系数(1/m)”,管道内全长均应考虑该影响。
公式(1)可以得出,钢绞线的弹性模量Ep是决定计算值的重要因素,它的取值是否正确,对计算预应力筋伸长值的影响较大。所以钢绞线在使用前必须进行测试检测。
公式(2)中的μ和k是后张法钢绞线伸长量计算中的两个重要的参数,其大小有多个影响因素,比如预应力筋类型、表面特征,管道的成型方式、管材质量,弯道的角度、位置,波纹管安装方式等等,在实际操作中各项因素变动幅度较大,甚至有些因素具有不确定性,无法对其变化进行准确预测,因此对摩擦系数的控制主要取决于施工中对各节点参数的控制精度。
3.1 工作长度伸长量计算
张拉时预应力筋的工作长度(mm),应为下料长度减去图纸给定的千斤顶工作长度加上实际的千斤顶工作长度;图纸给定的为0.65m,实际为0.435m(千斤顶长度0.34m,工具锚厚度0.055m,限位板厚度0.04m)。计算时不考虑θ、μ,采用《公路桥涵施工技术规范》(JTG/T F50-2011)中关于预应筋伸长值ΔL的计算按照公式(1)计算:
根据锚下(张拉)控制力为Δk=0.75 fpk =1395MPa,计算千斤顶张拉力P=1395×140=195300N(每根);
根据公式(1)计算工作长度(AB)段的伸长量:
ΔL工作长度=■
ΔL工作长度=6.22mm
3.2 波纹管内钢绞线长度伸长量计算
①计算波纹管内长度分段伸长量前需准备的数据。
张拉控制力=195300N,预应力钢绞线截面面积是140mm2,预应力钢绞线弹性模量是195000MPa,由设计图纸可知:K=0.0015,μ=0.25,X取分段长度m。
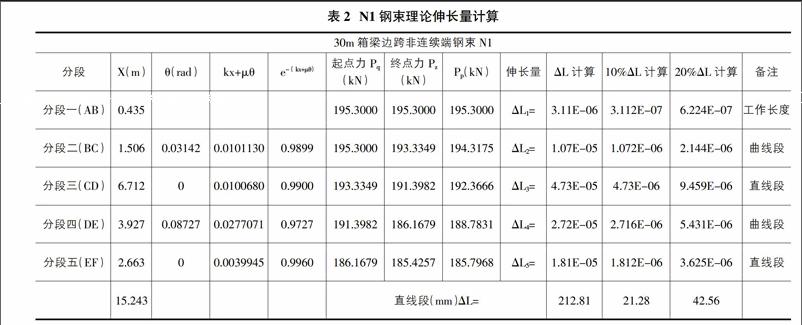
②N1钢束理论伸长量计算見表2。
3.3 预应力筋理论伸长量
△L=(△LBC+△LCD+△LDE+△LEF)×2+△LAB
从上述案例可以看出,理论伸长量的计算方法是目前来看比较精确的计算方法。实测伸长量的在允许误差±6%左右浮动时,应该采用该方法精确计算理论伸长量计算值,如果张拉参数控制不当,将为工程埋下质量隐患,甚至造成工程返工,浪费成本和资源。
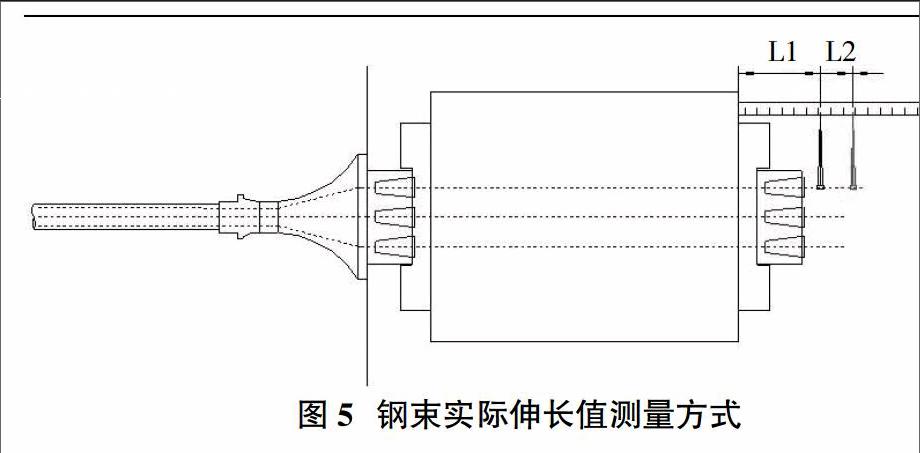
4 张拉时钢绞线实际伸长量的测量方法
当前工程领域有几种有效的钢绞线实际伸长值的测量方法,其中直接测量张拉端千斤顶活塞伸出量的方法多见于实际操作中。但是这种方法在具体操作中容易出现测量误差,因为张拉到10%σk时,钢绞线受力,用钢管敲紧的工具锚端夹片滑向内侧;在张拉到20%σk时,借助夹片对千斤顶的伸长量测量10%~20%σk的伸长量,所得结果往往比实际伸长值多出1~2mm。如果以测得的结果作为0%~10%σk的伸长量,则0%~20%σk张拉控制段内钢绞线伸长量的总误差将是2~3mm。在20%σk张~100%σk的张拉段内,夹片不断滑向内侧,若此时计算最小值滑动量下单端钢绞线伸长量,虽然张拉力符合要求,但是其测量误差将达到3~4mm,若两端同时张拉,误差值将达到6~8mm。因此,通过测量千斤活塞的方法进行张拉钢绞线伸长量的测量和计算,所得到的结果通常比钢绞线实际伸长量偏大。
测量钢束实际伸长量时,可以不使用量测千斤顶活塞伸出量的方法,采用量测钢绞线绝对伸长值的方法,前者测得的伸长量必须兼顾工具锚处钢束回缩及夹片滑移等影响因素,而直接通过测量千顶活塞的伸出量,则会出现较大的误差,如果较长的钢绞线必须进行分级张拉时,更为繁琐。推荐采用图5所示的测量方法。测量时,先在钢绞线上固定一个标尺,用标尺量测分级钢绞线的长度,各段量程累计的伸长值即为初应力与终应力之间的实测伸长值。
5 夹片回缩量补充张拉
张拉并持荷完毕后放松千斤顶使其回弹。在回弹过程中,夹片式锚具将会变形,造成锚下控制应力损失,基于《公路桥涵施工技术规范》中关于锚具回缩量的控制标准是不超出6mm,实际执行时往往因为锚具生产厂家的结构设计不同,锚具回缩量通常都在3~6mm之间,因此张拉并持荷完毕后,千斤顶回弹时需要再将各段钢绞线拉长3~6mm,以弥补夹片回缩量造成的应力损失。
6 结束语
本文仅针对理论伸长量的精确计算方法进行了一定程度的分析讨论,具体操作时建议将通过本方法得出的计算值作为与实测伸长量的对比依据,以此来衡量张拉是否到位,是否存在异常情况,并深入分析异常工况的成因。分析异常原因时注意避免一些不确定性的影响因素。
①原材料的波动会造成预应力筋的弹性模量随波动。
②施工队伍人员的操作质量波动会造成孔道每米局部偏差对摩擦的影响系数波动。
③波纹管质量、存放时间和锈蚀程度不同的变化会造成孔道壁与预应力筋的摩擦系数变化。
④张拉应力的变大会造成预应力筋的截面积逐步变小,但理论伸长量中的AP采取一恒定值与实际不符,该要素会导致理论伸长值减小,无法为衡量张拉操作的准确性提供客观依据。
⑤可以采用量测钢绞线绝对伸长值的方法,对钢束实际伸长值进行测量,避免工具锚处钢束回缩及夹片滑移等影响。
参考文献:
[1]JTG/T F50-2011,公路桥涵施工技术规范[S].人民交通出版社.
[2]周水兴,等.路桥施工计算手册[M].人民交通出版社.
[3]呼和浩特至乌兰浩特(省道101线)霍林郭勒至阿力得尔段公路两阶段施工图设计[M].
