基于多元线性回归的边坡加固工程快速估价模型研究
2017-03-18赵东谢佩瑜
赵东++谢佩瑜


摘要: 边坡工程广泛存在于道路、桥涵及厂区周边,其存在的安全隐患不容忽视,是各类工程中的重点和难点部分。为预防边坡的滑坡、坍塌等灾害的发生,需进行边坡的加固。在可行性研究边坡加固方案的选择阶段,工程师需要根据各加固方案的主要工程量快速估算方案的造价,对边坡方案进行经济性的比选。通过Eviews软件对不同边坡加固设计方案的主要工程量数据样本进行了多元线性回归,给出了适用于不同设计方案的统一造价快速估算模型。经过检验后表明,模型总体回归显著,各解释变量显著,不存在序列自相关。与真实造价对比后模型精度满足估算要求,具有很强的适用性。
Abstract: The slope engineering widely exists in roads, bridges and plant areas, the hidden danger which existed in is not allowed to ignore. Its a important and difficult part of all kinds of engineering. In order to prevent the happening of the slope landslide, collapse and other disasters, engineers need to reinforce the slope. In feasibility study of slope reinforcement conceptual design selection stage, engineer needs to select the cost of all designs according to the main quantities of the design as soon as possible. In this article, sample datas of different slope reinforcement designs have been carried on the multiple linear regression according the Eviews software, The unification cost estimation model are given to adjust different kind of designs. After model tests, it is showed that the model overall regression, the explanation variables are significantly, there is no autocorrelation sequence. After compared with real datas, the precision of the model satisfies the requirement of estimation, which has strong suitability.
關键词: 边坡加固;多元线性回归;快速估价
Key words: slope strengthening;multiple linear regression;fast cost estimation
中图分类号:U418.5+2 文献标识码:A 文章编号:1006-4311(2017)05-0103-03
0 引言
边坡受到外界条件变化或各类因素的影响,其原有的力学平衡被打破,会导致沿着剪切面的整体滑动或者坍塌,进而造成重大的经济损失和人身伤害。为避免此类事故的发生,需进行边坡加固方案的设计。
在可行性研究阶段对方案的选择和确定过程中,不仅需要对各类方案进行详细的设计论证,也需要对各方案的经济性进行分析和论证,技术及经济的论证结果的正确与否,直接关系到项目建设的成败,关系到工程造价的高低和投资效果的好坏[1]。
边坡加固方案的设计主要包括锚杆的设计及坡面的设计,而锚杆的深度及材料种类选择取决于坡面的地质情况,如坡面的土壤岩石类别,整体基岩的深度等。坡面的设计也有格构梁、浆砌片石、喷射混凝土等多种方式。而在方案设计阶段造价人员一般无法得到十分准确和详细的工程量和单价信息,且边坡方案组合较多,这些影响因素都会给各方案的造价估算带来困难。
基于以上现实需求,本文选取了边坡加固方案设计阶段比较确定的数据样本,包括锚杆的重量、坡面的体积及每米钻孔的费用。通过对不同方案组合的以上样本数据进行多元线性回归分析,得到了具有很强适用性的回归方程。
1 多元线性回归快速估价模型的建立、求解和检验
1.1 数据来源、指标选取及模型建立
边坡加固的费用主要包括钻孔费用、锚杆的费用及坡面的处理费用。其中钻孔的费用主要取决于土壤和岩石的类别。锚杆的费用主要取决于锚杆的深度和材质。坡面的处理费用主要取决于采用哪种坡面处理方式[2]。针对分析以上的影响因素,本样本数据来源选取了某5090m2边坡加固项目的施工图设计阶段的设计方案组合,组合1和组合2分别构成24个设计样本及各设计样本的单位面积预算造价,其中钻孔单位长度费用考虑了粘土、砂砾、砾石、卵石等不同的地质条件和各两种软硬程度;锚杆重量考虑了钢筋、钢绞线两种材质及各两种深度的工程量;坡面处理体积考虑了喷射混凝土、格构梁及浆砌片石三种不同做法及各两种厚度的工程量。(如表1)
建立模型的过程是按上表得到的数据采用最小二乘估计法(OLS)进行多元线性回归分析,得到边坡单位面积造价(y)及各自变量钻孔单位费用(x1)、锚杆重量(x2)、坡面处理体积(x3)的回归方程。在Eviews软件中对以上样本的48组数据进行回归分析,得到由一个因变量y和3个自变量x1、x2、x3组成的多元一次线性函数,常数项为随机误差,即为多元线性回归模型[3]:
■=1.58x1+1.49x2+0.65x3-21.98(1)
OLS回归结果如表2所示。
1.2 模型的检验
1.2.1 拟合优度检验
测定多元线性回归线对样本观测值的拟合程度,采用多重判定系数R2来表示,该系数具体定义为:
R2=■=1-■=1-■(2)
其中,TSS为总体平方和(total sum of squares),ESS为回归平方和(explained sum of squares),RSS为剩余平方和(residual sum of squares)。■■表示回归值,■表示观测均值。
R2作为判定系数,表示在多元回归过程中,解释变量对因变量的解释比例,比例越大代表该回归模型可以解释的部分越多,模型越精确。R2的取值在(0,1)范围内,越接近1表明擬合程度越高。由OLS回归结果(表2)可以看出,本回归模型多重判定系数R2=0.98337,表示初步模型回归曲线对观测值的拟合优度高。
1.2.2 F检验
在多元回归中有多个解释变量时,需要对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出推断,即F检验。该检验所用的方法,在数理统计上属于假设检验,验证模型y=?茁0+?茁1x1+?茁2x2+…+?茁kxk+?着中的参数是否显著不为0。检验的零假设为,H0:?茁1=?茁2=…=?茁k=0,检验统计量,F=■。其中,它在零假设下服从自由度为(k,n-k-1)的F分布。若F大于临界值F?琢(k,n-k-1),则拒绝零假设,认为在显著性水平下,因变量对自变量有显著的线性关系,回归方程是显著的;反之则不能拒绝原假设,认为回归方程不显著。
本模型中由OLS回归结果(表2)可以看出,当置信度取为0.05时,F检验统计量的伴随概率P(F-statistic)也小于0.05,表明了该初步模型总体回归显著,与观测值拟合度高。
1.2.3 t 检验
t检验也称参数显著性检验,思路是在多元回归中分别检验当其它解释变量保持不变时,测定各个解释变量对因变量是否有显著影响。如果每一个回归系数都通过了t检验,说明模型中的每一个自变量都是显著的。未通过显著性检验的系数所对应的变量,应结合实际情况考虑将其剔除。
本模型中由OLS回归结果(表2)可以看出,当置信度取为0.05时,x1,x2和x3对应的t检验统计量的伴随概率P均小于0.05,则表示模型选取的三个解释变量都显著。本回归模型通过参数显著性检验。
1.2.4 异方差检验与处理
在得到初步模型之后,我们继续在Eviews中对模型进行异方差检验(White检验)。结果如表3。
从表3 White检验结果(1)中可知,此时的F检验统计量的伴随概率P(F-Statistic)小于置信度0.05,则F检验显著,存在异方差。在Eviews中采用WLS方法消除异方差,得到如果如表4。
由表4可知,此时F检验统计量的伴随概率P(F-Statistic)远大于置信度0.05,则模型无异方差。
在此基础上,我们对异方差消除后数据进行第二次OLS回归,得到结果如表5。
故修正后的模型为
y=1.58x1+1.51x2+0.61x3-11.24(3)
1.2.5 自相关检验
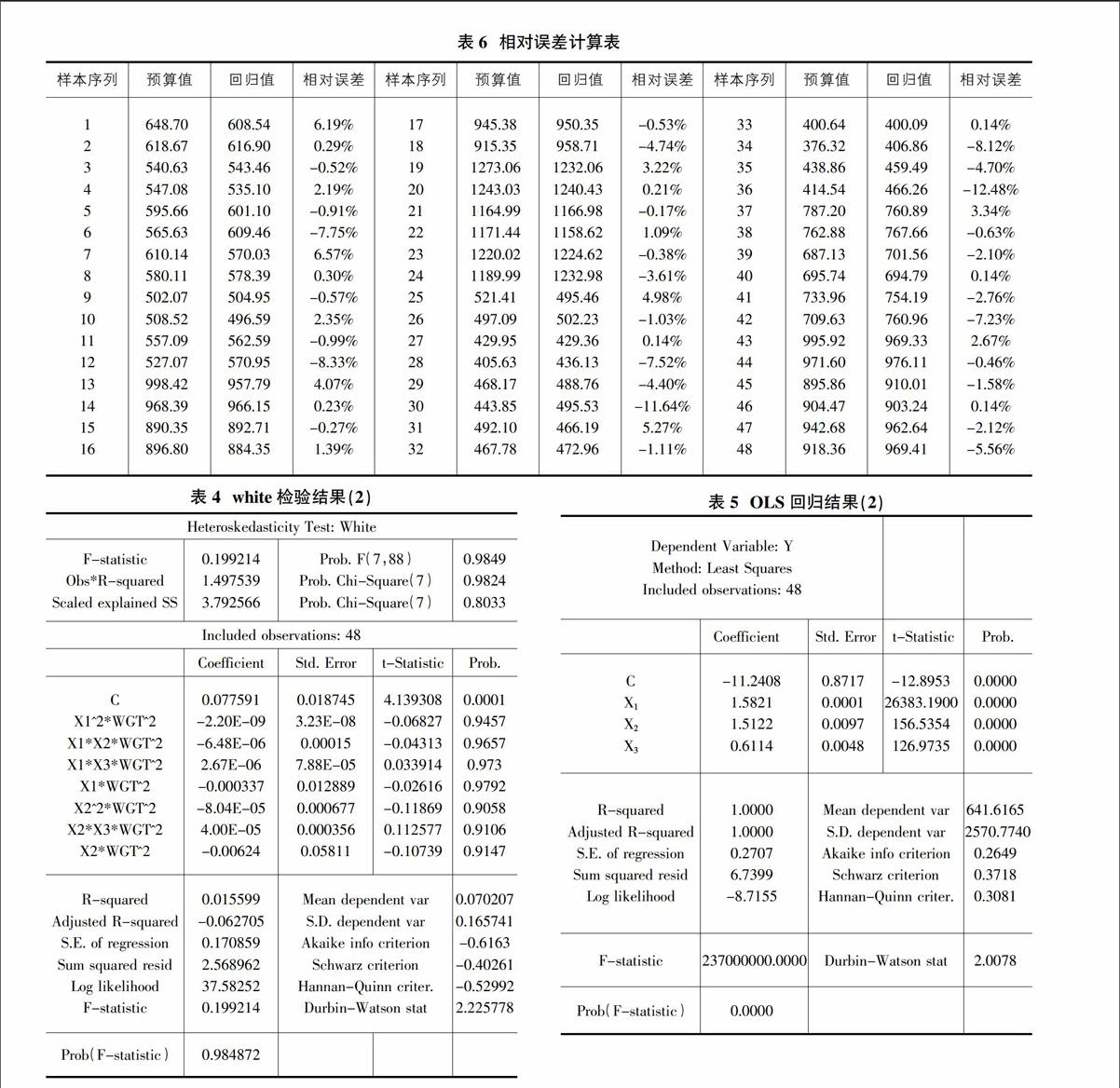
在显著性水平?琢=0.005条件下,通过查阅DW表可知,dU=1.674 2 多元线性回归模型的相对误差分析 将48组样本数据带入回归模型可得到的每平米边坡加固造价的回归值,将回归值与各样本的每平米预算造价值进行对比。由于预算造价来源于施工图工程量的计算,在不考虑设计变更和其他索赔和签证的基础上,仅就方案本身而言,预算价基本等同于边坡加固工程的实际造价,因此,利用公式?着=(预算值-回归值)/(预算值)*100%[4]求出各组样本数据回归值与预算值的相对误差,该相对误差可基本满足用于模型误差的判断。 在工程的可行性研究阶段,投资估算误差率应控制在±10%以内,由表6相对误差计算表得出的48组样本相对误差平均值为3.06%,满足方案比选阶段的投资估算对于误差范围控制的要求。 3 结论 技术经济的论证和比选是可行性研究阶段方案评价和选择工作的重要组成部分,本文对边坡加固方案设计中考虑的重点内容进行了详细的分析工作,对影响造价的重要参数样本进行了多元线性回归,得到的模型总体回归显著,各解释变量显著,不存在序列自相关。与真实造价对比后模型精度满足估算要求,且各参数在可行性研究阶段均较容易获取,模型运用简便,因此本模型对可行性研究阶段的边坡加固方案的经济性比选工作有着很强的适用性。 参考文献: [1]建设工程计价(2014版)[M].北京:城市出版社,2014:109. [2]聂欣岩.干砌石护坡与混凝土护坡在堤防加固中的应用比较[J].水利工程建设,2006(16):38-39. [3]刘严.多元线性回归的数学模型[J].沈阳工程学院学报(自然科学版),2005(1):128-129. [4]吴倩,宋永发.基于多元线性回归的装饰工程快速估价模型[J].建筑管理现代化,2009(23):435-438.
