基于遗传算法的伺服系统PID控制参数整定

姚 禹， 王 博， 高 智*

(1.长春工业大学 应用技术学院， 吉林 长春 130012;2.长春市轨道交通集团有限公司, 吉林 长春 130012)

0 引 言

串并联数控机床伺服系统具有多变量、非线性、强耦合的特点[1-4]，为了满足不同的加工需求，串并联数控机床要求多个控制模块共同协作，故此对应用在其上的控制器要求较高。PID控制器具有原理简单、易于应用、鲁棒性强的优点，在以往数控机床中应用的非常广泛[5-7]。然而，由于串并联数控机床伺服系统控制器要调节电流环、速度环和位置环的多个变量，同时这些变量又存在着并不十分明显的耦合关系，使得串并联数控机床伺服系统极易受负载扰动的影响，若采用常规PID控制，控制器的参数选择则异常困难[8-10]，这使得串并联数控机床的伺服系统难以取得满意的控制效果。

针对这一问题，文中利用遗传算法整定串并联数控机床伺服系统的PID控制参数解决耦合对PID控制参数的影响。通过种群的多样性和较强的寻优能力[11-12]，快速寻优电流环和速度环PID控制参数，实现对串并联数控机床伺服系统PID控制参数的整定，提高伺服系统的控制精度和适应性。通过仿真分析，验证了所提方法具有调节时间短、无超调、鲁棒性强等优点，可改善串并联数控机床伺服系统的控制性能，进而提高串并联数控机床的加工精度。

1 遗传算法的基本原理

基本的遗传算法以包含解集的种群为对象，个体之间依据某种规律进行交叉、变异操作。交叉操作即是两个不同的个体的参数进行交换，而变异操作即是个体上的某一参数按照某一概率发生变化。而后，在生成的新种群中具有优越性能的个体存活下来，适应性差的个体被抛弃。如此循环，达到进化的目的[13-14]，直到性能最优越的个体或满足某一要求的个体出现，进化结束。

文中定义的遗传算法里，每一个个体看成一个特定参数的集合，代表着控制器电流环、速度环和位置环的10个控制参数，个体间经过交叉和变异产生子代个体，然后再把这些个体和子代个体放在一起竞争产生新的2代个体，2代个体重复上述过程产生3代、4代、5代个体等，直到找到一个性能最优越的个体或产生的所有个体都收敛于某一区间，进化过程结束，产生的个体代表PID控制参数调节适当，可将该PID控制参数在串并联数控机床伺服控制器内进行设置。

2 基于遗传算法的PID控制参数整定

2.1 个体的设计与初始化

个体是遗传算法进化过程的基础，个体设计的好坏直接影响遗传算法对串并联数控机床伺服系统PID控制参数的搜索能力和搜索速度。在设计串并联数控机床伺服系统PID控制参数个体时要考虑个体的大小、初始化和多样性等，以确保串并联数控机床伺服系统PID控制参数个体收敛，进而保证遗传算法的收敛性。串并联数控机床伺服系统PID控制参数个体意义见表1。

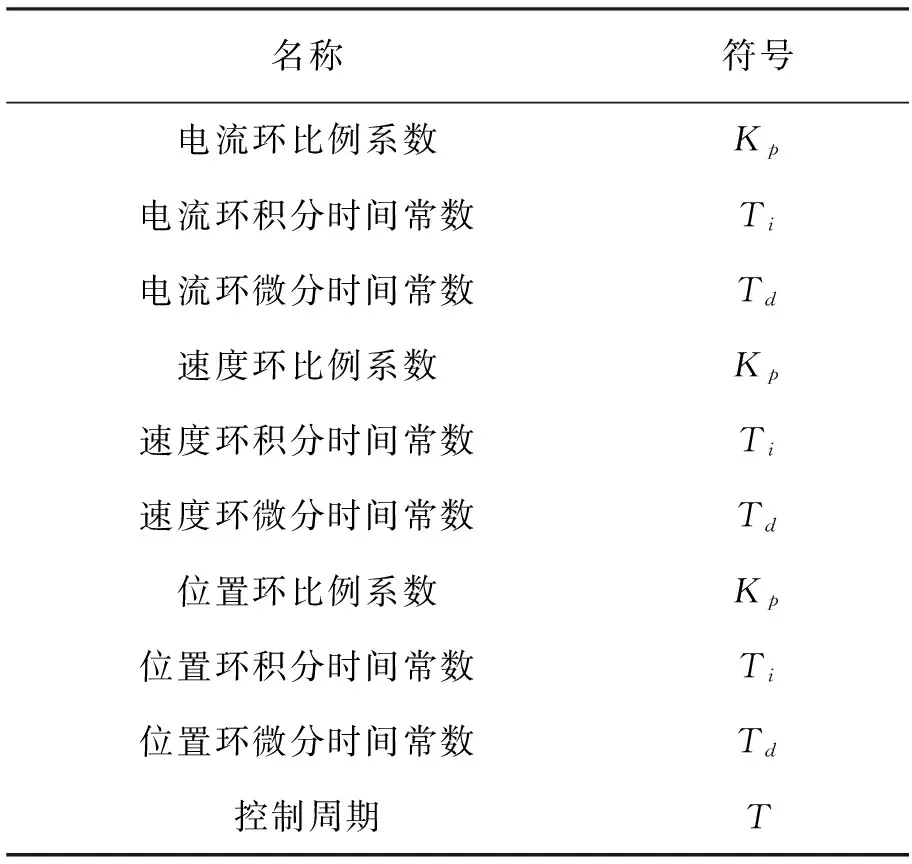
表1 串并联数控机床伺服系统PID控制参数个体意义

2.2 适应度函数的设计

表征伺服系统适应度函数的指标有很多，如超调量、上升时间、调节时间、稳态误差等。即便对于相同的控制系统，只要控制目标不一致，其适应度函数也可以是不一致的。适应度函数可以根据某一性能指标建立，也可以根据多个性能指标，如取各性能指标的加权平均，以系统误差最小为优化目标建立，或以工艺要求建立。但需保证群体中各个个体在优化计算中可能达到或接近达到最优解。

文中根据串并联数控机床伺服系统具有的非线性、强耦合的特点，为了获取满意的过渡过程，在串并联数控机床伺服系统PID控制参数整定过程中，将适应度函数取为目标函数的倒数。这样在利用遗传算法对串并联数控机床伺服系统的电流环、速度环和位置环的PID控制参数进行寻优时，适应度函数值最大的那一组个体参数即为最优的串并联数控机床伺服系统PID控制参数。故此，将误差绝对值、时间积分性能作为最小目标函数，并且为了防止控制过度，加入了其控制输入的平方项。具体串并联数控机床伺服系统PID控制参数整定的最优指标为:

(1)

而后，根据串并联数控机床的加工特点，为了保证加工工件的精度，要求串并联数控机床伺服系统没有超调量。为满足这一要求，在对串并联数控机床伺服系统的PID控制参数进行寻优时，引进了惩罚机制，只要一出现超调量，就立即把超调量作为一目标值，如果：

ey(t)<0

则

(2)

2.3 编码

对串并联数控机床伺服系统中电流环、速度环和位置环的10个PID控制参数进行寻优，每个个体代表了在遗传算法中参数寻优问题时的一个可能解。设样本个数为N，比例系数Kp、积分时间常数Ti、微分时间常数Td变化范围为[a,b]，b>a>0，则比例系数为：

(3)

式中:r----Kp的二进制码。

同理，积分时间常数Ti、微分时间常数Td也做类似的处理。

2.4 遗传算子的选择

在对串并联数控机床伺服系统PID控制参数进行寻优时，需要对群体中的个体进行优胜劣汰的竞争操作即选择，它是在评价适应度函数的基础上建立的。对种群中的个体而言，适应性越高的个体，在竞争中越具有优势，它遗传到下一代中的可能性就会越大；相反，适应性越低的个体，它遗传到下一代中的可能性就会越来越小。

文中在串并联数控机床伺服系统PID控制参数寻优过程中，选用的是赌盘法对遗传算子进行选择，如图1所示。

图1 赌盘法示意图

2.5 遗传算子的交叉

遗传算法中种群产生子代个体的主要途径就是交叉，它是从选中的个体中选择父亲和母亲的基因参数产生新的子代个体。对于每两个基因参数，这种选择机会是平等的。例如在对串并联数控机床伺服系统PID控制参数寻优时，每个个体包含电流环、速度环和位置环的10个PID控制参数，选择一个个体后，随即产生一个二进制数组：1010110010，数字1代表该基因参数是从母亲个体处遗传，数字0代表该基因参数是从父亲个体处遗传。正是这样不统一的交叉，直至进化的结束，才保证了种群的优越性可以遗传给子代个体。

2.6 遗传算子的变异

遗传算法中种群产生子代个体的另一个途径就是变异，但变异是双向的。它既可以产生种群中没有过的优良基因参数，也可以破坏种群中原本就有的优良基因参数。为了保证种群的优越性和多样性，在串并联数控机床伺服系统PID控制参数寻优过程中，需要交叉和变异相互配合，这样可以增强遗传算法的随机搜索能力，共同完成对空间的全局和局部搜索，找到最合适的串并联数控机床伺服系统PID控制参数。

3 基于遗传算法的PID控制参数寻优步骤

针对上文所述的串并联数控机床伺服系统PID控制参数进行寻优，找到性能优越、满足串并联数控机床伺服系统控制精度要求的PID控制参数,利用的遗传算法流程如图2所示。

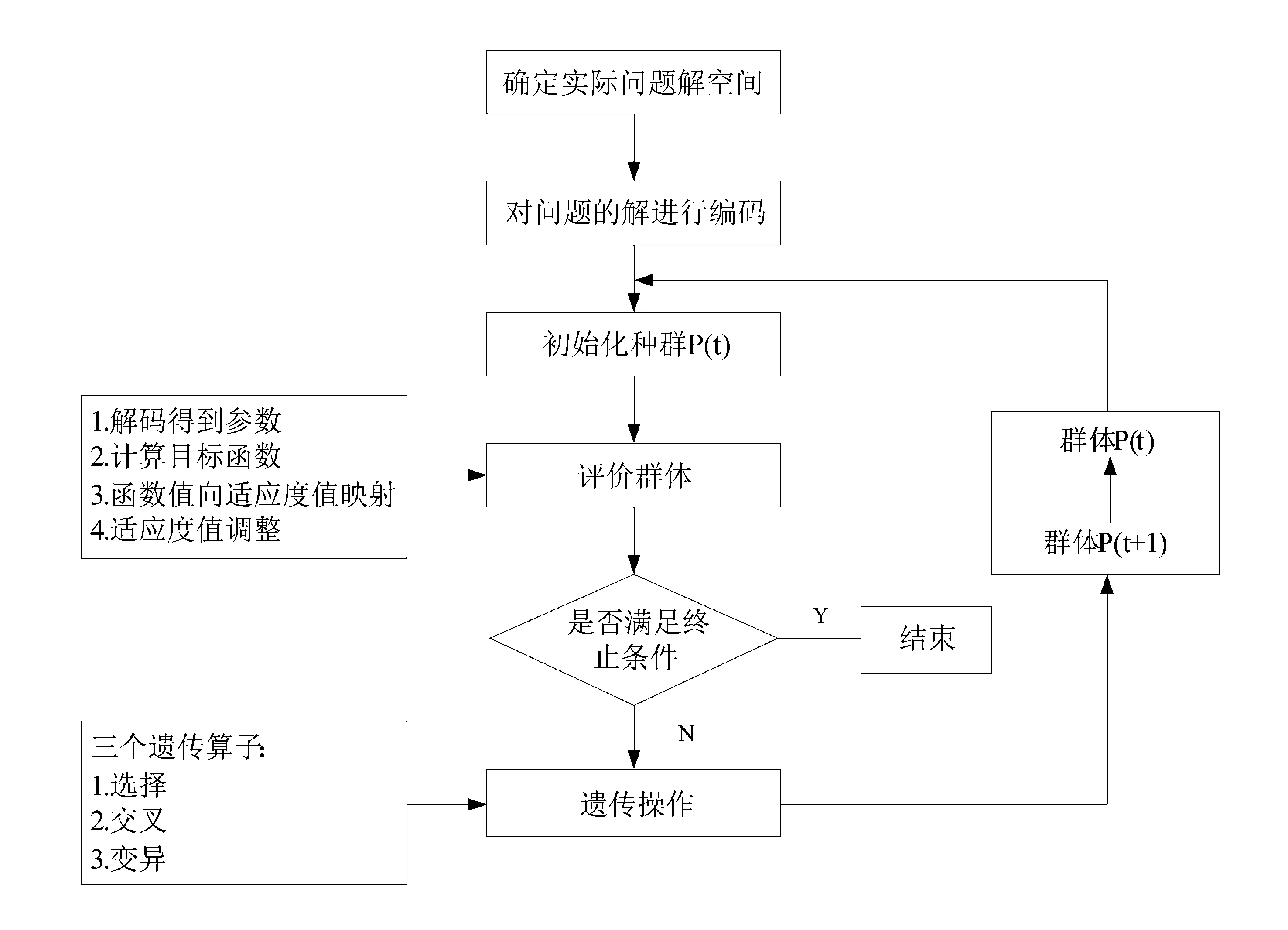
图2 遗传算法流程

4 仿真研究

为了验证所提算法的有效性，基于Matlab仿真环境建立了串并联数控机床双闭环调速系统，如图3所示。

图3 串并联数控机床伺服系统双闭环控制结构图

电流环调节器的传递函数为：

(4)

速度环调节器的传递函数为：

(5)

利用遗传算法对PID控制参数进行寻优，经过100代的优化过程后得到了电流环PID的控制参数结果为:Kp=17.9，Ki=0.93，Kd=0.03；速度环PID的控制参数结果为:Kp=11.42，Ki=0.40，Kd=0.05。

电流环的目标函数曲线和PID控制参数寻优曲线如图4所示。

(a) 电流环目标函数曲线 (b) 电流环PID控制参数寻优曲线

图4 电流环控制性能曲线

给出了速度环的目标函数曲线和PID控制参数寻优曲线，并给出了当输入为阶跃响应曲线时，应用遗传算法寻优后的系统响应曲线,如图5所示。

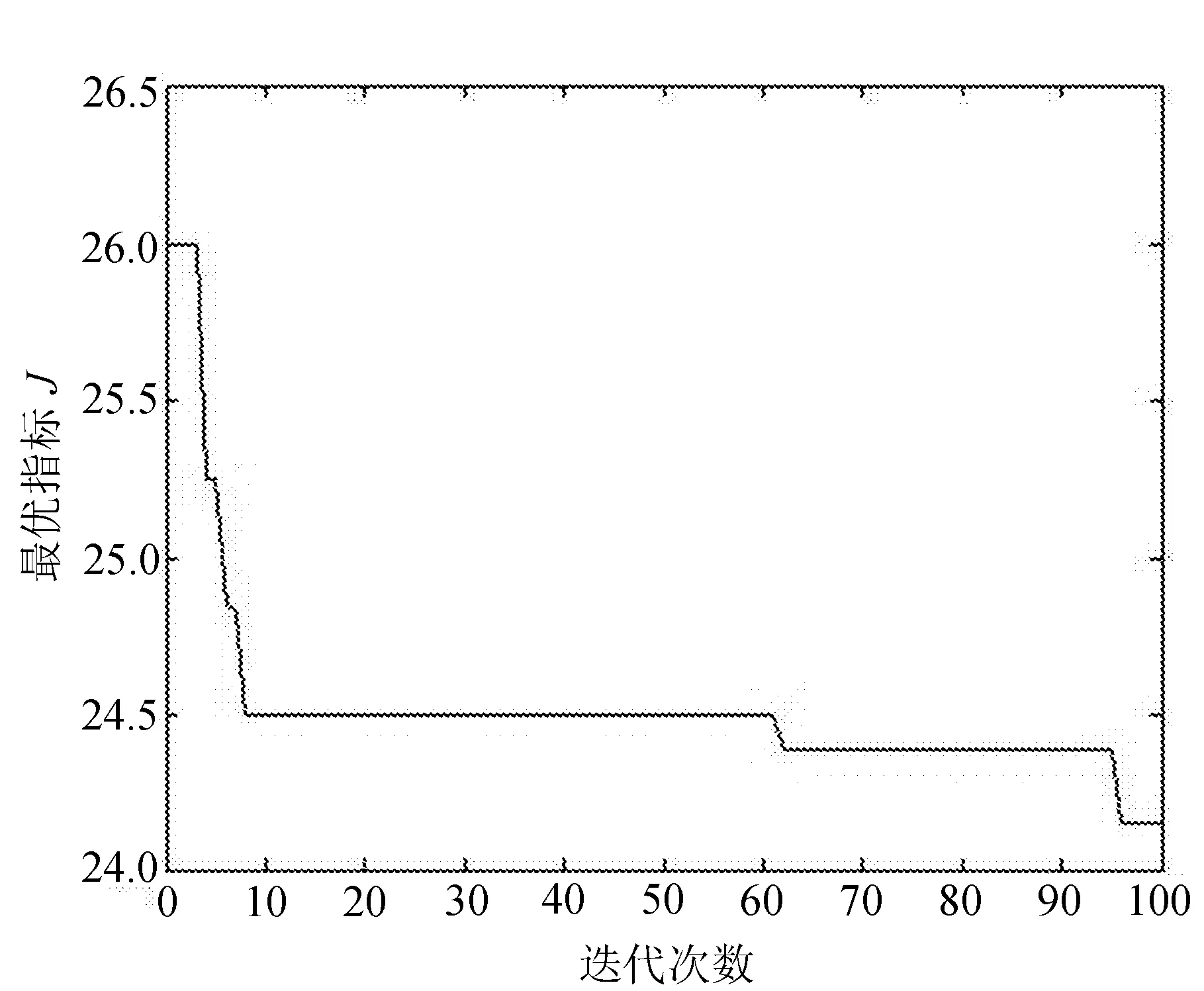
(a) 速度环目标函数曲线 (b) 速度环PID控制参数寻优曲线

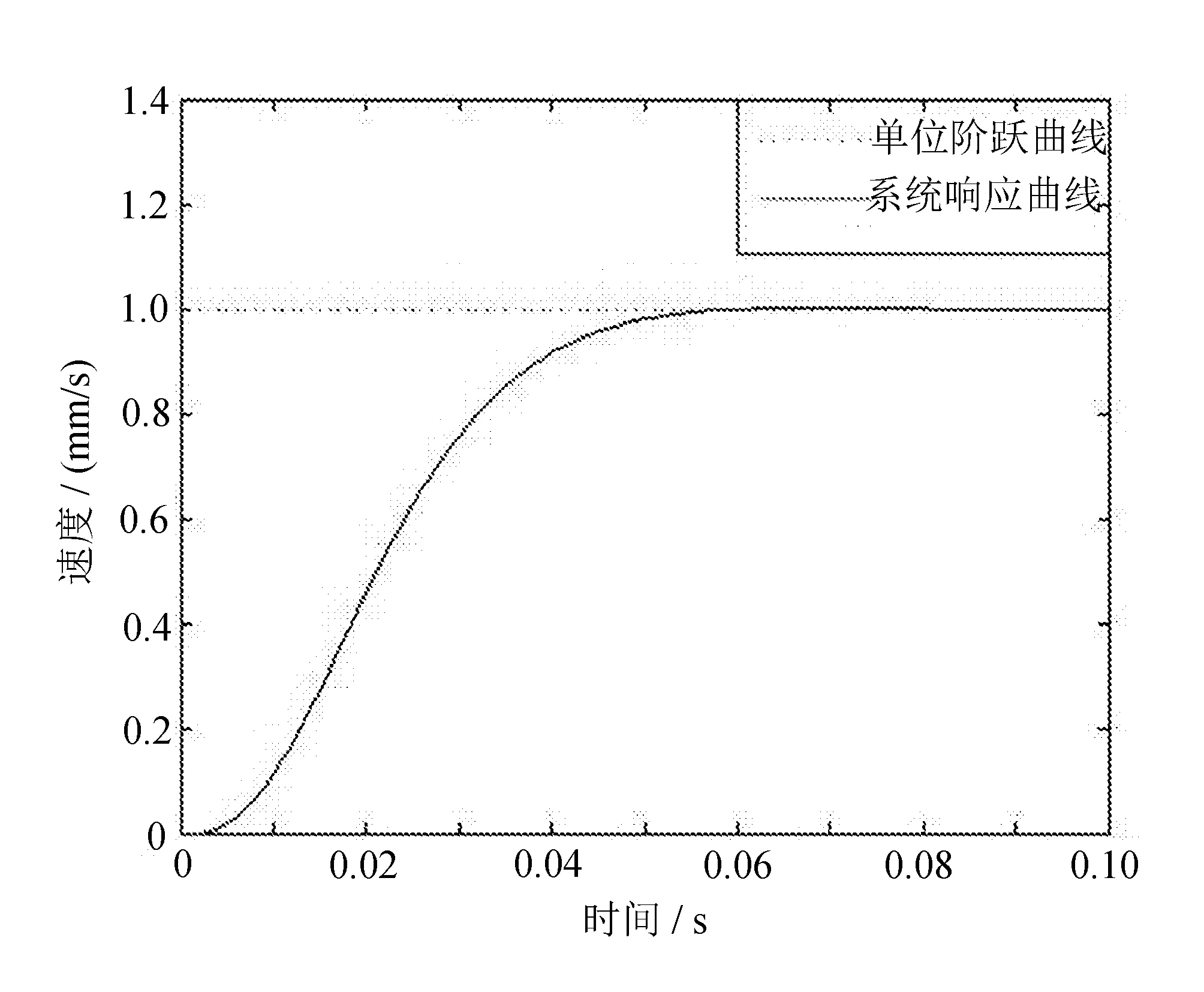
(c) 速度环阶跃响应性能曲线

通过图4和图5的仿真结果分析，文中利用遗传算法对串并联数控机床伺服系统PID控制参数寻优，由于引入了抵制超调量的惩罚因子(见式(2))，可以使图4和图5中的目标函数较小，参数寻优较快，且对串并联数控机床伺服系统控制性能进行阶跃响应仿真时，超调量均为σ%=0(见图5(c))，表明文中提出的基于遗传算法的PID控制参数整定方法可以使串并联数控机床伺服系统的响应时间变短，无超调量，可提高串并联数控机床伺服系统的控制精度，进而改善串并联数控机床的加工性能。

5 结 语

针对串并联数控机床伺服系统具有多变量、非线性、强耦合的特点，提出基于遗传算法的串并联数控机床伺服系统PID控制方法，利用遗传算法快速寻优PID控制参数，实现对PID控制参数的整定。遗传算法可同时完成优化电流环、速度环和位置环控制器的10个控制参数，避免了采用传统方法多次优化才能完成对多个控制器参数整定的繁琐。仿真结果表明，算法响应速度快，无超调，消除了稳态误差，使串并联数控机床伺服系统能获得满意的过渡过程和性能指标，进而提高了串并联数控机床的加工精度。

[1] 蔡赟,张邦成,姚禹.3PTT-2R串并联数控机床动力学耦合特性研究[J].农业机械学报,2015(12):362-369.

[2] 张邦成,王占礼,王义强，等.3-PTT串并联数控机床伺服系统运动学耦合特性研究[J].农业机械学报,2013(11):316-321.

[3] 张邦成,王义强,蔡赟，等.3-PTT串并联数控机床构型设计与位姿分析[J].农业机械学报,2011(9):207-212.

[4] 姚禹,张邦成,蔡赟，等.改进的强跟踪滤波算法及其在3PTT-2R伺服系统中的应用[J].自动化学报,2014(7):1481-1492.

[5] 谭显坤,宿靖波,李雷.PID控制器的模糊优化与参数学习自整定(英文)[J].机床与液压,2013,24:116-120.

[6] 金林骏,方建安,潘磊宁. 一种基于改进的粒子群优化算法的神经网络PID控制器[J].机电工程,2015(2):295-300.

[7] 柴光远,赵鹏兵.模糊自适应PID控制器在液压AGC系统中的应用[J].机床与液压,2010(6):69-71,27.

[8] 黄银萍,唐志勇.工程机械电液比例阀控制系统模糊PID控制器研究[J].机床与液压,2010(13):52-54,18.

[9] Jian SUN, Feng LIU, Jennie SI, et al. Direct heuristic dynamic programming based on an improved PID neural network[J]. Journal of Control Theory and Applications,2012,10(4):497-503.

[10] 周頔.基于遗传算法和模糊神经网络的PID控制器参数优化方法[J].计算机与现代化,2013(9):8-12.

[11] 郝齐,关立文,王立平.基于遗传算法并联机床电机伺服系统控制参数整定[J].清华大学学报:自然科学版,2010,11:1801-1806.

[12] 吴玫,陆金桂.遗传算法的研究进展综述[J].机床与液压,2008(3):176-179,172.

[13] 马永杰,云文霞.遗传算法研究进展[J].计算机应用研究,2012(4):1201-1206,1210.

[14] 张袅娜,李昊林.模糊RBF神经网络PID在汽车定速巡航控制系统应用[J].长春工业大学学报,2017，38(3):237-244.