例谈高考中对正、余弦定理的考查
2017-03-17浙江省玉环县玉城中学蒋克于张夏飞
☉浙江省玉环县玉城中学蒋克于 张夏飞
例谈高考中对正、余弦定理的考查
☉浙江省玉环县玉城中学蒋克于 张夏飞
正、余弦定理是揭示三角形边角关系的两个重要定理,它将三角形的边角巧妙地结合在一起,主要作用是将已知条件中的边角关系转化为纯边或纯角的关系,使问题得以解决;在解题中有着广泛的应用,是高考中的常考知识点,下面介绍正、余弦定理在解题中的一些应用,供参考.
一、判断三角形的形状
正、余弦定理是三角形边、角的混合关系,用定理能将已知条件转化为纯边(或纯角)的关系,从而判断三角形的形状.
即a2sinBcosA=b2sinAcosB.
所以sinAsinB(sinAcosA-sinBcosB)=0,
又A,B∈(0,π),所以sinA≠0,sinB≠0.
所以sin2A-sin2B=0.
因此△ABC为等腰三角形或直角三角形.
即a2sinBcosA=b2sinAcosB.
即(a2-b2)(a2+b2-c2)=0,
所以a=b或a2+b2=c2.
因此△ABC为等腰三角形或直角三角形.
判断三角形形状,通常用两种常用方法:1.统一转化为纯角,再判断(如解法1);2.统一转化为纯边,再判断(如解法2).
二、解斜三角形中的有关问题
解三角形是指已知两边一角(或二角一边或三边),求其他三个元素问题的过程,进而求出三角形的三线(高线、角平分线、中线)及周长等基本问题.

由正弦定理,求出b及c,或整体求出b+c,则周长为3+b+c而得到结果;由于本题是选择题,也可用特殊化的办法求解,取△ABC为直角三角形,则周长应为,故排除A、B、C.而选D.
解三角形时,有时可用正弦定理,也可用余弦定理,同时合理运用三角函数公式,如同角三角函数的基本关系等,解题时应注意用哪一个定理更方便、简捷.
三、解决与三角形面积有关的问题
例3△ABC的内角的对边分别为a,b,c,已知a= bcosC+csinB.
(1)求B;
(2)若b=2,求△ABC的面积的最大值.
解:(1)由已知及正弦定理,得sinA=sinBcosC+sinC· sinB.①
又sinA=π-(B+C),
故sinA=sin(B+C)=sinBcosC+sinBsinC.②
由①②及C∈(0,π),得sinB=cosB.
(1)正弦定理和余弦定理并不是孤立的,解题时要根据具体题目合理运用,有时还需要交替使用.(2)条件中出现平方关系多考虑余弦定理,出现一次式,一般要考虑正弦定理.(3)在求三角形的面积时,通过正、余弦定理求一个角,两边乘积,是一种常见思路.
四、在解决实际问题中的运用
正、余弦定理在实际生活中有着极其广泛的应用,对经过抽象、概括最终转化为三角形中的边、角问题的实际应用题的求解十分有效,下面举两例,以飨读者.
1.“海上营救”问题

图1
例4如图1,某舰艇在A处,测得遇险渔船在北偏东45°距离10海里的C处,此时得知该渔船正沿北偏东105°方向,以每小时9海里的速度航行,舰艇时速为21海里.问舰艇朝什么方向前进可以最快营救渔船?所需时间是多少?(方向精确到1°)
解:设所需时间为t,则AB=21t,CB=9t,∠ACB=120°.
由余弦定理得(21t)2=102+(9t)2-2×10×9tcos120°.解得
2.“台风预报”问题
例5在某海滨城市附近海面有一台风,据监测,台风中心位于城市O(如图2)的东偏南向300 km的海面P处,并以20km/h的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?
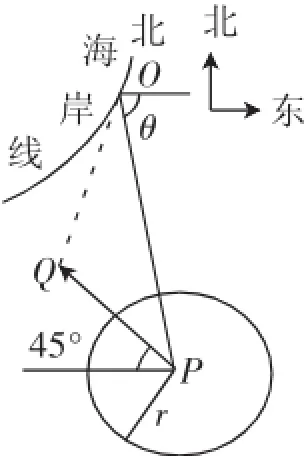
解:设t小时该城市开始受到台风的侵袭,
此时OQ≤10t+60.
由于PO=300,PQ=20t及cos∠OPQ=cos(θ-45°)=cosθ·
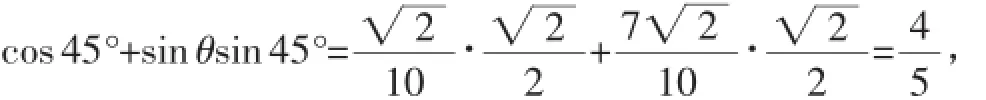
故12小时后该城市开始受到台风的侵袭.
五、在求解二面角时的运用
在立体几何的问题中,涉及一些边长的平方和关系时,常常会联想到余弦定理.
例6如图3,在四面体ABCD中,若AB2+CD2=BD2+ AC2,试求AD与BC所成的角的大小.
分析:将AB2+CD2=BD2+AC2通过移向得CD2-BD2=AC2-AB2,可转化为在两个三角形中进行处理.不妨将等式两边都加BC2,得CD2+ BC2-BD2=AC2+BC2-AB2,与余弦定理有点相似,所以可以试着用余弦定理处理.
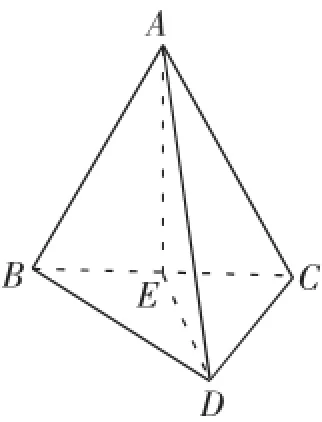
图3
解:由题设得CD2+BC2-BD2=AC2+BC2-AB2.用余弦定理上式即为2AC·BCcos∠ACB=2CD·BCcos∠BCD.
所以ACcos∠ACB=CDcos∠BCD.过A作AE⊥BC于E,过D作DE′⊥BC于E′,所以CE=CE′,E与E′重合,从而AE⊥BC,DE⊥BC.故AD⊥BC,即AD与BC成90°角.
六、在求解方程组时的运用
有些方程组的结构特点与余弦定理的结构相似,因此可以想到构造图形,运用余弦定理解决.
图4

图5
七、在三角不等式中的应用
当要证明的不等式中含有余弦或具有一定的余弦定理的结构时,可以考虑是否使用余弦定理.
证明:因为2R(abcos C+bccos A+cacos B)=abc·
又由余弦定理,得R(a2+b2+c2)=abc·
总之,解题离不开方法的迁移,思路的联想和知识的交融,只要我们在学习时,注意各种公式,定理的顺用、逆用和变形应用,变换角度,纵横联想以及多考虑知识之间的联系,就可以达到化抽象为具体,化繁冗为简单,活学活用的效果.
