试谈变式教学在高中数学中的运用
——以一道高考题为例
2017-03-17湖南省衡阳县职业中专李祖祥
☉湖南省衡阳县职业中专 李祖祥
试谈变式教学在高中数学中的运用
——以一道高考题为例
☉湖南省衡阳县职业中专 李祖祥
变式教学是高中数学教学最重要的教学手段之一,也是高中教师熟悉的教学手段,起到融合各知识点以及知识体系的作用.优秀的老师往往能通过变式训练题组,以点带面,不但能减轻教学负担,还能达到非常好的教学效果.在这种教学模式下,学生学习积极性高,主动性强,课后回味变式,还意犹未尽.笔者通过一道高考题的变式教学实践,粗略谈谈关于变式教学在高中数学中的运用.
案例:在Rt△ABC中,点D是斜边AB的中点,点P为线段CD的中点,则
A.2B.4C.5D.10
该题结构简单,但考点不明,如何确定解题方向呢?
一、解法赏析
解法1:考虑到有直角三角形载体,我们可以建系,用解析法求解.
以点C为坐标原点,建立平面直角坐标系,如图1所示,
设A(4a,0),B(0,4b),则D(2a,2b),P(a,b).
因为|PA|2=9a2+b2,|PB|2=a2+ 9b2,|PC|2=a2+b2,所以=10.
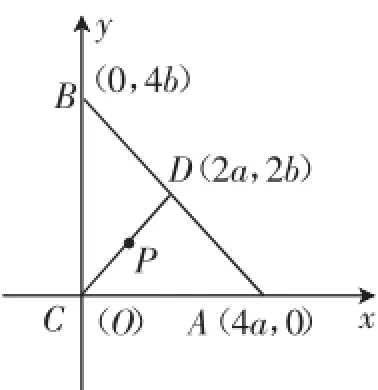
图1
解法2:作为选择题,可将直角三角形特殊化,以等腰直角三角形为载体,计算更简单.解题过程略.
解法3:考虑到目标式的结构及中线特点,应用中线长定理应该也是不错的选择.
中线长定理是关于三角形三边和中线长度关系的欧氏几何定理.其文字表述为:三角形一条中线两侧所对边的平方和等于底边一半的平方与该边中线的平方和的2倍.
如图2所示,设△ABC的三边长分别为a,b,c,边BC,AC,AB上的中线长分别记为ma,mb,mc,则


图2

图3
中线长定理两次出现在人教版课标教材的习题中(一次在解三角形,一次在直线方程),应该引起足够重视,其证明方法多样,本文不再叙述,下面应用结论直接解题.
如图3所示,|AB|=2|CD|=4|PD|=4|PC|.
在△PAB中,应用中线长定理,有|PA|2+|PB|2=2(|BD|2+ |PD|2),
所以2(|PA|2+|PB|2)-|AB|2=4|PD|2,.
所以|PA|2+|PB|2=2|BD|2+2|PD|2=10|PC|2.故选D.
二、变式拓展
如果改变点P在CD上的位置,同样的目标式会有什么样的结果呢?
在Rt△ABC中,∠C=90°,如图4,若△ABC所在平面内的一点P满足,则(1)当λ=1时

图4
按照高考试题的第一种求解思路,不仅计算略显麻烦,而且体现不出小题小做的特点,我们依然采用中线长定理求解.
(1)当λ=1时,点P为△ABC的重心,则PC=2PD.在△PAB中,应用中线长定理,得
2(|PA|2+|PB|2)=|AB|2+4|PD|2
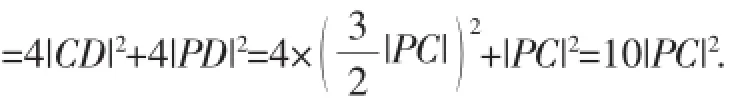
2(|PA|2+|PB|2)=|AB|2+4|PD|2=4|CD|2+4|PD|2=[λ2+(-λ-2)2]|PC|2.
题目虽然得到解决,但总觉得解第(2)小题太麻烦,还是计算,向量作用不明显.我们试图将中线长定理与向量知识结合在一起求解.
解法2:(2)由解法1知,|PA|2+|PB|2=2(|PD|2+|DC|2).
选准考点知识,轻松快捷解题,这应该成为试题研究的一个重要方向.很多试题,解题方向多样,一般化虽然是重点,但不一定是最优的.优化解法,既节省考试时间,又能训练思维,一举多得.
三、几点思考
1.变式教学中鼓励学生主体参与
现代课程观认为,教学活动是师生共同探求知识的过程,是教师、学生、教材、环境等诸多因素相辅相成的动态成长的构建过程,教学活动要充分体现学生的个性,充分落实学生的主体地位,以促进学生的发展为目标.因此,教师将原本学生无从下手的试题引导学生主体参与变式,变式的呈现具有小步子、层层推进、螺旋上升的特点,鼓励学生呈现不同的思维过程,促使学生思维的广度得以延伸,思维的深度得以挖掘,并让学生触及高中数学解决最值问题的思想与方法.在教学内容完成度上,教学设计时已经考虑到了有可能来不及,即使预设了几种变式题型,也无法预料学生的想法及其思考和表达所需的时间.在“教学内容的完成度”与“学生思维的提升”间选择,显然选择学生思维的提升,因为学生思考和表达的过程就是其思维呈现的过程,也是自我反思修正的过程.因此,我们应该积极鼓励学生主体参与,才能更好地促进思维发展.
2.变式教学中优化变式教学策略
如何才能将变式教学做得更有实效些?这需要教师优化变式教学的策略,需要充分发挥学生的主体参与,引导学生进行自主变式,鼓励学生主动探究,激发更多的学生积极参与课堂.关注学生个体差异,科学合理地呈现学生设计的变式,使变式问题层层递进、螺旋上升,让学生有序有向地思考分析问题,使各层次学生思考之后各有所得.关注学生的思维发展,学生根据题目原型迁移类比遇到过的类似问题,联想所学数学的基本知识、概念、性质、定理、思想方法等,让难以解决的问题扩大其“最近发展区”,能收获设计问题、解决问题的成就感,激发学习的积极性,能有效地训练学生思维创造性,教师可以有意识地引导学生从变化中寻找问题之间的联系,从变化中发现问题不变的本质,从不变的本质中探究变化的规律,从而深刻理解变式中的知识与思想方法,培养思维的深刻性.关注问题交流,对学生的课堂参与给予足够的激励和引导,尊重学生的课堂主体地位,注意倾听学生的声音,建立起和谐平等的师生关系,在融洽的氛围之中将数学教学做得更有实效些.
