导数应用问题中解题方向的确定
——从函数图像入手
2017-03-17山东省肥城市第一高级中学贾传强
☉山东省肥城市第一高级中学 贾传强
导数应用问题中解题方向的确定
——从函数图像入手
☉山东省肥城市第一高级中学 贾传强
导数是处理函数问题的有力工具,在求函数的单调区间、极值、最值等有着广泛的应用,对于常规问题,我们可按程序化的思路求解.对于某些创新型的问题不知从何入手时,若借助函数的图像分析,常可顺利找到解题的方向.下面举例说明.
例1已知函数f(x)=ex(x2+ax+a).
(1)求f(x)的单调区间;
(2)求证:当a≥4时,函数f(x)存在最小值.
解析:本题第(1)问属于常规题型,按导数法求函数单调区间的处理程序即可顺利解答,其中对导函数正、负的判断可借助导函数的图像来实现.具体过程如下:
函数的定义域为R,对函数f(x)求导得f′(x)=ex(x2+ ax+a)+ex(2x+a)=ex[x2+(a+2)x+2a].
令f′(x)=0,即x2+(a+2)x+2a=0,解得x=-a,x=-2.
①当-a=-2,即a=2时,f′(x)≥0恒成立,所以函数f(x)的单调递增区间为R.
②当-a>-2,即a<2时,简略图像如图1所示,在区间(-∞,-2),(-a,+∞)内,f′(x)>0,在区间(-2,-a)内f′(x)<0,所以函数f(x)的单调递增区间为(-∞,-2),(-a,+∞),单调递减区间为(-2,-a).

图2

图1
下面对第(2)问的求解进行详细分析.
一、思路分析
因为a≥4,所以-a≤-4<-2,由第(1)问情况③可知,函数f(x)的单调递增区间为(-∞,-a),(-2,+∞),单调递减区间为(-a,-2),函数f(x)的大致图像如图3所示.

图4

图3
若存在x0∈(-∞,-a),使得f(x0)<0,则函数f(x)不存在最小值.
因此若函数f(x)存在最小值,则其大致图像应如图4所示,即在(-∞,-a)内f(x)>0恒成立,且f(-2)≤0,则最小值为f(-2).
根据上述形象分析,明确了解题的方向,即将问题转化为判断在(-∞,-a)内f(x)>0恒成立以及f(-2)≤0.
二、严谨解答
方法1:由第(1)问可知,当a≥4时,函数f(x)的单调递增区间为(-∞,-a),(-2,+∞),单调递减区间为(-a, -2).函数f(x)在区间[-a,+∞)内f(x)≥f(-2)=而4-a<0,所以f(-2)<0.
因为在区间(-∞,-a)内,x2+ax=x(x+a)≥0,所以x2+ ax+a>0,而ex>0,所以f(x)=ex(x2+ax+a)>0,所以当a≥4时,函数存在最小值f(-2).
点评:本解法通过挖掘隐含条件、采用局部判断,即在区间(-∞,-a)内,函数f(x)的正负由x2+ax来决定,从而将陌生问题转化为熟悉的问题,简洁求解.
方法2:由第(1)问可知,当a≥4时,函数f(x)的单调递增区间为(-∞,-a),(-2,+∞),单调递减区间为(-a,-2).函数f(x)在区间[-a,+∞)内f(x)≥f(-2).
由二次函数y=x2+ax+a的性质知,当x→-∞时,x2+ax+ a>0,且ex>0,所以f(x)=ex(x2+ax+a)>0.
所以当a≥4时,函数f(x)存在最小值f(-2).
点评:本解法采用有限与无限思想对函数f(x)的正、负进行判断,方法简单、易于入手,是学生解题中普遍采用的方法.
三、变式演练
(1)求f(x)的单调区间;
(2)若f(x)在[0,+∞)上存在最大值和最小值,求a的取值范围.
本题第(2)问,从形式上来看,与例1如出一辙,例1给出参数范围,证明函数存在最小值.例2是若函数存在最小值,反过来求a的范围.

图5
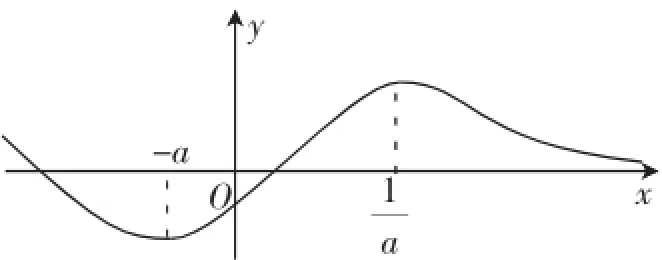
图6
那么当x→+∞时,函数f(x)是否恒为正呢?
方法1:当a>0时,由一次函数y=2ax+a2-1的性质知,当x→+∞时,2ax+a2-1>0,而x2+1>0,所以f(x)=0,则函数在x=0取得最小值f(0),此时应满足f(0)<0,即a2-1<0,-1<a<1.
其实挖掘隐含条件不难发现,函数f(x)只有一个零点,即2ax+a2-1=0,且当x→-∞时,恒有f(x)<0; x→+∞时,恒有f(x)>0,所以其正确的图像如图7所示.
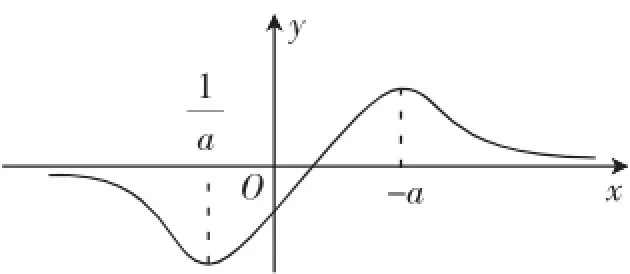
图7

图8
方法2:设x0为f(x)的零点,易知.从而x>x0时,f(x)>0;x<x0时,f(x)<0.
若f(x)在[0,+∞)上存在最小值,必有f(0)≤0,解得-1≤a≤1.结合条件知0<a≤1.
所以当a>0时,若f(x)在[0,+∞)上存在最大值和最小值,a的取值范围是(0,1].
所以a<0时,若f(x)在[0,+∞)上存在最大值和最小值,a的取值范围是(-∞,-1].
综上,a的取值范围是(-∞,-1]∪(0,1].
总之,通过利用导数法求出函数的单调区间、极值、最值后可快速描绘出函数的图像,进而明确了下一步问题处理的方向.但要注意对题目隐含条件的挖掘,如本题中零点的唯一性,以及临界状态的分析,如本题中x→+∞或x→-∞时,函数值的恒正或恒负的情况.
