分类讨论思想在高中数学中的应用探析
2017-03-17江苏省梁丰高级中学黄耀平
☉江苏省梁丰高级中学 黄耀平
分类讨论思想在高中数学中的应用探析
☉江苏省梁丰高级中学 黄耀平
相比于初中阶段的数学教学,高中数学教学显然进入了一个更为高级的阶段.这个阶段的特点并不仅仅表现在知识难度的提高上,更表现在学生学习关注点的扩展和提升上.进入到高中阶段之后,学生们决不能再将目光单一地集中在具体的知识内容之上,而是要将视野放宽,从规律方法的层面上对数学知识进行把握.找到了规律方法,无疑是在数学学习过程中开辟出了一条捷径,从根本上为学习效率的提升注入了动力.因此,着眼规律方法开展教学活动,是高中数学教师应当建立起的高效教学意识.
一、关注分类讨论方法,推进函数问题探究
函数是高中数学的重头戏,其变化方式更是灵活多变.因此,针对函数内容所开展的教学活动向来是很受教师们重视的.学生们如果能够将函数部分的知识内容掌握到位,必将为整个高中数学学习奠定基础,稳固半壁江山.既然函数问题形式多样,内容繁杂,逐个记忆研究自然是不现实的.如果能够找到方法,统一适用,必定可以让函数知识的学习过程事半功倍.
例如,在对函数知识进行延伸时,我为学生们设计了这样一道题目:关于x的方程ax=-x2+2x+a(a>0且a≠1)有多少个解?学生们的初步思路形成都是很顺利的,即分别构造函数y=ax和y=-x2+2x+ a,通过确定两个函数图像的交点个数来得出最后答案.而难点就在于交点个数应当如何确定.由于字母a的存在,使得函数y=ax的单调性并不唯一.为此,就需要分a>1和0<a<1两种情况进行讨论,综合考虑二者结论得出题目的最终答案.经过分别作图(如图1和图2所示)发现,两个函数的交点数量始终为2个,答案得以确定.通过这个练习,学生们找到了借助分类讨论的方法来对函数问题中的不确定部分进行把控的方式.

图1

图2
说到函数问题的难度,很大程度上都会体现在问题内涵的灵活多变上.在很多比较复杂的函数问题中,经常会出现多种方向的可能性.这样一来,学生们的思维就很容易被这些可能性所打乱,造成分析解答的困难.如果学生们能够在函数问题的思考中掌握分类讨论的规律方法,便能坦然面对眼前的复杂局面,冷静分析,针对每一种可能性分别进行有效处理.
二、关注分类讨论方法,推进几何问题探究
分类讨论的规律方法并不仅仅适用于代数类问题,于几何问题当中同样应用广泛.既然是几何问题,就离不开图形的加入,图形之间的位置关系也就成为了很多问题的讨论焦点.然而,很多几何问题当中的条件叙述并不明确,也就为分类讨论方法的使用提供了前提基础.学生们既要善于从已知条件中发现多种可能性的存在,更要善于运用分类讨论的方法全面解答问题.
例如,在一次阶段测验中曾经出现过这样一道平面几何题目:如图3所示,在平面直角坐标系中,有一个点C(1,0),以它为圆心的圆与坐标纵轴相切,一条直线l与该圆相切,切点为点D,且点A(-1,0)在这条直线上.(1)直线l的解析式是什么?(2)直线l上是否存在一个点P,使得△APC是一个等腰三角形?
这道题目的正确率并不高,主要问题都出在第(2)问的解答上.对于△APC中的哪两条边等长,很多学生都是想当然地加以确定,而没有进行分类讨论.经过讲解,学生们意识到,对于这种不确定的题目条件,必须厘清思路,找准分类标准逐一进行讨论,方能保证结论的完整.具体至这道题,就应当根据点P、C、A分别为三角形顶点逐个进行讨论.
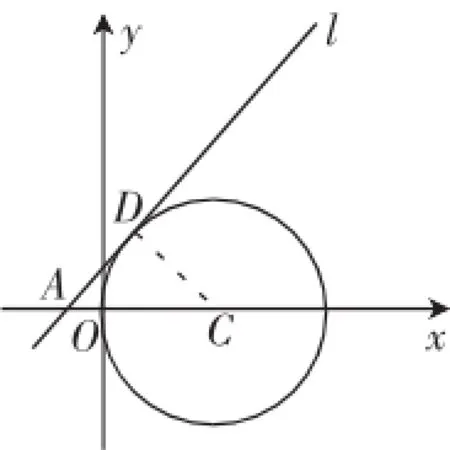
图3
很多比较复杂的几何问题,并不是在图形的层面上独立存在的,而是常常与方程、函数甚至数列等代数问题联系在一起.这样一来,就为当前的几何问题增加了很多分析的难度.特别是在条件氛围比较模糊的时候,学生们必须准确找到关键节点,并以之作为分类依据,对几何问题进行有效分析.
三、关注分类讨论方法,推进数列问题探究
数列问题一直是高中生感到难度很大的数学问题之一.虽然从概念与公式的角度来看,数列问题的内容明确清晰,但是,真正进入到问题解答环节时,便会发现,数学问题的变化方式着实灵活,综合程度也很高,对学生们的思维能力提出了相当强的要求.一方面,学生们要将数列的基础知识掌握到位,融会贯通,另一方面,还要有能力对复杂问题进行条理清晰的分析,将每一种可能都考虑到位.
例如,在数列内容的教学中,我特意引入了如下题目:数列{an}是一个等比数列,它的首项是2,公比是0.5,前n项和是Sn.
(1)请用Sn来表示Sn+1;
很显然,第(2)问是学生们感到困难的地方,要使得条件成立,只需要(k∈N*).又因为Sk+1>k,(k∈N*),所以由Sk<4,要使Sk+1>Sk,(k∈N*)成立,c只能取2或3.到此,分类讨论的标准也就出现了.很多数列问题之所以难度较大,原因都在于分析过程中这种多可能性的存在.意识到这一点,并妥善处理,思路就清晰多了.
对于数列问题的关注,不能仅仅集中在公式与定理的简单应用上,更要训练学生们在繁杂情形之下厘清头绪,寻找分析关键点的能力.当学生们能够站在一定的高度上来审视数列问题,及时发现其中的分析焦点之所在时,也就能够很好地确定解答方向及用力重点,解题过程自然顺利许多.
四、关注分类讨论方法,推进应用问题探究
在高中数学当中,应用问题所占据的比重向来不小.准确解答应用问题,不仅是为了在各类数学考试当中取得理想成绩,更是为了在实践之中检验学生们的知识理解效果,为数学知识的深入探究和继续学习夯实基础.因此,解答应用问题也就很自然地成为了高中数学教学的一个重要组成部分.这也是分类讨论方法的一个典型应用.
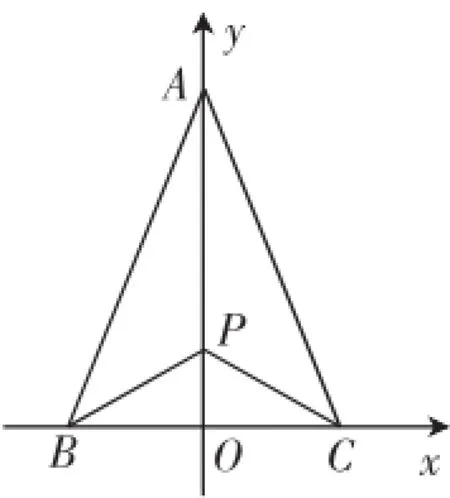
图4
例如,学生们曾经遇到过这样一道应用问题:如图4所示,点A、B、C分别表示三个城市的位置,其中,AB与AC的长度均为13,BC的长度为10.为了能够让这三个城市同时享受到高质量的医疗服务,政府部门计划在BC的垂直平分线上的合适位置规划一个综合性医院,并将这个位置记为点P.那么,如果要使医院到三城市间距离的平方和最小,应当如何确定位置?如果要使医院到三城市间最远距离最小,又应当如何确定位置?第一问的难度较低,第二问的解答则涉及到将点P到三点的最远距离分别表示出来后的处理.若将这个最远距离设为函数g(y),只有将当≥|12-y|时,g(y)<|12-y|时,g(y)=|12-y|两种情况同时考虑,才能保证最后答案的准确性.
由此可见,想要将每一道应用问题都高效解答出来,并不是一件容易的事情.想要灵活应对高中数学当中的应用问题,除了要将具体的知识内容理解到位并灵活运用之外,还要掌握规律性的思想方法,以之应对应用问题当中所出现的各种可能性.应用问题的实践氛围并不同于理论性问题,很多分类讨论的目标是隐藏在应用性的叙述文字当中的,分析难度往往是更大的.将分类讨论方法运用于应用问题解答当中,是师生们应当尤其关注的.
高中数学中的知识数量大,知识难度高,对学生们的学习能力提出了很高的要求.为了妥善应对各种知识内容,学生们必须学会用巧劲儿,从看似杂乱无章的内容要点当中找出共性,提炼总结,得出可以普适于多种类似问题解答的规律方法.这不仅是高效学习数学的有效方法,更是学生们的数学思维能力显著提升的标志.适用于高中数学学习的规律方法有很多,分类讨论只是其中颇具代表性的一种.本文以分类讨论为典型开展论述,就是为了给广大高中师生以启发,以此为切入点,建立起探寻规律方法的意识,大力促进数学教学实效走向强化.
1.宋远娜.“学讲方式”下的高中数学课堂问题串教学的研究[J].中学数学(上),2016(10).
2.沈桂兰.分类讨论思想在数学教学中的应用[J].数理化解题研究.2016(30).
3.朱明安.高中数学分类讨论思想例析[J].上海中学数学.2007(09).
