变式训练是提高学生数学思维能力的有效途径
2017-03-17广东省云浮市云浮中学
☉广东省云浮市云浮中学 赵 华
变式训练是提高学生数学思维能力的有效途径
☉广东省云浮市云浮中学 赵 华
《普通高中数学课程标准(实验)》中写到“培养和发展学生的数学思维能力是发展智力、全面培养数学能力的主要途径,因此高中数学课程应注意提高学生的数学思维能力,这也是数学教育的基本目标之一”.《普通高中数学课程标准(实验)》把提高数学思维能力作为十条基本理念之一.在数学教学中,变式训练是一种传统的、典型的提高学生思维能力的数学教学策略,是广大数学教师在长期的教学工作中总结出来的一种行之有效的教学手段.所谓数学变式训练,是在数学教学过程中对概念、公式、定理及问题等从不同角度、不同情形、不同层次做出有效的变化,使其条件或形式发生变化,本质特征却保持不变.利用变式训练,可以把一个孤立的问题从不同角度向外扩散,并形成一个有规律可寻的系列,帮助学生在问题的解答过程中去寻找解决类似问题的方法、思路,培养学生分析和解决问题的能力,从而提高学生数学思维能力.从知识类型上区分,数学变式可分为概念定义变式、定理公式变式、习题变式三类,习题变式主要包括一题多用变式、一题多变变式、一题多解(证)变式和多题归一(一法多用)变式.下面结合教学实践谈谈在数学教学中如何运用变式训练,提高学生的数学思维能力做一些探讨.
一、变式训练可以增强学生的直觉思维能力
数学直觉思维是非逻辑思维的一类,它没有完整的逻辑思维过程,迅速地对问题的答案作出直接设想、猜测或顿然领悟.著名数学家徐利治教授说过:数学直觉是达到对数学知识真正理解的重要途径.只有这样,才能使相应的内容在头脑中成为“非常直接浅显的”和“非常透彻明白的”,从而真正达到“真懂”或“彻悟”的境界.同时指出“数学直觉是于后天培养的,实际上每个人的数学直觉也是不断提高的”,也就是说数学直觉思维是可以通过训练提高的.实践证明,有效的变式训练能够培养学生的直觉思维能力.
例1求证:等腰三角形底边上任意一点到两腰的距离之和等于腰上的高.
已知:如图1,在△ABC中,AB= AC,CD是AB边上的高,P是BC边上的一点,PE⊥AB于E,PF⊥AC于F.

图1
求证:PE+PF=CD.
对上题进行如下变式:
变式1求证:等腰三角形底边上任意一点到两腰的距离之和为定值.
变式2求证:等边三角形边上的任意一点到另外两边的距离之和为定值.
变式3求证:等边三角形内一点到三边的距离之和为一定值.
变式4求证:等腰三角形底边的延长线的一点到两腰的距离之差是一定值.
几何中的“定值”证明题具有较大的难度.依据例1的原型启发、联想,
运用直觉思维,猜测出变式1、2、3、4题中的“定值”可能是“腰上的高”,即使猜测得不对,还可以把“定值”的猜想范围放宽到腰长、周长、底边上的高等概念上,使证明具有了方向性和目的性.在以上各变式题中,基本图形仍是等腰三角形,只是点的位置的变化.
二、变式训练可以提高学生的抽象概括思维能力
抽象概括是思维的基础,抽象是有层次的,逐步深入的.数学教学活动中,如果能根据学生思维发展水平,利用概念的逐级抽象概括过程,及时向学生提出高一层次的抽象任务,就能不断提高学生的抽象思维能力.变式训练的过程与抽象概括思维的过程基本一致,因为我们在实施变式训练过程中必须遵循目的性原则和层次性原则,这样我们才能有目的地逐层推进,以保证我们的变式得以顺利进行.例如,在学习导数概念时,学生原有的数学认知结构中没有适当的观念与微分相对应,所以需要创设一个学生熟悉的实际情景以引进导数,进而引起对原有的函数的认知结构的扩张,形成导数的认知结构.人教版选修2-2教科书中,通过两个具体的实例,通过计算平均变化率再利用极限而逐步抽象到瞬时变化率.例如,由平均速度到瞬时速度,在具体的教学中,可通过逐步变换问题,区分平均量与瞬时量的差异,以抓住导数概念的本质特征,达到建立抽象概念——导数的目的.这样可使学生感到引入导数概念是自然的、必要的、可行的.该方法既简单又实用,它不仅有利于学生掌握数学知识,而且也有助于提高学生的抽象思维能力.
借助对问题非本质特征的变化(甚至改变问题的结构)而得到新问题的方法,符合数学变式教学的要求.变式的目的就是要让学生在不断变更问题情景或者改变思维角度的情况中,学会从中抽象出问题的本质特征,并逐渐理解抽象的数学对象背后隐藏的深刻思想方法和实质.数学变式教学让学生对问题解决的过程及问题本身的结构有较清晰的认识,使他们能够在不断变化的问题情境中积极思考,这些思考的过程正是学生形成抽象思维能力的过程.
三、变式训练可以提高学生的发散思维能力
一般来说,数学上的新思想、新概念、新方法往往来源于发散思维,它是数学思维能力的一个重要方面,是培养创造思维能力的重要环节.发散思维需要从不同方面考虑解决问题的多种可能性,因而其富于联想,思路开阔,善于分解、组合和引申推广,善于采用各种变通方法.因此,变式训练就成为培养学生发散思维的桥梁和纽带.数学变式训练中,可以通过一题多变或一题多解(证)变式来培养学生的发散思维.
例2已知抛物线y2=2px,过其焦点F作斜率为k的直线交抛物线于A(x1,y1),B(x2,y2)两点,求证
题干条件不变,进行如下变式:
变式1求证:y1y2=-p2.
四、变式训练可以提高学生的逆向思维能力
逆向思维,就是按通常思维的相反方向思考问题的方法,也称为反向思维.在思考数学问题时,顺推不行时可以考虑逆推,直接解决不行时可以考虑间接解决,证明原命题困难时可以考虑证明它的等价命题,通常能起到化难为易的作用.在数学学习中,学生习惯于正向思维,往往忽视逆向思维,如习惯于公式定义、定理的正向运用,而拙于它们的逆向运用,故在教学中应当注重这方面的训练,可通过一题多变中的逆向变式等方式,来培养学生的逆向思维能力.在数学教学中,为了帮助学生从不同的角度理解有关知识要点,可以编制一些“反问题”来训练学生的逆向思维能力.
五、变式训可以提高学生的空间想象能力
一百多年前,恩格斯给数学下的定义是“研究客观世界的数量关系和空间形式的科学”.所谓空间想象能力是人们对客观事物的空间形式(空间几何形体)进行观察、分析、认知的抽象思维能力,空间想象能力反映在:一是能否根据空间几何形体或根据表述几何形体的语言、符号,在大脑中正确想象其直观图.二是能否根据直观图,在大脑中展现出直观图表现的几何形体及其组成部分的形状、位置关系和数量关系,进而能否不借助几何直观,对头脑中已有的空间几何形体进行分解、组合,产生新的空间几何形体,并正确分析其位置关系和数量关系.培养学生的空间想象力是数学教学的主要任务之一.辩证唯物主义认为,任何事物的变化发展都有其内在规律,空间想象能力的提高也是如此,它是逐级向上的,即有明显的层次性.数学教师只有把握好这一规律,并将它有机地渗透到教学实践中去,有针对性地采取得当的教学方法和措施,才能有效地提高学生的空间想象能力.
学生空间想象能力的提高,有不同的途径.可以采用如归纳、类比等方法,也可通过变式训练的教学方式来实现,即通过对图形进行分解、组合与变形,并向基本图形转化,或通过对问题本质的探究,将其引申,变换为相关图形而得到变式问题链,引导学生运用图形的知识和空间想象来解决数学问题,从而培养学生的空间想象能力.
例4让学生根据图2正方体(设棱长为a),回答问题:在图2中,求证:AC1⊥B1D1,在变式图3中,A1C和AB1有类似结论吗?

图2
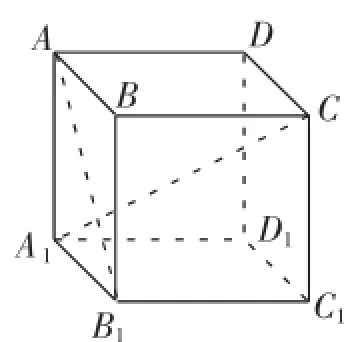
图3
根据这两个结论,你能发现什么规律?
变式1在复合图4中,你能分解出几个标准(变式)这种基本图形?并求证:A1C⊥平面AB1D1
变式2在复合图4中,连接BD,DC1,BC1,求证:平面AB1D1∥平面C1BD,并求这两个平面的距离.
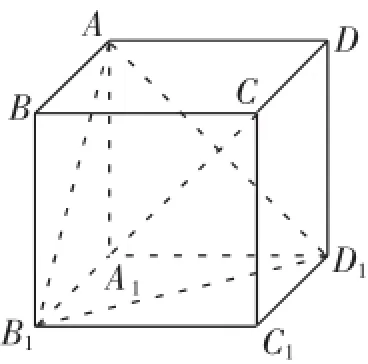
图4
变式3在复合图4中,连接AC和A1C1,求证:对角面ACC1A1⊥平面AB1D1.
需要指出的是,标准和变式图形是相对的,如果把图3当标准,那么图2就是变式.但通常是把比较直观、学生容易理解的图形作为标准图形讲授新知识.至于复合图形是指前两者组合,或同以前学过的基本图形的组合.标准和变式图形是让学生掌握基本知识技能,而复合图形则是培养学生分解基本图形的能力,为解决复杂问题奠定良好的基础.故三结合图形的教学模式对任何水平学校都有指导意义.
综上所述,在数学教学中应用变式训练教学手段,可引导学生多方位、多角度地思考问题,深入理解概念本质,灵活运用定理公式,提高解题的应变能力,能有提高养学生的数学思维能力,同时有利于促进学生创造性思维能力的不断发展.
1.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003.
2.刘长春,张文娣.中学数学变式教学与能力培养[M].济南:山东教育出版社,2001.
3.赵晓楚,周爱东.如何在数学课堂中实施变式教学[J].中小学教学研究.2007(5).
4.蒲大勇,史可富.如何让数学思想落地生根[J].数学通报,2016(3).
5.付佑珊,金宝铮.迁移原理与变式教学[J].数学通报,2016(9).
