利用小波包分析古建筑结构损伤研究
2017-03-17秦堃
秦堃


摘要: 对古建筑结构的损伤进行有限元分析,提出随机激励作用下古建筑结构的小波包能量变化率指标。把古建筑结构梁上各节点的加速度响应信号进行小波包变换来进行损伤定位,该指标对于古建筑结构的损伤比较敏感,能准确判定古建筑结构的损伤位置,损伤程度越大,此指标越大。随后又提出损伤程度的判别方法并验算了其有效性,为研究环境激励下古建筑的损伤预警提供了理论依据。
Abstract: Based on the finite element analysis of the damage of ancient building structures, this paper puts forward the wavelet packet energy change rate index of the ancient buildings under random excitation. The wavelet packet transform is taken for the each node's acceleration response signal of the ancient building structure beam to make a damage localization, whose index is sensitive for the ancient structural damage, can accurately determine the ancient building structure location, showing that the greater the extent of damage is, the greater the index is. Then, the method of judging the degree of damage is put forward and the validity of the method is checked, which provides a theoretical basis for the research on the early warning of the damage of the ancient buildings under the environment excitation.
关键词: 古建筑结构;有限元;小波包;损伤研究
Key words: ancient building structure;finite element;wavelet packet;damage detection
中图分类号:TU312 文献标识码:A 文章编号:1006-4311(2017)07-0109-04
0 引言
损伤识别分为局部损伤和整体损伤两大类。局部损伤和整体损伤两者诊断方法存在较大差异,只有将两者结合起来,才能准确评价复杂结构的健康状况。小波分析被认为是傅里叶分析方法的突破性进展,具有放大、缩小和平移等功能,通过检查不同放大倍数下的变化研究信号的变化特征,有优良的时-频域特性,缺点是高频段分辨率差。小波包变换是小波变换的扩充,能为信号提供一种更加精细的分析方法,将小波分析没有细分的高频部分进一步分解,具有任意的时-频分辨率,因此小波包变换在土木工程结构的健康监测与损伤诊断中具有非常广阔的应用前景。丁幼亮等进行了基于小波包能量谱的结构损伤预警方法研究[1],徐龙河等[2]提出了一种基于结构振动特性的损伤指标定位方法,对空间钢框架支撑结构损伤进行定位分析,于哲峰等[3]进行了基于互相关函数幅值向量的结构损伤定位方法研究。
本文提出小波包能量变化率指标对古建筑结构的损伤识别,把有限元分析得到的梁上各节点的加速度响应信号进行小波包变换,计算该指标进行损伤识别[4]。
1 小波包变换
2 古木结构的损伤识别
2.1 合理的选择小波函数
从消失矩和支撑长度考虑,选择Daubechies小波函数,简记dbN(N为阶次)。时域的分辨和局域性都跟N有直接关系,因此应合理确定Daubechies小波阶次N。
對结构动力响应进行第i层小波包分解,fij表示第i层分解节点(i,j)上结构响应,每个频带内结构响应fij能量[5]:
Eij=∑fij2(j=0,1,2,…,2i)(8)
则结构动力响应f(N,k)第i分解层的小波包能量谱向量Ei:
Ei={Ei,j}=[Ei0 Ei1… Eij … Ei2i-1]T(9)
为衡量小波函数好坏,定义i分解层各频带能量系数系列{Eij}的代价函数M{Eij}。小波包能量谱中各频带能量系数Eij的时频集中程度由代价函数M{Eij}反映。
2.2 合理地选择小波包分解层数
2.4 损伤识别的判定
采用小波包能量变化率进行损伤识别时,Benffey和Montgomery提出了用数理统计方法建立损伤指标阀值的方法[7],目的是设定上限和下限排除干扰带来的误差,若该值大于控制值,可判断结构发生了损伤,同样可设置单边置信区间的统计指标来识别古木结构的损伤。
假设古木结构梁上有n个节点,采用小波包分解,可得到n个小波包能量变化率指标,则置信水平(1-?琢)的单边置信限为[8]:
3 算例
3.1 古建结构损伤的模拟
本文以某古建筑为例,采用Ansys有限元软件对古木结构进行损伤模拟,选取木框架参数如下:木梁长4m,木柱高6m,梁截面尺寸为300×700mm2,柱截面直径500mm,用beam188梁单元模拟木柱、木梁,用combin14单元模拟梁柱的榫卯连接,榫卯连接的弯曲刚度为1×1010kN·m/rad,木材的弹性模量取1×1010N/m2,泊松比为0.25,密度为410kg/m3[10]。柱和基础的连接简化为固定铰支座[11],建立古木结构的有限元模型如图1所示。
在支座1上施加水平方向的随机激励荷载[12],激励荷载的时程曲线如图2所示,获得结构的竖向加速度时程曲线,运用Matlab编制程序计算小波包能量变化率指标。
表1列出古木结构的损伤工况,损伤程度通过折减损伤单元的弹性模量,其中10%、18%、20%分别指损伤单元的弹性模量减少10%、18%、20%[5]。
3.2 选择计算参数
3.2.1 选择合适的小波函数
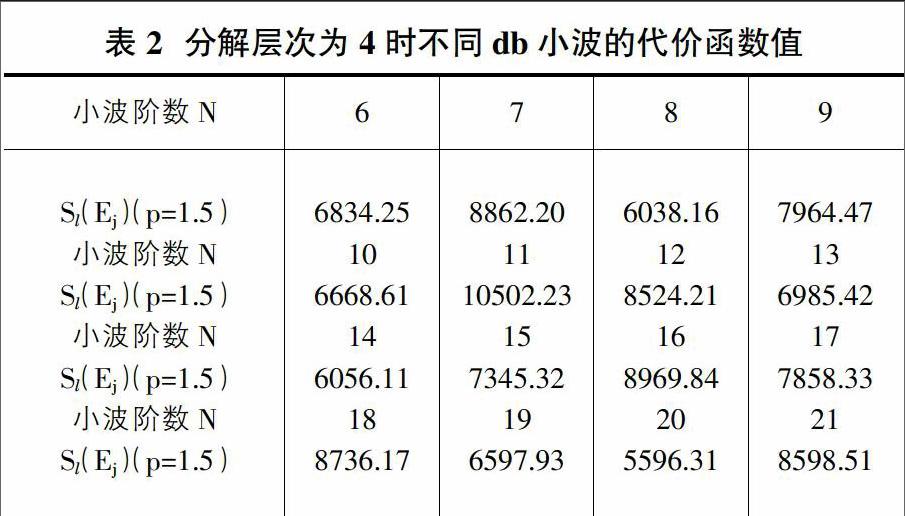
因梁跨中挠度较大,对完好结构梁跨中第31节点的竖向加速度响应进行分析,选择不同阶次Daubechies进行小波包分解,分解层次取4,计算lp范数熵的代价函数如表2所示。通过分析小波阶次为20时,lp范数熵为5596.31,该值最小,因此损伤识别小波函数选择Daubechies20。
3.2.2 选择小波包分解层数
采用Daubechies20对梁跨中第31节点完好状态竖向加速度响应进行小波包分解,分解层次取1~8,计算lp范数熵的代价函数值和计算机计算所用时间如表3所示。通过比较分解层次为4时代价函数值为5596.31,计算时间为0.112秒,代价函数值和计算时间均最小,因此损伤识别小波包分解层次取4。
3.3 损伤识别的判定
本文选择db20小波函数对古木结构梁上各节点完好结构和损伤工况1、2的竖向加速度响应信号进行小波包分解,分解层次取4。采用式(13)求出各节点小波包能量变化率指标,损伤工况1、2的梁上各有9个节点,得出9个能量变化率指标,对这9个指标采用数理统计,求出其均值和方差,假设置信水平为98%,由式(15)求出限值UL,并绘制损伤工况1、2的损伤指标如图3所示。
从图3(a)、(b)看出,节点30、31、32的损伤指标均大于限值UL,可判定节点30、31、32之间存在损伤,正好是梁假定的损伤单元52、53所在位置,与损伤工况1、2所假定的损伤位置完全吻合,可判定在此处存在损伤,在跨中第31节点指标值最大,随着节点离跨中距离越远,指标值越小,说明跨中损伤程度最大,离跨中越远,损伤程度越小,到梁两端时损伤程度最小,这与梁在跨中弯矩最大,最易损伤相符合,此指标可准确判定古木结构梁的损伤位置。比较图3(a)、(b)发现工况2的损伤指标比工况1大,这与工况2损伤程度比工况1大相符合,因而该指标能很好识别古木结构的损伤位置和程度。
同样对该梁采用式(14)计算小波包能量变化率指标,选择与上述相同的小波函数和分解层次,绘制损伤工况1、2的损伤指标如图4所示。
同样从图4看出,节点30、31、32上的能量变化率指标都大于限值UL,可判定节点30、31、32之间存在损伤,与假定的梁损伤单元52、53所在位置吻合,可准确判定古木结构梁的损伤位置。31节点指标值最大,随着节点离跨中距离,指标值越小,说明跨中损伤程度最大,离跨中越远,损伤程度越小,梁两端损伤程度最小,这与梁的受力特征相符合,此指标可准确判定古木结构梁损伤位置。比较图4(a)、(b)看到工况2的损伤指标比工况1大,与假定工况2的损伤程度比工况1大相符合,因此该指标能很好识别结构的损伤位置和程度。
比较图3、图4发现,对同一损伤工况,采用式(14)计算的损伤指标大于式(13)的损伤指标,说明本文提出的损伤指标更能敏感表征古木结构梁的损伤位置,并且损伤程度越大,指标值越大,说明该指标可以定量和定性地判断古木结构梁的损伤。
3.4 判定损伤程度
由图3、图4看出,损伤指标的图形基本相似,只是数值大小有差别。设想若能找到损伤程度和损伤指标间的函数关系,画出其关系曲线,知道了损伤指标,可由此判断损伤程度了。
假设古木结构梁跨中出现损伤,对梁跨中损伤程度10%、15%、20%、25%、30%、35%、40%各损伤工况进行有限元分析,得到相应的竖向加速度信号,由式(14)求出梁跨中的损伤指标——小波包能量变化率指标与置信上限之差,采用Matlab进行数值拟合找到节点31處损伤程度和损伤指标间的函数关系,节点31的损伤指标如表4所示,绘制其函数关系如图5所示。
从图5得出损伤指标和损伤程度的函数关系式为:y =0.0039x2-0.051x+0.671,对某一损伤结构施加随机荷载,获得相应的加速度响应,进行小波包分解,由式(14)求出损伤指标, 可在图5中找到对应的损伤程度。
下面验算该函数关系式的有效性:假设梁跨中损伤程度为18%,对损伤工况3进行数值分析,得到梁上各节点的竖向加速度响应信号,进行小波包分解,绘制损伤指标如图6所示,得到31节点的损伤指标y=1.08,由该函数关系式可逆推出x=18.8%,误差为0.8%,这说明该函数关系式得出的结论比较准确,具有可行性和应用性。
4 结语
通过工程例子,提出了小波包能量变化率损伤识别指标,把随机荷载作用下的古木结构梁上各节点的加速度响应信号进行小波包变换,用此指标进行结构损伤定位。该指标对于古木结构梁的损伤较敏感,可准确判定古木结构梁的损伤位置,本文提出的损伤指标更能表征古木结构梁的损伤位置,该指标随损伤程度的增大而变大。随后又提出损伤程度的判别方法并验算了其有效性,有利于环境激励下某钟楼的损伤预警研究。
参考文献:
[1]滕军,朱焰煌,周峰,李惠,欧进萍,傅学怡,顾磊.基于复Morlet小波变换的大跨空间结构模态参数识别研究[J].振动与冲击,2009(08).
[2]徐龙河,杨冬玲,李忠献,等.空间钢框架支撑结构损伤定位分析[J].天津大学学报,2011,44(7):577-581.
[3]于哲峰,杨智春.基于互相关函数幅值向量的结构损伤定位方法研究[J].振动与冲击,2006,25(3):77-80.
[4]朱磊,张厚江,孙燕良,王喜平,闫海成.基于应力波和微钻阻力的红松类木构件力学性能的无损检测[J].南京林业大学学报(自然科学版),2013(02).
[5]Fook Choon Choi, Jianchun Li,Bijan Samali,Keith Crews. Application of modal-based damage-detection method to locate and evaluate damage in timber beams[J]. Journal of Wood Science. 2007 (5).
[6]李守巨,刘迎曦,吴玉良,何翔,周园π.基于神经网络的建筑结构节点损伤识别方法[J].大连理工大学学报,2003(03).
[7]X. Yang,T. Amano,Y. Ishimaru,I. Iida. Application of modal analysis by transfer function to nondestructive testing of wood II: modulus of elasticity evaluation of sections of differing quality in a wooden beam by the curvature of the flexural vibration wave[J]. Journal of Wood Science, 2003 (2).
[8]Laurence R C,Stephen L Q.Detection of wood decay in blue gum and elm: an evaluation of the resitograph and the portable drill. Jounal of arboriculture, 1999.
[9]趙鸿铁,董春盈,薛建阳,隋龑,张海彦.古建筑木结构透榫节点特性试验分析[J].西安建筑科技大学学报(自然科学版),2010(03).
[10]A. Messina, E.J. Williams, T. Contursi. STRUCTURAL DAMAGE DETECTION BY A SENSITIVITY AND STATISTICAL-BASED METHOD[J]. Journal of Sound and Vibration, 1998 (5).
[11]杨智春,党晓娟,谭光辉.基于互相关函数幅值向量和小波变换的复合材料结构损伤检测[J].振动与冲击,2008(11).
