基于小波能量相对熵的HVDC输电线路单端保护方法
2017-03-16李小鹏
李小鹏,高 杉,林 圣,张 纯
(1.国网四川省电力公司电力科学研究院,四川 成都 610072;2.西南交通大学电气工程学院,四川 成都 610031)
Z1=jωL
Z4=Z2‖Z3
‖Z1
x(k)=D1(k)+A1(k)
=D1(k)+D2(k)+A2(k)
M=Mlm+Mml
M>ε
基于小波能量相对熵的HVDC输电线路单端保护方法
李小鹏1,高 杉2,林 圣2,张 纯1
(1.国网四川省电力公司电力科学研究院,四川 成都 610072;2.西南交通大学电气工程学院,四川 成都 610031)
高压直流(high voltage direct current ,HVDC)输电线路目前配置的行波主保护动作速度快,但灵敏性不足,耐过渡电阻能力差,后备保护能够弥补这一缺点,但存在延时时间长的问题。为提高保护的灵敏性和可靠性,研究了基于小波能量相对熵的单端暂态量保护。利用平波电抗器和直流滤波器内外电流特定频带能量的差异,构造单端电流小波能量相对熵判据,实现区内外故障的识别。基于PSCAD/EMTDC的仿真结果表明,该保护原理能快速、可靠地识别区内外故障。
高压直流输电线路;直流滤波环节;小波能量相对熵
0 引 言
HVDC输电线路两端装设的平波电抗器和直流滤波器构成线路边界,对暂态高频信号呈带阻传变特性。文献[1-2]根据直流滤波环节对区内、外故障表现的阻抗特征差异,利用特定频率分量电流实现了全线速动,该方法利用直流线路侧分流器电流,与正常运行时直流线路中很大的负荷电流相比,故障前后的电流变化不明显。因此,文献[3]中利用滤波器支路正常运行时电流很小的特点,仅利用滤波器支路特定频点电流实现了灵敏性较高的全线速动。而针对利用某频段电流幅值大小构建保护判据缺乏普遍适用的整定原则、耐过渡电阻差等问题,又提出了利用高、低频电流幅值之比区分直流线路区内、外故障的方法[4]。为提高保护可靠性,提出了
利用多种不同信号处理方法的直流输电线路暂态量保护,文献[5]提出了一种采用基于小波变换提取暂态信号高频段能量的线路保护方案,而文献[6-8]则分别提出了基于数字滤波器、Hilbert-Huang变换以及改进傅氏算法的直流输电线路保护方案。另外,考虑到特高压直流输电线路也对故障暂态信号高频量有衰减作用,会影响保护对故障的判别,因此提出利用保护元件区分对侧区内、外故障的特高压直流输电线路单端电压暂态保护原理[9]。文献[10-11]利用来自直流线路区外的高频电压信号通过平波电抗器和直流滤波器能量显著减小这一特征,通过计算小波变换后高、低频信号小波能量之比判别区内、外故障。还利用Hilbert-Huang变换求取对侧电流的瞬时频率,以确定故障发生在对侧区内还是区外[12]。
下面拟利用区内、外故障时直流滤波环节两侧电流能谱特征差异,寻找合适的信号处理方法对区内、外故障特征进行量化表达,实现保护的可靠动作。
1 HVDC输电系统结构及故障特征分析
1.1 HVDC输电线路的滤波环节
HVDC输电系统结构包括换流变压器、换流站、平波电抗器、直流滤波器及输电线路。直流线路边界如图1所示,滤波环节由平波电抗器和直流滤波器组成,直流输电系统一般配备双调谐滤波器或三调频滤波器。以某一直流工程为例,分流器1、2分别检测直流滤波环节内、外的电流。随着智能电网的快速发展,使数字化内部数据共享成为可能[3]。
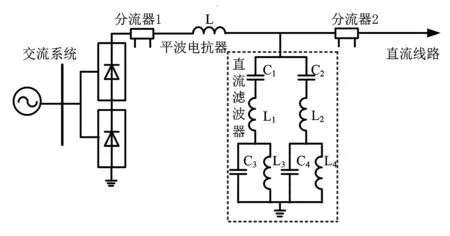
图1 平波电抗器和双调谐滤波器构成的滤波环节
图1中,2组参数不同的直流滤波器构成双调谐滤波器,其中L为平波电抗器参数,C1、C2、C3、C4、L1、L2、L3、L4为直流滤波器参数。设平波电抗器的阻抗为Z1,两直流滤波器的阻抗分别为Z2和Z3,整个直流滤波器组的阻抗为Z4,ω=2πf,则
Z1=jωL
(1)
(2)
(3)
Z4=Z2‖Z3
(4)
由滤波环节结构可知,在直流输电线路区内故障和区外故障时,滤波环节对于电流的阻滞作用也不同。也就是说,滤波环节内、外电流的各频段能量差异明显,利用该特征的输电线路保护能够实现全线速动。
1.2 直流工程滤波环节的阻抗特征分析
HVDC单极输电线路滤波环节如图2所示。区外故障时,高频分量受到较强的阻滞作用,两分流器处感受到的电流高频分量较小。线路区内发生故障时,故障产生的高频分量无阻碍地传到分流器2处;而分流器1处的电流将受到滤波环节的影响高频成分衰减严重,因此直流输电线路滤波环节的存在使两侧电流各频段能量不同。
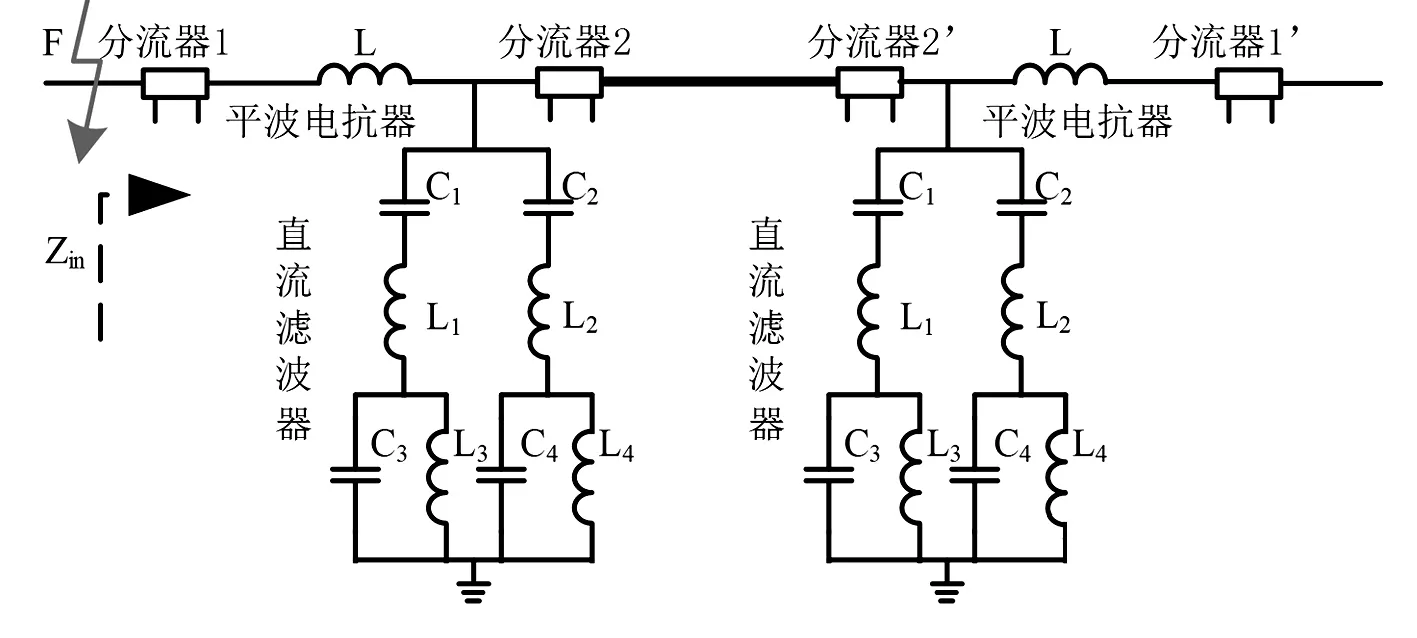
图2 HVDC单极输电线路滤波环节示意图
图2给出了从阀侧看直流滤波环节的网络拓扑,忽略直流线路阻抗,且令线路对端平波电抗器短路。当平波电抗器外侧发生故障时,从故障点看进去的输入阻抗为

(5)
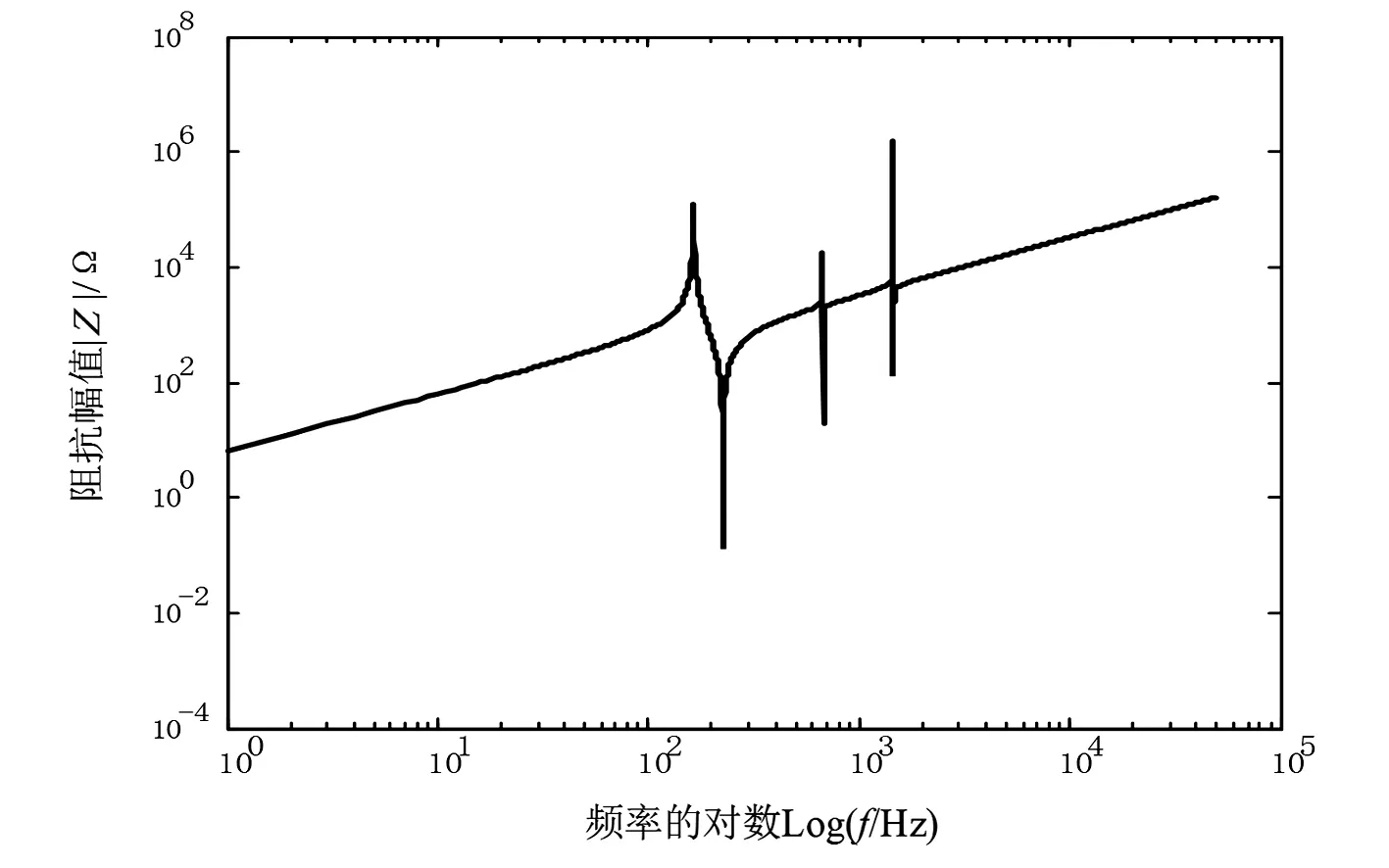
图3 滤波环节阻抗特性
对应于图2所示发生区外故障时的阻抗特征如图3所示。其对高频成分有明显的阻滞作用,频率越高,阻滞作用越明显,即频率较高的分量难以从直流线路区外传到直流线路上。而低频部分则不受影响,因此直流输电系统发生区外故障时,电流通过滤波环节高频段能量衰减,低频段能量变化不大。
2 小波能量相对熵
2.1 小波变换的基本原理
对信号x(k)进行小波变换后,在第j分解尺度下k时刻的高频分量系数为dj(k),低频分量系数为aj(k),进行单支重构后得到的信号分量Dj(k)、Aj(k)所包含的信息频带范围如下:
(6)
式中,fs为信号采样频率。则原始信号序列x(k)可以表示为各分量的和,即
x(k)=D1(k)+A1(k)
=D1(k)+D2(k)+A2(k)
(7)
为统一,用DJ+1(k)代替AJ(k)则有
(8)
式中,Dj(k)为信号x(k)在不同尺度下的分量,也称为信号的多尺度表示。此多尺度表示可以直接用作分类的特征子集。
2.2 小波能量相对熵的定义

(9)
式中,i=1,2,…,h,共有h个信号,由此可得尺度j下信号xi(k)的能量与总能量之比为
(10)
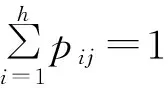
由此可得,h=2时,两信号xl(k)、xm(k)在尺度j下的能量与总能量之比分别为pij、pmj。定义信号xl(k)相对于信号xm(k)的小波能量相对熵为
(11)
类似的,信号xm(k)相对于信号xl(m)的小波能量相对熵为Mml。因此,定义信号xm(k)与信号xl(k)之间的小波能量相对熵为
M=Mlm+Mml
(12)
利用小波能量相对熵描述滤波环节内外检测到的电流的各频段能量差异,随时间的变化。
2.3 区内外故障时小波能量相对熵特征
某实际工程仿真模型中,在正极线路区内1 499 km处设置金属性接地故障,故障时刻为0.35 s。图4中电流是两极电流经相模变换解耦后的电流,由图可知,直流滤波环节内外电流小波能量相对熵大于1。
在逆变站负极平波电抗器外侧设置过渡电阻为300 Ω的接地故障,故障时刻为0.35 s。如图5直流滤波环节内外电流小波能量相对熵小于1。
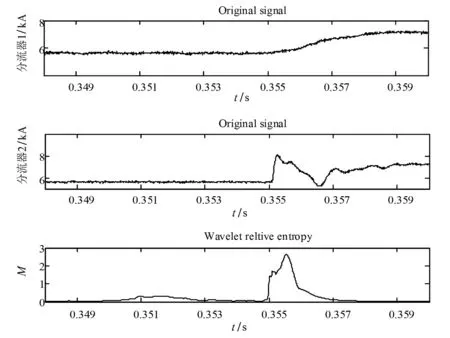
图4 线路末端故障时两解耦后电流波形及小波能量相对熵
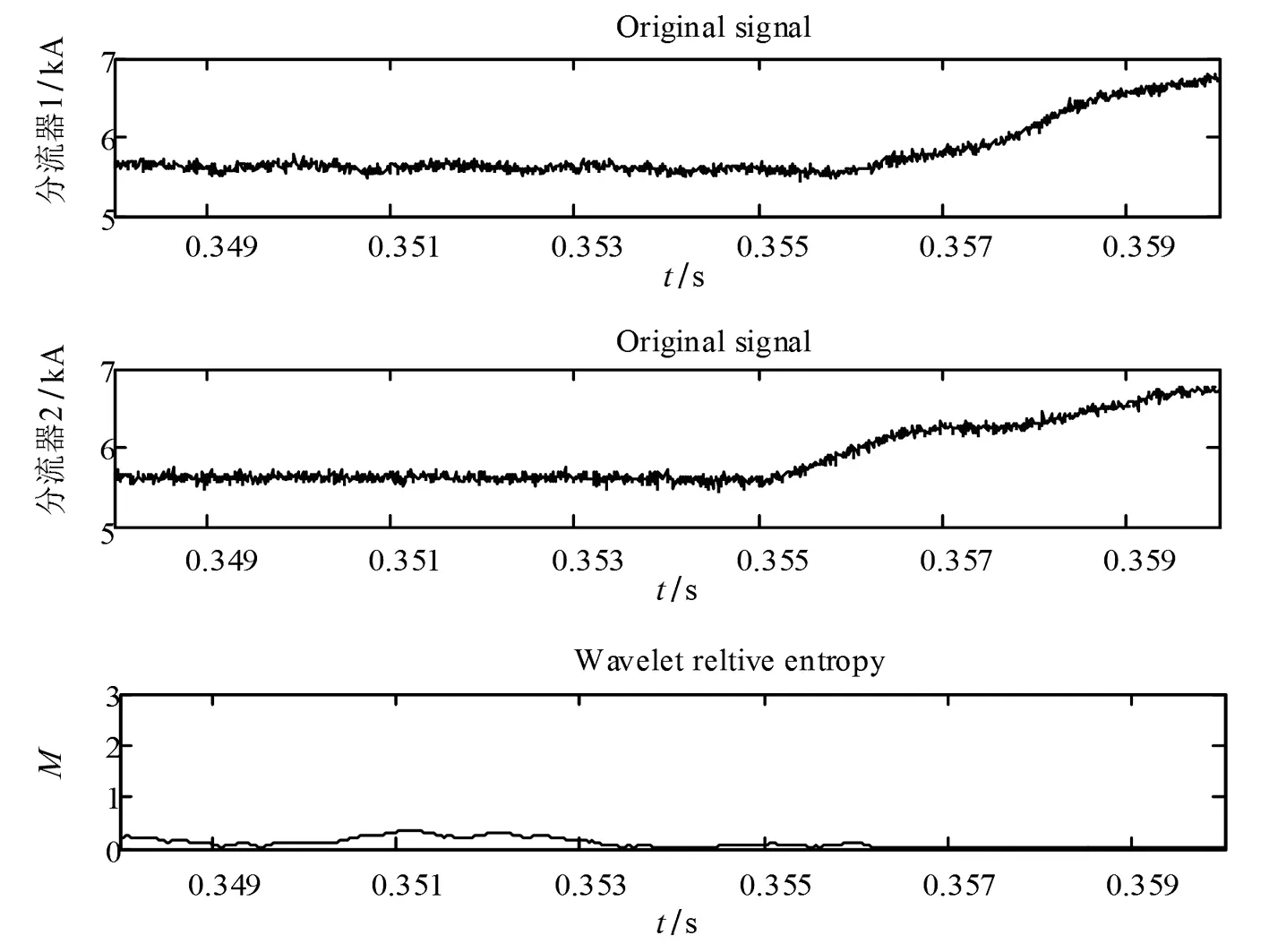
图5 逆变侧电抗器外故障时两解耦后电流波形及小波能量相对熵
3 基于小波能量相对熵的HVDC 输电线路单端保护
小波能量相对熵可以表征两信号能谱值的概率分布之间的差别,相对熵值越大,信号间差别越大。并且小波变换后对不同频带信息的选取,可以使小波能量相对熵表征HVDC输电系统滤波环节两侧电流信号间特定频段的差别。由所提分析可知,当发生区内故障时,滤波环节两侧电流信号差别较大,相对熵值较大;当发生区外故障时,滤波器两侧电流信号差别较小,相对熵值较小。因此,利用故障后直流滤波环节两侧电流信号的小波能量相对熵可实现区内故障的识别。由式(13)计算两个分流器感受到的电流信号的小波能量相对熵,即M表示两电流信号的小波能量相对熵,ε为给定阈值,若
M>ε
(13)
则判断为HVDC输电线路区内故障。
小波分解、重构层数选取4,可区分受阻滞作用较明显的高频段与不明显的低频段。数据窗长度选为3 ms。
综上,利用小波能量相对熵识别区内、外故障的流程如图6所示。

图6 基于小波能量相对熵的HVDC输电线路单端保护流程图
4 仿真分析
在PSCAD/EMTDC中建立±800 kV直流输电系统仿真模型。模型参数设置参考文献[13],系统额定电压为800 kV,额定电流为4 kA,双极输电容量为6 400 MW,直流线路全长l为1 500 km。模型中平波电抗器为500 mH,直流滤波器采用双调谐滤波器。仿真设置采样频率为100 kHz,加入了信噪比为40 dB的高斯白噪声,数据窗选用3 ms,ε确定为1。
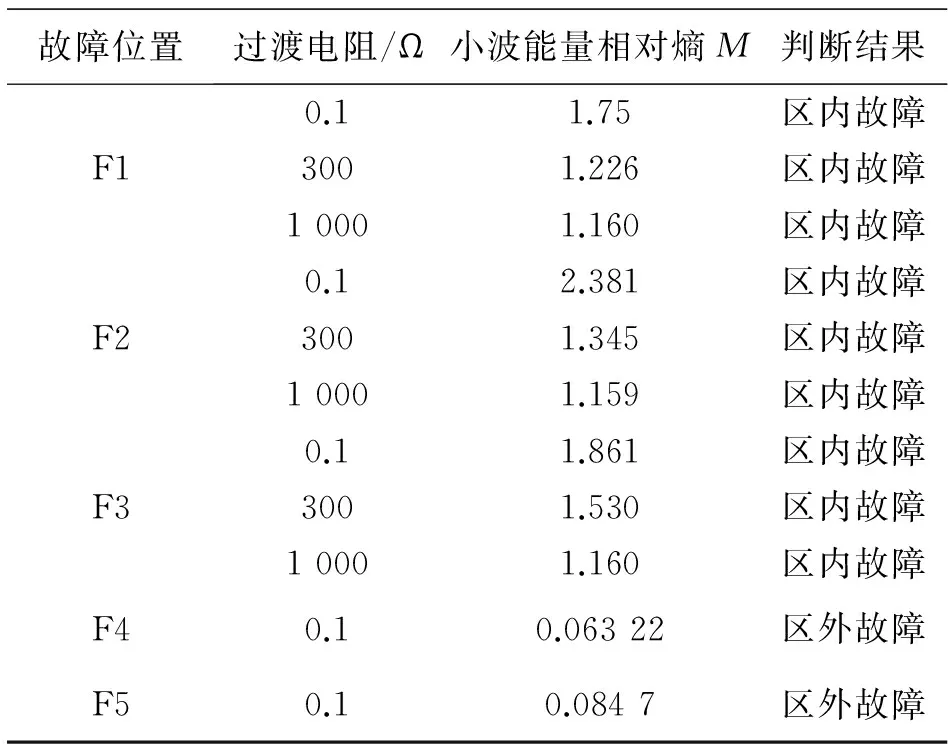
表1 不同故障工况下单端保护判断结果
为考察所提出的保护原理在不同故障工况下的适应性,HVDC输电系统仿真中,设置如下故障:正极线路区内故障F1(故障距离为100 km),负极线路区内故障F2(故障距离为750 km),极间故障F3(故障距离为500 km),正极整流站平波电抗器外侧故障F4,逆变侧交流母线故障F5。表1为在不同故障位置、故障距离及故障过渡电阻下的保护判断结果。
由表1的结果可知,所提出的保护原理不受故障位置影响,可正确判别线路末端故障,耐故障过渡电阻能力强,具有一定的耐噪声能力,在不同故障工况下均有较好的适应性。
5 结 论
在分析高压直流输电线路区内外故障时线直流滤波环节的阻抗特征的基础上,利用小波能量相对熵实现了高压直流线路单端保护。保护仅利用故障后3 ms电流数据快速识别区内外故障,无需线路对端的电气量信息。通过理论分析和仿真分析得到以下结论:
1) 小波能量相对熵可定量评价信号或系统状态的不确定性程度。通过小波能量相对熵可准确描述滤波环节两侧电流信号的能谱差异。
2) 区外故障时,直流滤波环节两侧分流器检测到的电流小波能量相对熵很小;直流滤波环节两侧分流器检测到的电流小波能量相对熵较大,据此可以区分区内外故障。
3) 大量PSCAD/EMTDC仿真结果表明,该保护方案在各工况下都能快速、可靠地识别区内外故障。
[1] 高淑萍,索南加乐,宋国兵,等.利用单端电流的高压直流输电线路全线速动保护[J].中国电机工程学报,2012,32(7):107-113.
[2] 宋国兵,高淑萍,索南加乐,等.一种识别高压直流输电线路区内、外故障的单端电气量全线速动保护方法:中国,201110209681.9[P].2011-11-23.http://www.drugfuture.com/cnpat/cn_patent.asp.
[3] 宋国兵,褚旭,高淑萍,等.利用滤波器支路电流的高压直流输电线路全线速动保护[J].中国电机工程学报,2013,33(22):120-126.
[4] 宋国兵,冉孟兵,褚旭,等.利用高低频电流幅值比的VSC-HVDC 输电线路全线速动保护新原理[J].电网技术,2014,38(5):1402-1407.
[5] You M,Zhang B H,Cao R F.Study of Non-unit Transient-based Protection for HVDC Transmission Lines[C].Asia-Pacific Power and Energy Engineering Conference,Wuhan,China:Wuhan University,2009:1-5.
[6] 张嵩,尤敏,张保会,等.基于数字滤波方法的单端暂态量保护边界元件的实现[C].中国高等学校电力系统及其自动化专业第二十五届学术年会,长沙,中国:长沙理工大学,2009:1-6.
[7] Zhang S,Zhang B H,You M.Realization of the Transient-based Boundary Protection for HVDC Transmission Lines[C].International Conference on Power System Technology,Hangzhou,China:CSEE,2010:1-7.
[8] 张保会,张嵩,尤敏,等.高压直流线路单端暂态量保护研究[J].电力系统保护与控制,2010,38(15):18-23.
[9] 陈仕龙,束洪春,万春红,等.一种特高压直流输电线路单端电压暂态保护原理[J].电力系统保护与控制,2013,41(3):26-31.
[10] 束洪春, 刘可真, 朱盛强, 等. ±800 kV特高压直流输电线路单端电气量暂态保护[J].中国电机工程学报, 2010, 30(31): 108-117.
[11] 刘可真.特高压直流输电线路暂态保护和故障测距问题研究[D].哈尔滨:哈尔滨工业大学,2013.
[12] 张杰.特高压直流输电线路暂态保护研究[D].昆明:昆明理工大学,2014.
[13] 赵婉君.高压直流输电工程技术[M].北京:中国电力出版社,2004.
The presented main protection for HVDC transmission lines acts fast, but it has low sensitivity and low anti-resistance ability. The backup protection can compensate this disadvantage but its operation speed is slow. In order to improve the reliability and sensitivity of the protection, the single-ended transient protection based on relative entropy of wavelet energy is studied. The internal fault and external fault are discriminated by the relative entropy criterion which is constructed using the differences of the currents on both sides of the smoothing reactor and the DC filter under the specific frequency bands. Simulation result based on PSCAD/EMTDC show that the proposed protection scheme can discriminate the internal fault and external fault quickly and reliably.
HVDC transmission line; DC filtering unit; relative entropy of wavelet energy
中国博士后科学基金资助项目(2016M592659)
TM773
A
1003-6954(2017)01-0071-05
2016-09-21)
