基于支路能量时空特征的电力系统暂态稳定性分析
2017-03-16刘挺坚胥威汀刘友波许立雄
刘挺坚, 苟 竞, 胥威汀, 刘友波, 许立雄
(1. 四川大学电气信息学院, 四川 成都 610065;2. 国网四川省电力公司经济技术研究院, 四川 成都 610041)
ηl-k=El-k/El
S1=El/Hl
Xm(i)={u(i),u(i+1), …, u(i+m-1)}
ρApEn(m,r,N)=φm(r)-φm+1(r)
基于支路能量时空特征的电力系统暂态稳定性分析
刘挺坚1, 苟 竞2, 胥威汀2, 刘友波1, 许立雄1
(1. 四川大学电气信息学院, 四川 成都 610065;2. 国网四川省电力公司经济技术研究院, 四川 成都 610041)
提出支路能量分布熵和支路能量近似熵指标,分别从扰动能量在电网中的空间分布聚集程度和从扰动能量随时间推移的振荡态势来分析故障后电力系统的暂态稳定性。首先简述系统动态模型和基于结构保留模型的支路势能分析方法,引入复杂系统熵理论构造支路能量分布熵指标;同时引入近似熵与多尺度熵理论构造支路能量近似熵指标,进一步给出基于两类熵指标的暂态稳定分析方法。四川电网算例研究验证了:线路故障注入电网的扰动能量越大,支路能量分布熵越小,则关键支路割集所聚集的能量越大,系统越容易失稳;支路能量近似熵越小,则聚集在支路上的能量随时间推移越发增加,系统越容易失稳。
暂态稳定性;支路势能法;空间分布熵;近似熵
0 引 言
近年来,大停电事故在全球范围内时有发生,对社会稳定和经济发展造成了极大的损害[1-3],引起了电力系统运行人员和科研人员对安全稳定分析工作的广泛关注。
20世纪50年代,能量函数方法[4]被引入到电力系统的暂态稳定分析中,由此展开了电力系统能量函数分析方法的研究。文献[5]基于多机电力系统的经典模型,采用首次积分法构造了暂态能量函数,实现了同步稳定性的定量评估。文献[6]首次提出了基于结构保留模型的暂态能量函数,消除了经典模型不能计及转移电导以及负荷无功电压动态响应等问题。文献[7]提出了单机能量函数,验证
了系统失去同步稳定性仅由部分机组的失稳能量决定。文献[8]则提出了扩展等面积方法(extended equal area criterion,EEAC),用角度中心的概念将多机系统等值为两机系统进而等值为单机无穷大系统,从而可采用等面积定则来衡量多机系统的稳定性。
经过几十年的发展与改进,能量函数方法得到了更广泛的应用。文献[9-10]提出了静态势能函数,其中静态支路势能函数可从支路传输能力的角度定量评估电网脆弱性,而静态节点势能函数可统一量化负荷节点在系统不同无功注入成分影响下的电压脆弱性。基于复杂网络理论介数的概念,文献[11]建立了计及暂态动能注入介数和支路势能信息的支路暂态脆弱性指标,实现了大扰动下脆弱输电线路的快速预判。文献[12]推导了基于发电机机端电气状态量的相对能量函数,通过两阶段聚类分群实现了系统临界机群的快速辨识。文献[13]将诸多电气状态参数统一到能量函数框架下,以能量转移分布熵和单位转移能量密度提取系统连锁故障演变趋势,辨识连锁开断薄弱元件。
下面提出支路能量分布熵和支路能量近似熵指标,分别从扰动能量在电网中的空间分布聚集程度和从扰动能量随时间推移的振荡态势来分析故障后电力系统的暂态稳定性。首先简述系统动态模型和基于结构保留模型的支路势能分析方法,引入复杂系统熵理论构造支路能量分布熵指标,引入近似熵与多尺度熵理论构造支路能量近似熵指标,进一步给出基于两类熵指标的暂态稳定分析方法。最后以四川电网作为对象进行算例分析验证所提方法的有效性。
1 电力系统动态模型与支路能量函数
1.1 系统动态模型
设电力系统有nG个发电机节点,nB个母线节点和nL条支路(包括输电线路和变压器)。惯性中心(center of inertia, COI)参考系下系统动态模型为
(1)
式中:Mi为发电机i的惯性系数;MT为系统惯性系数,是各发电机惯性系数之和;ωi和δi分别为发电机i相对于惯性中心的转速与转角;Pmi和Pei分别为发电机i的输入机械功率和输出电磁功率;PCOI为惯性中心的加速功率。
若发电机采用经典模型,负荷采用恒阻抗模型,并采用计及发电机暂态电抗的增广网络,那么Pei和PCOI满足:
(2)
(3)
式中:Ei和Ej分别为发电机i和发电机j的内电势;Gij和Bij分别为收缩到发电机内节点的网络电导与电纳。
1.2 支路势能函数
基于结构保留模型的能量函数理论,根据势能函数的积分原理,电网各支路势能可表示为
(4)
考虑支路功率传输关系:

(5)
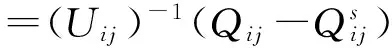
(6)
将式(5)和式(6)代入式(4)中即可得到支路势能为
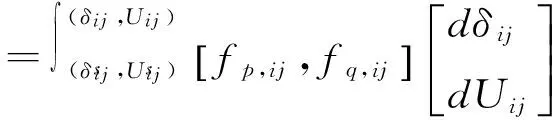
式中:Eij为节点i、j之间的支路势能;δi、δj分别为节点i、j的相角,且有δij=δi-δj;Ui、Uj分别为为节点i、j的电压幅值,且有Uij=Ui-Uj;Pij、Qij分别为节点i、j之间的当前有功、无功传输量;Gij、Bij分别为节点i、j之间的支路电导和支路电纳;Uis、Ujs、δis、δjs、Pijs、Qijs分别表示对应变量的初始稳态值。
取初始稳态作为势能的参考点,支路势能表达了线路潮流、节点电压在故障后暂态阶段相对于初始稳态的瞬时偏移效应,其动态轨迹反映了系统暂态稳定态势。
2 基于支路能量空间分布特征的暂态稳定性分析
2.1 复杂系统熵理论
熵(entropy)是热力学系统的一种状态函数,是对系统紊乱程度的一种度量。其后香农又提出信息熵,一般用来衡量离散系统的信息不确定度,表征系统的有序/无序程度。当系统的n种状态等概率出现时,系统有序程度最低,信息熵最大;当系统处于唯一状态时,系统的有序程度最高,信息熵最小。
电力系统作为一个复杂自组织能量平衡系统,系统内部的稳定平衡可以通过系统内部能量分布的熵变过程来描述,因此可定义电力系统能量熵H为
(8)
式中:ηi=Ei/E为元件i的能量分布率;N为系统元件总数。
2.2 基于支路能量分布熵的暂态稳定分析方法
若线路l发生故障扰动,故障将对电网注入扰动能量。扰动能量以支路势能的形式分布和储存在电网各支路中。支路能量空间分布的聚集程度反映了电网各支路对扰动能量的分摊消纳情况,若支路能量集中分布在少数线路上,将可能因为这些支路无法消纳扰动能量而造成系统从这些支路所构成的关键割集撕裂,最终导致电力系统失去同步稳定性。
由于暂态支路能量具有时变性,不能仅从某一时间断面来评价扰动能量在电网中的聚集程度,因此需从暂态过程中支路能量的累积效应来研究能量分布。设线路l发生故障后,线路k在暂态过程中所承受的累计能量效应El-k为
(9)
式中:Ek(t)为线路k在故障后暂态过程中的瞬时支路势能值;tcl为故障清除时刻;ts为故障后系统到达稳定平衡状态的时刻。一般来说,ts为无穷大时刻,实际应用中时间取无穷大则不利于计算,这里对ts取时域仿真时间。
因此线路l发生故障对电网各支路的总体扰动能量冲击El为
(10)
线路k所承担线路l故障对电网总体扰动能量冲击的比例用线路k的能量冲击率ηl-k来表示。
ηl-k=El-k/El
(11)
定义线路l故障扰动下系统的支路能量分布熵为
(12)
在线路l故障扰动给系统注入的扰动能量El一定的情况下,Hl的大小反映了扰动能量在电网各支路中的空间分布特性。Hl越小表示扰动能量越集中分布在少数几条支路上,系统将面临更大的失稳风险;反之,Hl越大表示扰动能量越均匀分摊到电网各支路上,系统相对安全稳定。
进一步定义线路l故障扰动下系统暂态稳定性指标S1为
S1=El/Hl
(13)
El越大,线路l故障扰动对系统的能量冲击越大,Hl越小,线路l故障注入的扰动能量在电网中越聚集,则线路l故障扰动下系统暂态稳定性指标S1越大,那么线路l故障扰动越容易导致系统失稳。
3 基于支路能量时间演变特征的暂态稳定性分析
3.1 近似熵与多尺度熵
近似熵[14](approximate entropy)表示前一数据序列对后一数据序列的可预测性,反映了时间序列上的复杂度,可用于研究非线性动力学系统的变化规律。
对于一个长度为N的原始时间序列X={u(i),u(i+1), …,u(N)},对重构为m维矢量:
Xm(i)={u(i),u(i+1), …,u(i+m-1)}
(14)
其中,i=1,2,…,N-m+1。
对每一个标量i,计算矢量X(i)与所有矢量X(j)(j=1,2,…,N-m+1)矢量之间的距离为
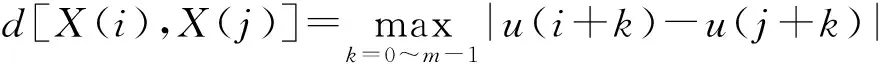
(15)
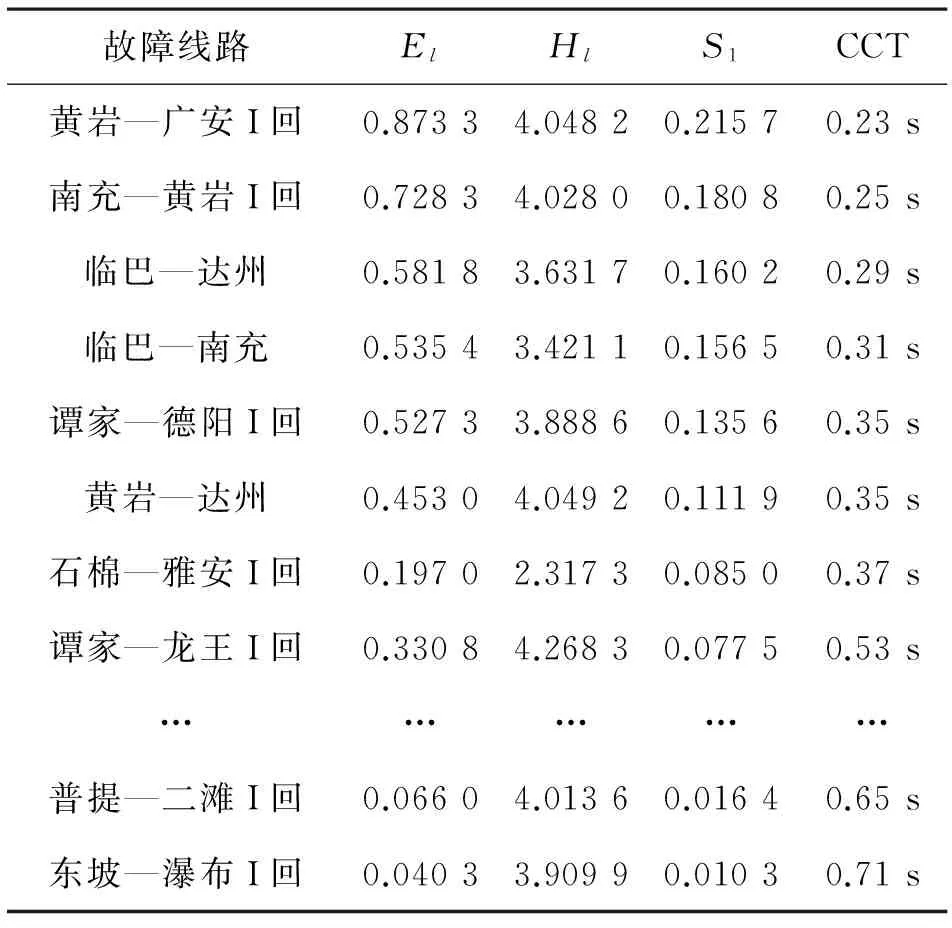
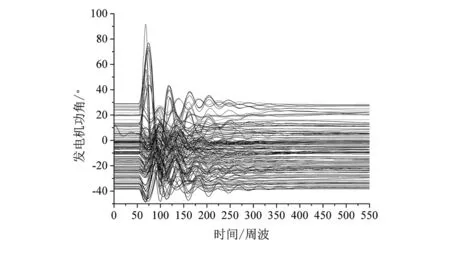
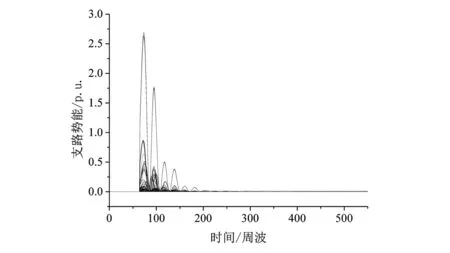
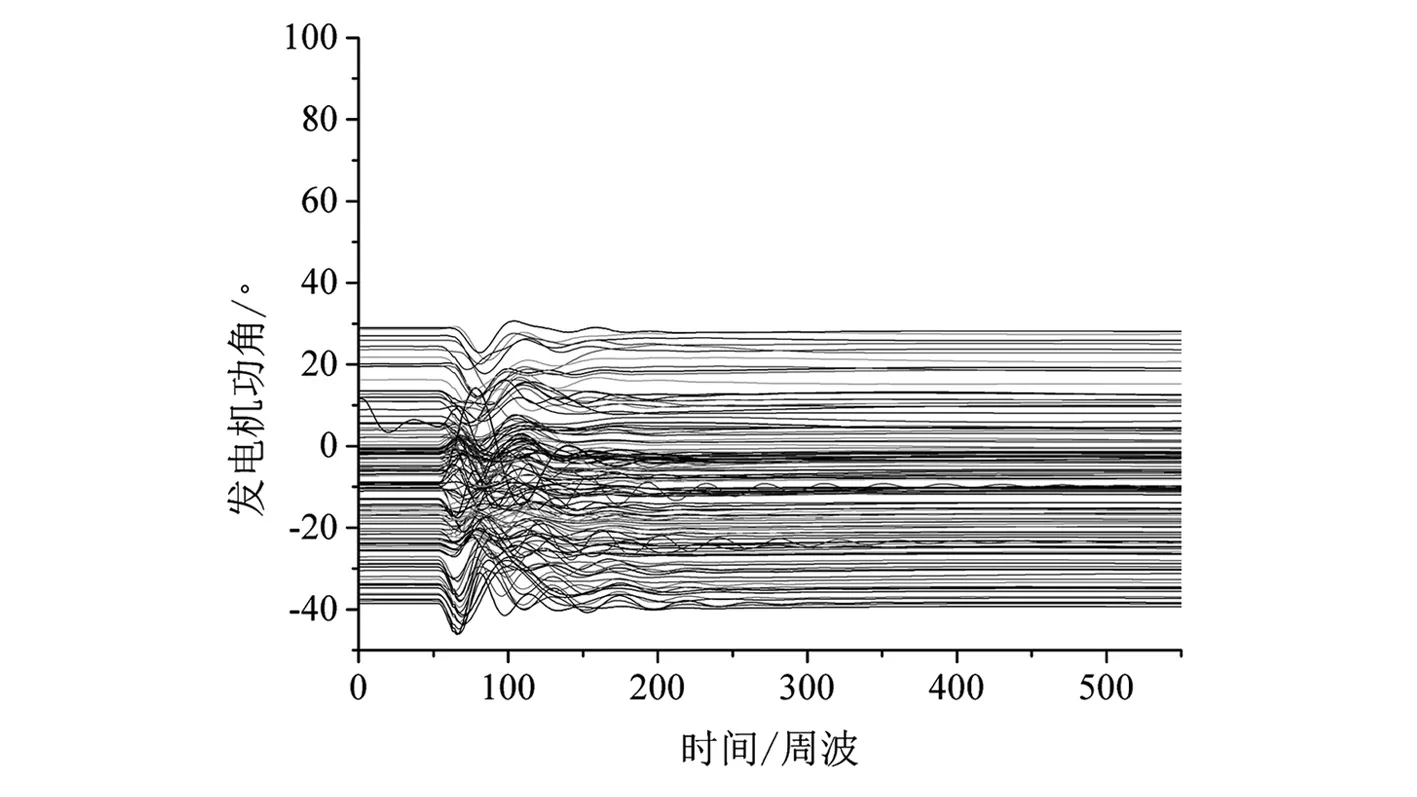
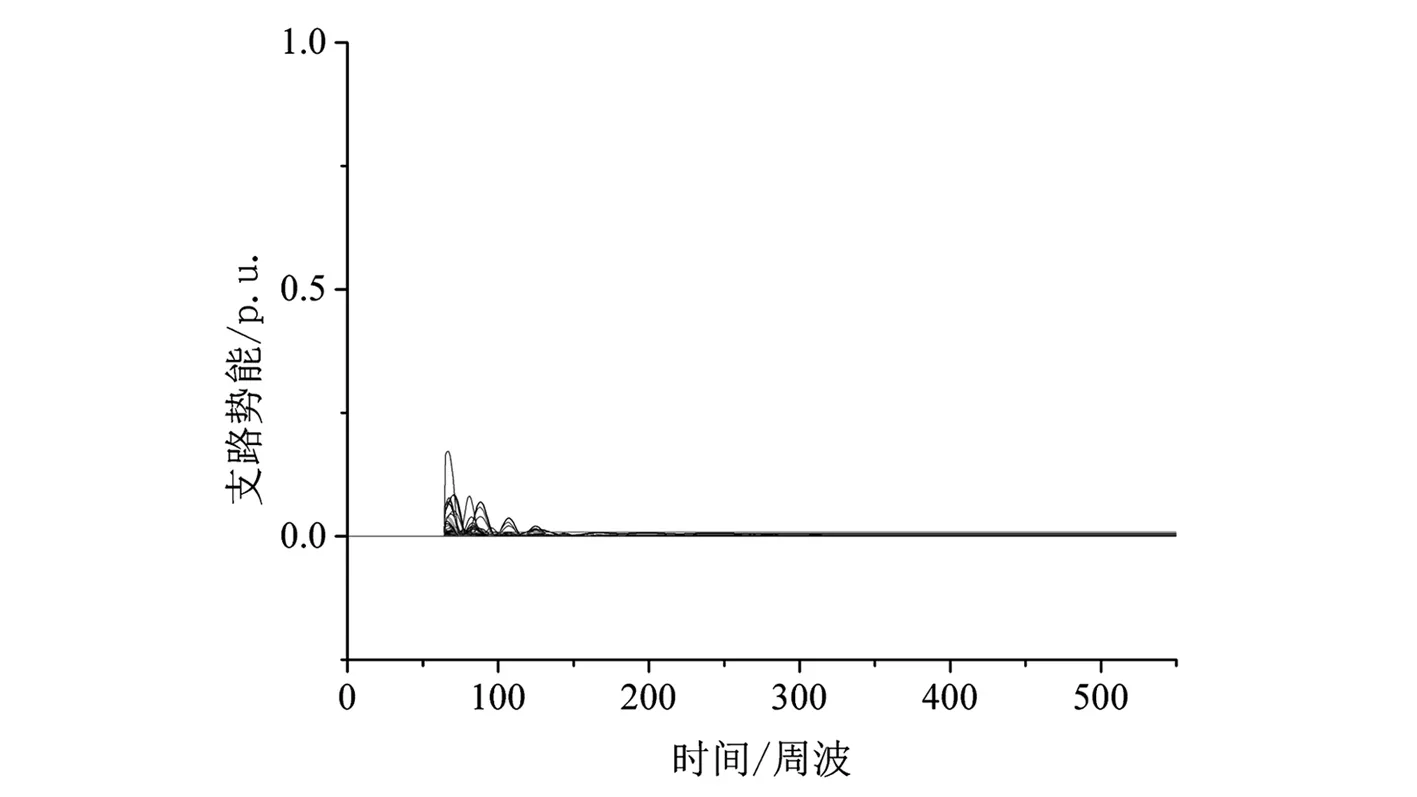
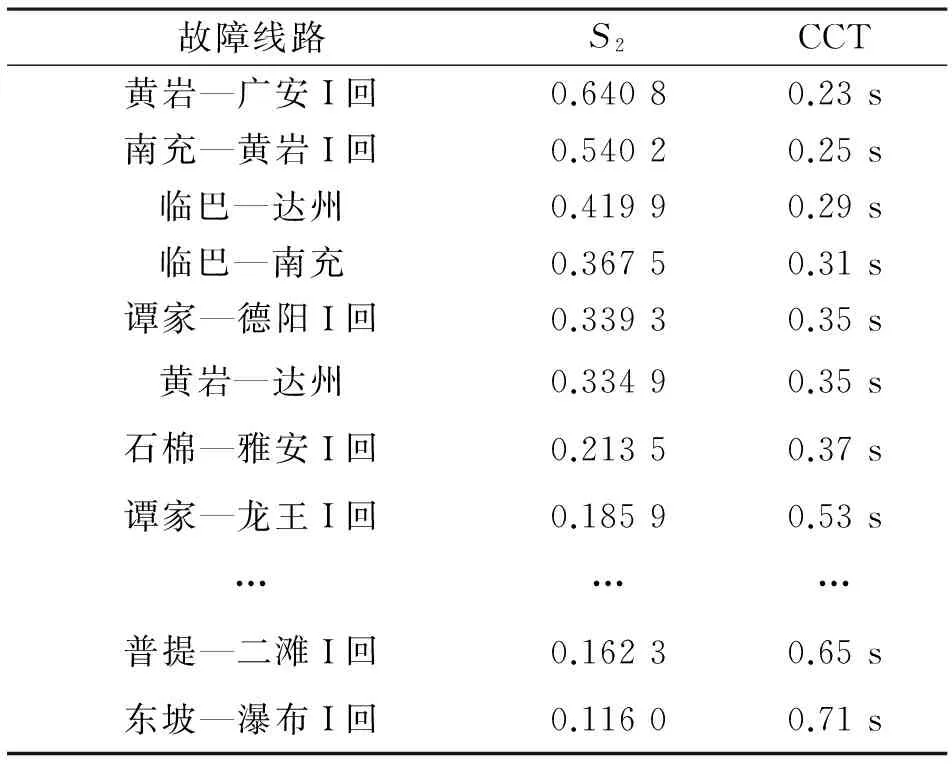
设容限r>0,统计d[X(i),X(j)] (16) 式中,j=1,2,…,N-m+1。 对Cim(r)取对数再求和,然后求其对所有i的平均值φm(r)为 (17) 将矢量维数增加1变为m+1,重复上述过程计算φm+1(r),则此时间序列的近似熵可表示为 (18) 实际计算中时间序列的长度不可能为无限,因此对有限序列N,采用式(19)来计算近似熵的估计值: ρApEn(m,r,N)=φm(r)-φm+1(r) (19) 多尺度熵(multi-scale entropy)首先对原始时间序列作粗粒化变换,设尺度变换因子为τ,则原始时间序列粗粒化后为 (20) 式中:新时间序列长度为N/τ,当尺度因子为1时,即为原始时间序列;当尺度因子不为1时,粗粒化为新时间序列yjτ。对于粗粒化后的时间序列,计算其近似熵,由此得到原始时间序列在给定时间尺度下的近似熵值,即反映的是原始时间序列在给定时间尺度上的复杂度。容限r的取值一般与原始时间序列的标准差相关(一般取r=0.1~0.25 SD,SD为原始时间序列标准差);对于参数m,研究表明当取维数m=2时计算结果的准确性对序列长度N的依赖性最小。 3.2 基于支路能量近似熵的暂态稳定分析方法 故障清除后,若支路能量随时间推移而衰减,即电网中各支路能够消纳故障注入的扰动能量,那么随时间推移系统进入故障后稳定平衡状态;若部分支路的支路能量随时间推移而增长,即该部分支路没有能力消纳故障注入的扰动能量,那么系统将从该部分支路组成的割集处失稳解列。因此可从支路能量的时间演化特征来分析电力系统的暂态稳定性。 给定尺度因子τ,对各支路的势能轨迹进行尺度为τ的粗粒化变换得到新轨迹序列,对新轨迹序列分析其近似熵,取各支路近似熵值的最大值作为系统的暂态稳定性指标S2: (21) 以PSD-BPA的时域仿真程序作为仿真计算工具,采用四川电网某枯大运行方式作为算例对象,验证所提分析方法的有效性。 4.1 基于支路能量分布熵的暂态稳定性分析 考虑将四川电网所有500 kV输电线路作为三相短路故障的故障元件,故障清除时间取10个周波,采用PSD-BPA进行时域仿真计算得到系统的故障响应,采用基于支路能量分布熵的暂态稳定分析方法来进行暂态稳定性评估,计算结果如表1所示。 在算例运行方式中,川东北区域的临巴电厂和广安厂机组的出力水平较高,因此东北区域线路故障的临界切除时间(critical clearance time,CCT)较短,线路故障对系统的扰动水平也较高;而金沙江流域、大渡河流域水电厂机组的出力水平相对较低:因此相应区域线路故障的临界切除时间较高,线路故障对系统的扰动水平也较低。基于广义支路能量分布熵的暂态稳定分析方法与线路故障场景的临界切除时间也基本相符,因此验证了该方法的有效性。 表1 基于支路能量分布熵的暂态稳定性分析 图1和图2分别给出“黄岩—广安I回”输电线路发生三相短路故障后发电机功角响应轨迹和支路势能响应轨迹,图3和图4则分别给出“普提—二滩I回” 输电线路发生三相短路故障后发电机功角响应轨迹和支路势能响应轨迹。从发电机功角轨迹和支路势能轨迹的振荡幅度可以看出“黄岩—广安I回”故障对系统的扰动冲击更大,故障后系统的稳定裕度更低。 图1 “黄岩—广安I回”三相短路故障下发电机功角响应轨迹 4.2 基于支路能量近似熵的暂态稳定分析方法 取尺度变换因子τ=10,采用4.1节所产生的故障样本来验证基于支路能量近似熵的暂态稳定分析方法的有效性,计算结果如表2所示。 图2 “黄岩—广安I回”三相短路故障下支路势能响应轨迹 图3 “普提—二滩I回”三相短路故障下发电机功角响应轨迹 图4 “普提—二滩I回”三相短路故障下支路势能响应轨迹 故障线路S2CCT黄岩—广安I回0.64080.23s南充—黄岩I回0.54020.25s临巴—达州0.41990.29s临巴—南充0.36750.31s谭家—德阳I回0.33930.35s黄岩—达州0.33490.35s石棉—雅安I回0.21350.37s谭家—龙王I回0.18590.53s………普提—二滩I回0.16230.65s东坡—瀑布I回0.11600.71s 由表2可知,基于支路能量近似熵的暂态稳定性指标S2基本上随故障临界切除时间增加而减少,从定性上验证了稳定性指标S2可用于暂态稳定分析。 结合支路势能函数与复杂系统分布熵和近似熵理论,提出了一种基于支路能量时空特征的电力系统暂态稳定分析方法。首先从支路能量在空间分布的特征出发,采用复杂系统熵理论对故障注入扰动能量在电网中分布聚集程度进行评估,构造扰动能量冲击指标来分析系统暂态稳定性;然后从支路能量随时间推移的特征出发,采用复杂系统近似熵理论对支路能量在暂态过程中振荡演化态势进行分析,利用近似熵值有效识别暂态脆弱线路以及评估系统暂态稳定性。四川电网算例验证了:线路故障注入电网的扰动能量越大,支路能量分布熵越小,则关键支路割集所聚集的能量越大,系统越容易失稳;支路能量近似熵越小,则聚集在支路上的能量随时间推移越发增加,系统越容易失稳。所提基于支路能量时空特征的暂态稳定分析方法从扰动能量在系统中分布、传播和消纳的角度分析电网稳定性变化趋势,算例结果与故障场景的临界切除时间基本相符,为特大型电力系统暂态稳定分析提供了新思路。 [1] U.S.-Canada Power System Outage Task Force. Final Report on the August 14, 2003 Blackout in the United States and Canada: Causes and Recommendations.[R/OL]http://energy.gov/sites/prod/files/oeprod/DocumentsandMedia/BlackoutFinal-Web.pdf. [2] Final Report of the Investigation Committee on the 28 September 2003 Blackout in Italy.[R/OL]http://www.rae.gr/old/cases/C13/italy/UCTE_rept.pdf. [3] Final report system Disturbance on 4 November 2006.[R/OL]https://www.entsoe.eu/fileadmin/user_upload/_library/publications/ce/otherreports/Final-Report-20070130.pdf. [4] 刘笙,汪静.电力系统暂态稳定的能量函数分析[M].上海:上海交通大学出版社,1996.[5] T. Athay, R. Podmore, S. Virmani. A Practical Method for the Direct Analysis of Transient Stability [J]. IEEE Trans. on Power Apparatus and Systems, 1979, 36(11): 1423-1429. [6] A.R. Bergen, D.J. Hill. A Structure Preserving Method for Power System Stability Analysis [J]. IEEE Trans. on Power Apparatus and Systems, 1981, 100(1): 25-35. [7] A.N. Micheal, A.A. Fouad, V. Vittal. Power System Transient Stability Using Individual Machine Energy Functions [J]. IEEE Trans. on Circuits and Systems, 1983, CAS-30(5): 266-276. [8] Y. Xue, T. Van Cutsem, M. R. Ribbens-Pavella. A Simple Direct Method for Fast Transient Stability Assessment of Large Power Systems [J]. IEEE Trans. on Power Systems, 1988, 3(2): 400-412. [9] 刘群英, 刘俊勇, 刘起方. 基于支路势能信息的电网脆弱性评估[J]. 电力系统自动化, 2008, 32(10): 6-11. [10] 刘群英, 刘俊勇, 刘起方. 节点势能架构下的电压脆弱性评估[J]. 中国电机工程学报, 2008, 28(25): 30-37. [11] 刘友波, 刘俊勇, 王民昆, 等. 计及动能注入介数的线路暂态脆弱性快速评估[J]. 中国电机工程学报, 2011, 31(13): 40-47. [12] 苟竞, 刘俊勇, 魏震波, 等. 一种基于发电机对相对能量的电力系统临界机群快速辨识方法[J]. 中国电机工程学报, 2015, 35(24):6322-6330. [13] 苟竞, 刘俊勇, 刘友波, 等. 基于能量熵测度的电力系统连锁故障风险辨识[J]. 电网技术, 2013, 37(10): 2754-2761. [14] S.M. Pincus. Approximate Entropy as A Measure of System Complexity[J]. Proceedings of the National Academy of Sciences of the United States of America, 1991, 88(6): 2297-2301. Two performance indexes, that is, distribution entropy and approximation entropy of power system branch potential energy, are proposed for transient stability assessment. The general dynamic model of power systems and branch potential energy is firstly introduced. Distribution entropy is used to describe the spatial feature of branch potential energy and approximate entropy is used to describe the temporal feature of branch potential energy. After that, the methods for transient stability based on the proposed two performance indexes are presented in detail. Case study on the transmission system of Sichuan province demonstrates that, a higher energy injection caused by a fault and smaller energy distribution entropy will result in a more unstable system. Numerical results also show that smaller energy approximate entropy indicates that potential energy will accumulate faster in the critical subset of transmission lines, thus the system will be more unstable. transient stability; branch potential energy; spatial distribution entropy; approximate entropy 国家自然科学基金重点项目(51437003) TM712 A 1003-6954(2017)01-0009-05 2016-11-02)4 算例分析
5 结 论
