射影平坦且具有相对迷向平均Landsberg曲率的(α,β)-度量
2017-03-16程新跃刘树华
程新跃,刘树华
(重庆理工大学 理学院, 重庆 400054)
射影平坦且具有相对迷向平均Landsberg曲率的(α,β)-度量
程新跃,刘树华
(重庆理工大学 理学院, 重庆 400054)

射影平坦芬斯勒度量;(α,β)-度量;Landsberg曲率;平均Landsberg曲率
1900年,数学家希尔伯特提出了23个著名的数学问题。其中的第4个问题是:刻画定义在Rn的一个开子集上的度量函数,使得直线是关于这个度量的测地线。希尔伯特第四问题在正则情形下就是刻画以直线为测地线的芬斯勒度量。将希尔伯特第四问题在正则情形下的光滑解称为射影平坦的芬斯勒度量。
y∈TxBn≅Rn
(1)
因此,在黎曼几何中,希尔伯特第四问题已经被完全解决。但在芬斯勒几何中,这一问题还远未被解决。
由大量的研究经验可知:射影平坦芬斯勒度量的刻画与度量的曲率性质密切相关。
1929年,L.Berwald证明了射影平坦的芬斯勒度量具有标量旗曲率[1]。2003年,沈忠民教授刻画了射影平坦且具有常数旗曲率的Randers度量[2]。在此之后,沈忠民教授与G.C.Yildirim合作,于2005年刻画了射影平坦且具有常数旗曲率的平方度量[3]。在上述研究基础上,李本伶与沈忠民教授合作,于2007年刻画了射影平坦且具有常数旗曲率的(α,β)-度量[4]。
为了区分芬斯勒度量和黎曼度量,E.Cartan引入了一个非黎曼几何量——Cartan张量,进而定义了平均Cartan张量。(平均)Cartan张量沿着测地线的变化率即为(平均)Landsberg曲率。再根据(平均)Cartan张量和(平均)Landsberg曲率的定义,芬斯勒几何学家们定义了“具有相对迷向(平均)Landsberg曲率的芬斯勒度量”。1975年,Numata证明了:定义在n(≥3)维流形上,满足条件K≠0(K表示旗曲率)的具有标量旗曲率的Landsberg度量一定是黎曼度量[5]。2003年,程新跃、莫小欢和沈忠民3位教授合作,给出了具有相对迷向平均Landsberg曲率且具有标量旗曲率的芬斯勒度的旗曲率量满足的一组微分方程[6]。2008年,程新跃等刻画了具有相对迷向平均Landsberg曲率的(α,β)-度量[7]。
这自然引导我们去研究射影平坦且具有相对迷向平均Landsberg曲率的(α,β)-度量。
本文首先刻画了射影平坦的弱Landsberg的(α,β)-度量,并得到了如下定理。
定理1 设F=αφ(s),s=β/α,是定义在n维流形M上的(α,β)-度量。若F为射影平坦的弱Landsberg度量,则F必为下列情形之一:
①F是黎曼度量。
②F是Berwald度量。此时α一定具有常数截面曲率,记为μ。进一步地:
若μ=0,则F为局部Minkowski度量;若μ≠0,则β可由下式确定:
其中Q=(qij)是一个反对称矩阵,v=(vi)为Rn中的常向量。
更进一步地,刻画射影平坦且具有相对迷向平均Landsberg曲率的(α,β)-度量,并得到如下定理。
定理2 设F=αφ(s),s=β/α,是定义在n(≥3)维流形M上的(α,β)-度量,其中φ=φ(s) 是关于s的多项式。若F射影平坦且具有相对迷向平均Landsberg曲率,则F必为下列情形之一:
①F是射影平坦且具有迷向S曲率的Randers型度量。
②F是Berwald度量。此时α一定具有常数截面曲率,记为μ。更进一步地:
若μ=0,则F为局部Minkowski度量;若μ≠0,则β可由下式确定:
其中,Q=(qij)是一个反对称矩阵,v=(vi)为Rn中的常向量。
需要说明的是:由文献[7]中结果可知,定理2①中的Randers度量可完全被确定。
1 预备知识
本节将介绍一些必备的知识,为本文的研究做准备。
首先给出芬斯勒度量的定义。
设M是一个n维光滑流形,F:TM→[0,+∞)是定义在其切丛上的非负函数。如果F满足如下条件:
① 光滑性:在带孔切丛TM{0}上,F(x,y)是C∞函数;
② 正齐次性:F=F(x,y)满足
F(x,λy)=λF(x,y),∀λ>0;
③ 正则性:对于任意非零向量y≠0,有
构成正定的矩阵,则称F为M上的一个芬斯勒度量。且将
g=gij(x,y)dxi⊗dxj
称为F的基本二次型或基本张量。
将具备芬斯勒度量的微分流形(M,F)称为芬斯勒流形或芬斯勒空间。
其次,在此给出测地系数的定义。
令F是定义在n为流形M上的芬斯勒度量。F的测地线可以由下述2阶微分方程组给出:
其中
且(gij)=(gij)-1。Gi称为F的测地系数。
然后,给出Cartan张量的定义。
设(M,F)是一个n为芬斯勒流形,Cartan张量C是定义在π*TM(M上的切丛在自然的丛投影下的拉回切子丛)上的三阶对称张量:
C∶=Cijk(x,y)dxi⊗dxj⊗dxk
其中
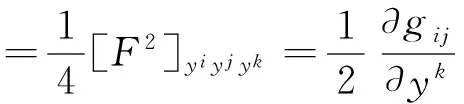
(2)
Cartan张量的平均值I称为平均Cartan张量,其定义为
I∶=Iidxi,Ii=gjkCijk
(3)
(平均)Cartan张量沿测地线的变化率即为(平均)Landsberg曲率。令
Ly(u,v,w)∶
其中:c(t)是F的一条测地线;U(t),V(t)和W(t)是沿c(t)的平行向量场。显然Ly为零阶正齐次,则
L∶={Ly}y∈TM{0}
称为Landsberg曲率。如果一个芬斯勒度量满足L=0,则称之为Landsberg度量。令
Jy(u)∶
其中(gij)=(gij)-1,则
J∶={Jy}y∈TM{0}
称为平均Landsberg曲率。如果一个芬斯勒度量满足J=0,则称之为弱Landsberg度量。更一般地,对于定义在流形M上芬斯勒度量F,若存在M上的标量函数c(x),使得J+c(x)FI=0,则称F是具有相对迷向的平均Landsberg曲率的芬斯勒度量。
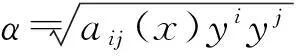
F∶=αφ(s),s=β/α
其中φ=φ(s)是定义在开区间(-b0,b0)的C∞函数。
对任意给定的(α,β)-度量,根据线性代数的知识可以直接计算得[8]:
det(gij)=φn+1×(φ-sφ′)n-2×
[(φ-sφ′)+(b2-s2)φ″]×det(aij)
(4)
其中b∶=‖βx‖α φ(s)>0 φ(s)-sφ′(s)+(ρ2-s2)φ″(s)>0 ‖s‖≤ρ (5) 在式(5)中,令‖s‖=ρ可得: φ(s)-sφ′(s)>0,‖s‖ (6) 本文主要研究正则的(α,β)-度量。 记“;”为关于α的黎曼联络的协变导数。令 bi;jθj∶ 可得: (7) ri∶=bjrji,si∶=bjsji 其中(aij)∶=(aij)-1且bj∶=ajkbk。 根据式(3)和式(4),可以直接计算出(α,β)-度量的平均Cartan张量[7]: φ-sφ′)·hi (8) 其中 Δ∶=1+sQ+(b2-s2)Q′, Φ∶=-(nΔ+1+sQ)(Q-sQ′)- (b2-s2)(1+sQ)Q″ yi=aijyj hi=bi-α-1syi 文献[7,9]中,程新跃及李本伶、沈忠民给出了(α,β)-度量的平均Landsberg曲率,其表达式可由式(9)给出。 (9) 其中 Ψ1∶ 令J∶=Jjbj。由式(9)可以计算得: αΨ2(r0+s0)} (10) 其中 Ψ2∶ Berwald度量是芬斯勒几何中的一类重要度量。一个芬斯勒度量F是Berwald度量的充分必要条件是F与某一黎曼度量有相同的测地系数。本节着重分类和刻画射影平坦的Berwald-(α,β)-度量,并得到了如下定理: 定理3 令F=αφ(β/α)为定义在n维流形M上的射影平坦的(α,β)-度量。若F为Berwald度量,则α一定具有常数截面曲率,记为μ。进一步地: 若μ=0,则F为局部Minkowski度量;若μ≠0,则β可由下式确定: 其中Q=(qij)是一个反对称矩阵,v=(vi)为常向量。 为了证明定理3,需要如下2个引理: 引理1[8]令F是定义在流形M上的芬斯勒度量。F射影平坦的充分必要条件是存在TM上的标量函数P使得: Gi=Pyi (11) 其中P=P(x,y)满足: (12) 定理3的证明: 由于F为Berwald度量,所以易证bi;j=0,从而 rij=0,sij=0 由式(7)可得: (13) 情形1μ=0 根据式(1)可知: 此时,式(13)可以写为 (14) 易知bi=constant,所以β=〈b,y〉,其中b=(bi)∈Rn为常向量。在这种情况下,F为局部Minkowski度量。 情形2μ≠0 此时 容易发现: 此时,α的Christoffel记号可以表示为: (15) 根据式(13)和式(15)可得: (16) 显然,通过式(16)可得: (17) (18) 再根据式(18),可以计算出[10] 这表明mi对x的二阶偏导数恒为0。所以:mi关于x是一阶线性的[10],即mi=qijxj+vi。其中Q=(qij)为n阶常矩阵,v=(vi)为n维常向量。更进一步地,由式(18)可知:Q=(qij)是一个反对称矩阵,所以 进而有 本节将证明定理1。为了完成这一目标,需要如下的一些引理: 一方面,需要运用弱Landsberg度量的一些性质。 引理3[9]令F=αφ(β/α)是定义在2维流形上的(α,β)-度量。若F是弱Landsberg度量,则F是Berwald度量。 引理4[9]令F=αφ(β/α)是定义在n(≥3)维流形M上的(α,β)-度量。F是弱Landsberg度量的充分必要条件是:β满足 sij=0 rij=k(b2aij-bibj)+σbibj (19) 其中k=k(x),σ=σ(x)是流形M上的标量函数。并且φ=φ(s)满足 kΨ1+sσΨ3=0 (20) 其中 Ψ3∶ 另一方面,需要利用(α,β)-度量的一些性质。 根据Deicke定理可知:一个芬斯勒度量F为黎曼度量的充分必要条件是I=0。再通过式(8),可得所需的下述引理。 引理5[7]一个(α,β)-度量F为黎曼度量的充分必要条件是Φ=0。 引理6[11]对于(α,β)-度量F=αφ(β/α),若φ=φ(s)满足Ψ1=0,则F是黎曼度量。 引理7[9]对于(α,β)-度量F=αφ(β./α),若 Φ≠0,sij=0, rij=k(b2aij-bibj)+σbibj 则Q=q1s,其中q1是一个常数。 引理8[12]对于(α,β)-度量F=αφ(β/α),若Q-sQ′=0或Q=q1s,其中q1是一个与s无关的数,则 φ 其中k1,k2是与s无关的数。此时F为黎曼度量。 定理1的证明: 令F=αφ(β/α)是一个弱Landsberg度量。 1) 当n=2时。由引理3可知F是Berwald度量。再根据定理3可以确定F。 2) 当n≥3时。根据引理4可得β满足式(19)且φ=φ(s)满足 kΨ1+sσΨ3=0 ①Φ=0。通过引理5可知F为黎曼度量。 ②Φ≠0。 k=0且σ=0。由引理4可知sij=0且rij=0,所以bi; j=0,此时F为Berwald度量。再由定理5可以确定F。 k≠0且σ=0。根据引理4可得Ψ1=0。进而由引理6得出F为黎曼度量。 k=0且σ≠0。通过引理4可以发现sij=0,rij=σbibj。进而由引理7和引理8可以得出F为黎曼度量。 k≠0且σ≠0。由引理4可知sij=0,rij=k(b2aij-bibj)+σbibj。再通过引理7和引理8可以得出F为黎曼度量。 证明完毕。 本节将证明定理2。为了完成这一目标,需要如下2个引理。 引理9[13]令F=αφ(β/α)是定义在n(≥3)维流形M上的非Randers型的(α,β)-度量,此时φ=φ(s)是关于s的多项式。若F具有相对迷向平均Landsberg曲率,即J+c(x)FI=0,则F为Berwald度量。 引理10[14]对于定义在n维流形M上的Randers度量F=α+β,下列条件是等价的:①J+c(x)FI=0; ②S=(n+1)cF。其中c=c(x) 是流形M上的标量函数。 定理2的证明: 令F=αφ(β/α)是射影平坦F具有相对迷向平均Landsberg曲率的(α,β)-度量,其中φ=φ(s) 是关于s的多项式。 1)F不是Randers型的芬斯勒度量。根据引理9可知:F是Berwald度量。再通过定理3可以确定F。 [1] BERWALD L.Uber die n-dimensionalen Geometrien konstanter Krummung,in denen die Geraden die kurzesten sind[J].Math Z,1929,30:449-469. [2] SHEN Z.Projectively flat Randers metrics with constant flag curvature[J].Math Ann,2003,325:19-30. [3] SHEN Z,YILDIRIM G C.On a class of projectively flat metrics with constant flag curvature[J].Canad J Math,2008,60(2):443-456. [4] Li B,SHEN Z.On a class of projectively flat Finsler metrics with constant flag curvature[J].International Journal of Mathematics,2007,18(7):1-12. [5] NUMATA S.On Landsberg spaces of scalar curvature[J].J Korea Math Soc,1975,12:97-100. [6] CHENG X,MO X,Shen Z.On the flag curvature of Finsler metrics of scalar curvature[J].J of the London Math Soc,2003,68(2):762-780. [7] CHENG X,WANG H,WANG M.(α,β)-metrics with relatively isotropic mean Landsberg curvature[J].Publ Math Debrecen,2008,72:475-485. [8] CHERN S S,SHEN Z.Rieman-Finsler Geometry[M].Singapore:World Scientific,2005. [9] LI B,SHEN Z.On a class of weak Landsberg metrics[J].Science in China Series A,2007,50,75-85. [10]BAO D,ROBLES C,SHEN Z.Zermelo Navigation on Riemannian manifold[J].J Diff Geom,2004,66:762-780. [11]CHENG X,LI X,ZHOU Y.On confor- mally flat (α,β)-metrics with relatively isotropic mean Landsberg curvature[J].Publ Math Debrecen,2014,85(1/2):131-144. [12]SHEN Z.On a class of Landsberg metrics in Finsler geometry[J].Canad J Math,2009,61(6):1357-1374. [13]CHENG X,ZOU Y.The generalized unicorn problem in Finsler geometry[J].Diff Geom-Dynamial system(DGDS),2015,17:38-48. [14]CHENG X,SHEN Z.Randers metrics with special curvature properties[J].Osaka J of Math,2003,40:87-101. (责任编辑 刘 舸) On Projectively Flat (α,β)-Metrics with Relatively Isotropic Mean Landsberg Curvature CHENG Xin-yue, LIU Shu-hua (College of Science, Chongqing University of Technology, Chongqing 400054, China) We studied projectively flat (α,β)-metrics in the form ofF=αφ(β/α), whereαis a Riemannian metric andβis a 1-form on the manifold. We classified projectively flat weak Landsberg (α,β)-metrics. Further, we classified projectively flat (α,β)-metricF=αφ(β/α), whereφ=φ(s) is a polynomial ins, with relatively isotropic mean Landsberg curvature. projectively flat Finsler metrics; (α,β)-metrics; Landsberg curvature; mean Landsberg curvature 2016-05-20 基金项目:国家自然科学基金资助项目(11371386) 程新跃(1958—),男,重庆人,博士,教授,主要从事微分几何及其应用研究;刘树华(1990—),男,湖北人,硕士研究生,主要从事微分几何及其应用研究,E-mail:12612954@qq.com。 程新跃,刘树华.射影平坦且具有相对迷向平均Landsberg曲率的(α,β)-度量[J].重庆理工大学学报(自然科学),2017(2):140-145. format:CHENG Xin-yue, LIU Shu-hua.On Projectively Flat (α,β)-Metrics with Relatively Isotropic Mean Landsberg Curvature[J].Journal of Chongqing University of Technology(Natural Science),2017(2):140-145. 10.3969/j.issn.1674-8425(z).2017.02.023 O186.1 A 1674-8425(2017)02-0140-06

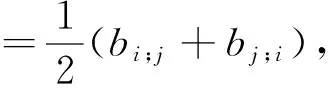

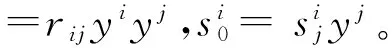
2 射影平坦的Berwald-(α, β)-度量
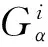

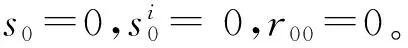


3 定理1的证明
4 定理2的证明

