带负顾客、中途退出及反馈的M/M/1/N工作休假排队
2017-03-16朱翼隽
王 莉,朱翼隽
(1. 宿迁学院 数学系,江苏 宿迁 223800; 2. 江苏大学 理学院,江苏 镇江 212013)
带负顾客、中途退出及反馈的M/M/1/N工作休假排队
王 莉1,朱翼隽2
(1. 宿迁学院 数学系,江苏 宿迁 223800; 2. 江苏大学 理学院,江苏 镇江 212013)
本文在带有负顾客的M/M/1/N多重工作休假排队系统的背景下,同时引入了不耐烦和反馈策略后进行了研究。首先利用马尔可夫过程方法给出了稳态下概率满足的方程组,接着利用矩阵理论求出了稳态下矩阵形式的概率解,并得到了稳态下的队长均值、等待队长均值等一些性能指标。最后,利用数值模拟分析了系统参数对平均队长的影响。
负顾客;中途退出;反馈;多重工作休假;矩阵几何解法
0 引言
以往所研究的休假排队系统,服务员在休假期不工作,这类休假系统称为经典休假排队,已经得到了较完善的的研究和发展。然而,在很多实际休假模型中,为提高服务效率往往规定休假时服务员不完全停止工作,而是以低于正常的服务率工作。比如在医院,休假时不会都休息,有部分工作人员仍继续值班,这是一种半休假策略称为工作休假,Liu Wengyuan等[1],Wu De’an等[2]和Tian N等[3]分别研究了这类工作休假排队模型。当工作休假期服务员的服务率降为零时,就变成经典休假排队模型。目前,工作休假排队在国内外成为专家研究的热点。在此类模型中也会常遇到服务系统中出现对服务台的外来援助,我们称之为负顾客,它的到来会抵消掉在被服务的顾客,当负顾客到达系统时无顾客,它会自行离开,徐祖润等[4],Krishna Kumar B等[5]和郭小琼等[6]分别研究了三类不同的带负顾客的工作休假排队模型,从中求出了稳态时的队长分布和随机分解结果及平均队长等一些重要的性能指标,为继续深入研究此类模型奠定了理论和数据基础。现如今,带有中途退出这种不耐烦策略的排队系统也成为许多学者研究的又一课题。其中Haight[7]对带有中途退出的M/M/1排队系统做了详细地研究。周宗好等[8]讨论了带有止步和中途退出策略的Mx/M/1/N单重工作休假排队系统。他们都将带中途退出策略的这些模型利用马氏理论和矩阵方法给出了系统的稳态队长分布或稳态概率及一些均值指标。此外,反馈机制也是当今排队论研究中的又一热点,以Bernoulli反馈为典型,其在计算机分时操作体系和无线电通讯网络体系中有着普遍应用。加入反馈的各类模型已被广泛研究,顾庆凤等[9]和刘红丹等[10]分别在单服务台和多服务台休假系统中加入了负顾客和Bernoulli反馈策略,通过研究得到了稳态下应满足的条件和分布的向量形式等指标。综合目前的各类研究,将负顾客、中途退出及反馈和工作休假各特点都结合的文章还不多,本文首次将其结合在一起研究了带有负顾客和中途退出及反馈的M/M/1/N多重工作休假排队系统。
1 模型描述
现对本模型做如下规定:
(1)假定系统中含有正、负两类顾客且为单服务台系统,一次只服务一位顾客,系统中最多可容纳顾客数为N,即一旦正顾客量达到N个,再到达的正顾客就将消失。正、负顾客均按参数各为λ和ε的泊松流到达。负顾客会按一比一消除排在首位的正顾客,在无正顾客时,到来的负顾客自行移除。
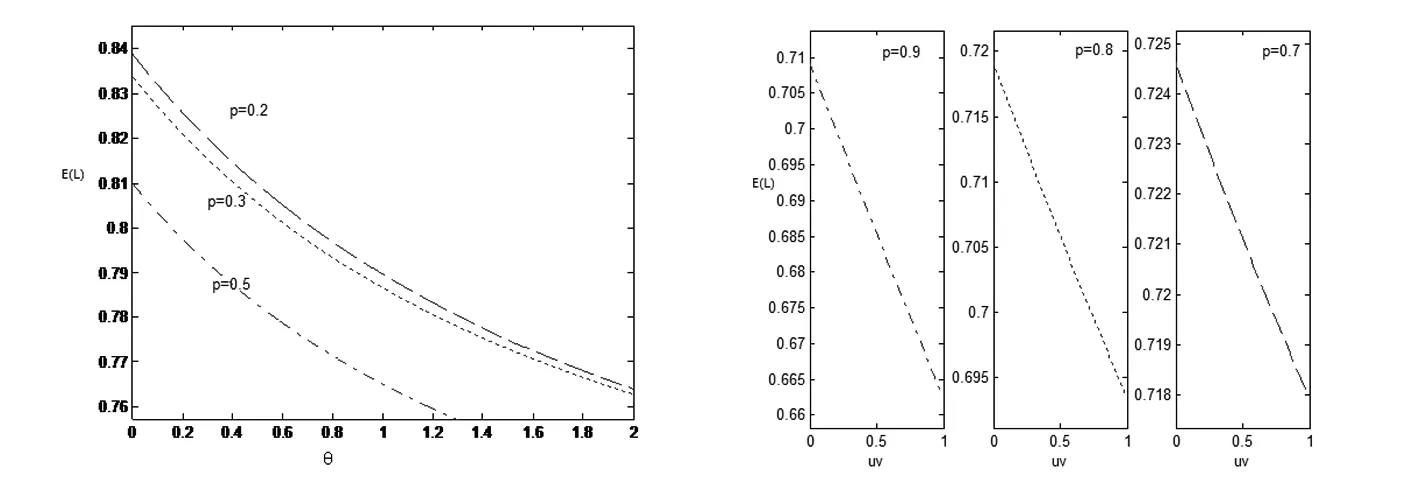
(2)系统分为工作休假和忙期两个阶段。当系统内无顾客时,服务台会进入一个休假时间V服从参数为θ负指数分布的工作休假期,此时顾客被以较低的服务率μv服务。如果某次假期结束时系统内仍为空,则按相同的方式继续休假;否则服务台将停止工作休假转为忙期,并以正常效率μb(μb>μv)服务正顾客,直到系统再次为空。服务台在两个阶段的服务时间均服从负指数分布。服务完的顾客按概率p(0 (3)顾客进入系统由于排队等待,根据队长的大小而产生不同程度的厌烦情绪常会在未接受服务的情况下中途退出。系统忙时顾客的中途退出率 r(n)=(n-1)α,2≤n≤N 休假时顾客的中途退出率 r(n)=nα,1≤n≤N 其中,α规定为中途退出前顾客在系统中等待时间所服从的负指数分布的参数。 (4)假定服务过程与到达过程且以上各随机变量间均相互独立,按到达的先后顺序服务。 令N(t)表示时刻t系统中的顾客数,J(t)表示时刻t服务员的工作状态,定义: 则{N(t),J(t),t≥0}为二维马尔可夫过程,状态空间为 Ω={(n,0):0≤n≤N∪(n,1):1≤n≤N} 定义系统的稳态概率: 则其满足的方程组如下: (pμv+ε+α)P0(1)+(pμb+ε+α)P1(1)=(λ+θ)P0(0) (1) [(1-p)μv+λ]P0(n-1)+[pμv+ε+(n+1)α]P0(n+1)= [μv+ε+θ+nα+λ]P0(n),1≤n≤N-1 (2) [(1-p)μv+λ]P0(N-1)=(pμv+ε+θ+Nα)P0(N) (3) θP0(1)+(pμv+ε+α)P1(2)=(μb+ε+λ)p1(1) (4) θP0(n)+[(1-p)μv+λ]P1(n-1)+(pμb+ε+Nα)P1(n+1)= [μb+ε+(n-1)α+λ]P1(n),2≤n≤N-1 (5) θP0(N)+[(1-p)μb+λ]P1(N-1)=[pμb+ε+(N-1)α]P1(N) (6) 上述(1)~(3)式表示顾客在假期进入系统时状态的变化,(4)~(6)表示处在正常忙期的状态情况。 将转移概率矩阵分块如下: A1= A2= 证明 参见北京大学数学系编写的《高等代数》第二版[11]。 证明 记DN=|A2|,将DN的第二列到第N列都加到第一列,再按第一列各元素展开可得DN=-(pμb+ε)D-1,按上述展开降阶法依次降阶可得 DN-i=-(pμb+ε+iα)DN-i-1,1≤i≤N-2 D1=-[pμb+ε+(N-1)α] 定理3 系统的稳态概率为 P0(0)=δ (7) (8) (9) 注:εn(1≤n≤N)为N维单位列向量,eN+1和eN分别是元素全为1的N+1维、N维列向量,e表示元素全为1的2N+1维列向量。 证明 令稳态向量P0=(P0(0),P0(1),…,P0(N)),P1=(P1(1),…,P1(N)) 记P=(P0,P1),则其满足 (10) 将(10)式表示成分块形式 (11) P0eN+1+P1eN=1 (12) 由(11)式可得 (15) 展开得 由上式可得 (16) 从而 (17) 同理由(14)式和(16)式有 (18) 将(17)和(18)式代入(12)式可得 (19) 将(19)式分别代入(17)式和(18)式整理得到系统稳态概率为 3)平均等待队长 4)平均队长 5)平均中途离去率 6)顾客的消失率 下面给出系统稳态队长随休假率θ和工作休假期服务率uv变化的情况。 图1 θ对平均队长E(L)的影响 图2 uv对平均队长E(L)的影响 观察图1知,取μv=0.2,系统稳态平均队长E(L)随休假率θ增大而逐渐变小。当取定θ值时,显然p值越大,E(L)越小,说明平均顾客数越少,平均离去率越大。 由图2可知,取θ=2时,E(L)随工作休假期服务率μv的增加而减小。在取定μv值时,p取值越大,E(L)越小,而顾客离去率越大,即顾客因不耐烦而离开系统的人数越多。 通过以上分析,研究此类模型时可以合理地变化参数指标,取适当的值可使系统平均稳态队长达到最小,同时假期和忙期服务率较高来节省顾客的排队时间及系统的服务成本,使排队系统尽可能达到最优化。 本文结合排队系统在实际中可能出现的情况,在具有有限容量的多重工作休假排队系统中同时引入负顾客、中途退出不耐烦策略和反馈机制三个条件,相比以前文献中的所研究的模型更复杂,更具体,对这种新模型采用了拟生灭过程的理论方法进行研究,运用矩阵几何解法得到了系统的稳态概率,并由此获得了本模型的一些重要指标,如忙期和休假期的概率、平均队长和平均等待队长,离去率等,为实际中出现的此类模型的研究提供了理论数据。最后,对本模型又做了具体的数值模拟,得到了重要指标平均队长随参数的变化情况,为进一步优化模型提供了数据实例。 [1]LiuWengyuan,XuXiuli,TianNaishuo.Stochasticdecompositionsinthequeuewithworkingvacations[J].OperationsResearchLetters,2007(5):595-600. [2]WuDe’an,TAKAGIH.M/G/1queuewithmultipleworkingvacations[J].PerforEval,2006(7):654-681. [3]TianN,ZhangZG.AnalysisoftheM/G/1queuewithexponentiallyworkingvacationsamatrixanalyticapproach[J].QueueingSystems,2009(2):139-166. [4] 徐祖润,李敏捷,朱翼隽.带有负顾客的M/M/C多重工作休假排队[J].数学的实践与认识,2011(11):91-98. [5]KrishnaKumarB,ArivudainambiD,KrishnamoorthyA.SomeresultsonageneralizedM/G/1feed-backqueuewithnegativecustomers[J].OperationsResearchLetters,2006(1):277-296. [6] 郭小琼,马占有.带负顾客的GI/Geom/1工作休假排队[J].郑州大学学报:理学版,2011(4):28-32. [7]HaightFA.Queuingwithreneging[J] .Metrika,1959(2):186-197. [8] 周宗好,顾庆凤,余君,等.带有止步与中途退出策略的单重工作休假排队系统[J]. 数学的实践与认识,2014(7):125-133. [9] 顾庆凤,朱翼隽. 带有负顾客且具有Bernoulli反馈的M/M/1工作休假排队[J].运筹与管理,2008(3):64-69. [10] 刘红丹,吕胜利,李丹丹.有负顾客且Bernoulli反馈的M/M/c工作休假排队系统[J].郑州大学学报:理学版,2013(2):14-18. [11] 北京大学数学系几何与代数教研室代数小组.高等代数(第二版)[M].北京:高等教育出版社,1988. (责任编辑:孙文彬) The M/M/1/N Working Vacation Queuing System with Negative Customers Reneging and Feedback WANG Li1, ZHU Yi-juan2 (1. Mathematic Department, Suqian College, Suqian Jiangsu 223800, China; 2. Faculty of Science, Jiangsu University, Zhenjang Jiangsu 212013, China) In this paper, the renege and feedback are introduced to an multiple working vacation queuing system with negative customers. Firstly, equations for steady-state probability are given by the Markov process method. Subsequently, by using matrix theory, the matrix form solution of steady-state probability is derived; some performance indicators of the system such as the steady-state average queue length, waiting queue length in the system are also obtained. Finally, the effects of the system parameters on the expected queue length are investigated by numerical simulation. negative customers; renege; feedback; multiple working vacations; matrix-geometric solution 2016-09-26 王莉(1980-),女,山东武城人,讲师, 在读硕士,主要从事排队论等研究。 O A 1009-7961(2017)01-0095-062 稳态概率方程组的建立

3 稳态概率的矩阵几何解








4 系统的一些性能指标
5 数值例子
6 结论
