再议ax=logax(a∈(0,1))的解

江西省临川一中 (344100) 陆继承 张珍珍

再议ax=logax(a∈(0,1))的解

江西省临川一中 (344100) 陆继承 张珍珍

对于ax=logax(a∈(0,1))的解的讨论，似乎一直都没有停止过，究其原因，主要是ax=logax(a∈(0,1))中的两个简单初等函数图像画在同一个坐标系里，直观判断很容易产生误解，很多没有深入讨论的师生以为只有一个解，其实不然.不过到目前为止，对于ax=logax(a∈(0,1))的解的个数的讨论结果已经没有什么争议了，但对于这个问题的证明，许多同行给出了独到的见解，这里笔者效仿各位同行前辈，给出了自己的两种证明过程，请各位同行们批评指正.

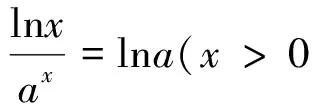
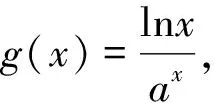
我们先分析函数y=xlnx，有y′=lnx+1，则

①当a∈[e-e,1)时，-e≤lna<0，所以有

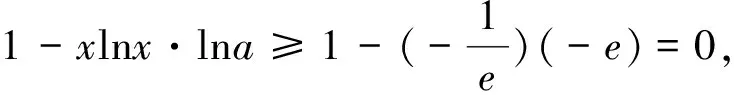
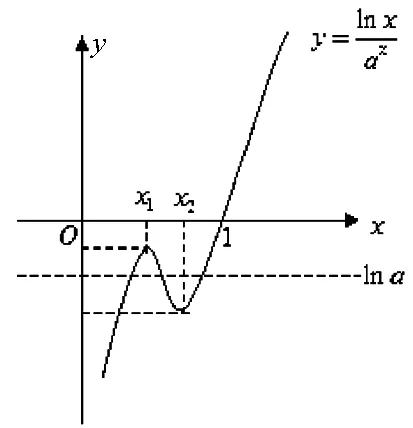
图1

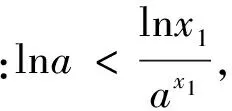
x1lna>lnx1+2ln(-lnx1)，

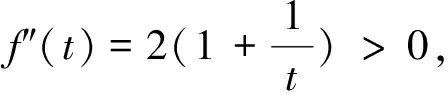
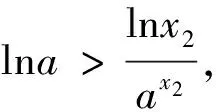
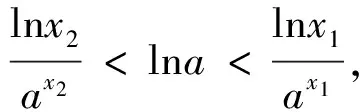
综上：当a∈(0,e-e)时，ax=logax有3个解；

当a∈[e-e,1)时，ax=logax有1个解.

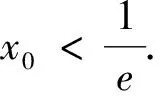
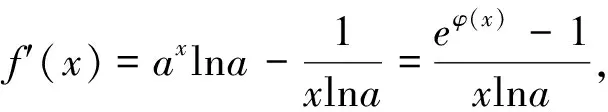
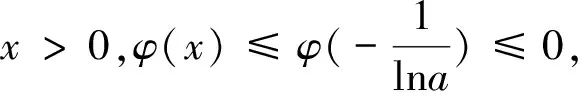
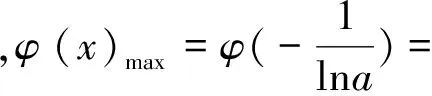
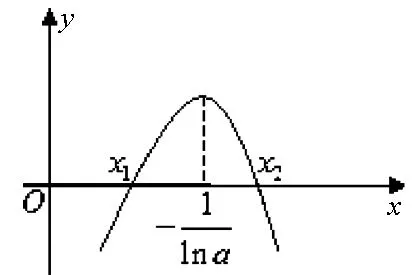
图2

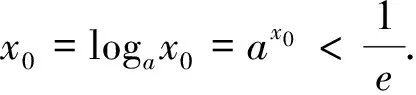
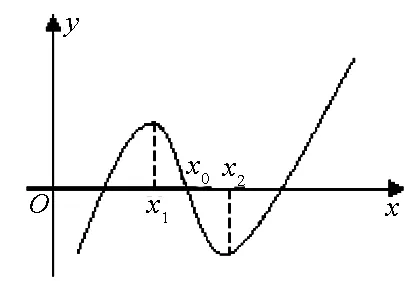
图3

再令t=lnx0∈(-∞,

综上：当a∈(0,e-e)时，f(x)=ax-logax=0有3个解；

当a∈[e-e,1)时，f(x)=ax-logax=0有1个解.