对一类环形染色问题的探究
2017-03-16江西省萍乡市上栗中学337009黄玉娇
江西省萍乡市上栗中学 (337009) 黄玉娇
对一类环形染色问题的探究
江西省萍乡市上栗中学 (337009) 黄玉娇
题1 (2003年全国高考理科第15小题)某城市在中心广场建造一个花圃,花圃分为6个部分(如图1),现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有多少种?
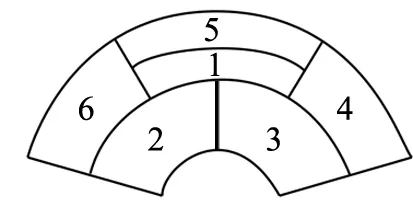
图1
原解答如下:从题意来看6部分种4种颜色的花,又从图形看知必有2组同颜色的花,可从同颜色的花入手分类求解.
(1)②与⑤同色,则③⑥也同色或④⑥也同色,所以共有N1=4×3×2×2×1=48种;
(2)③与⑤同色,则②④或⑥④同色,所以共有N2=4×3×2×2×1=48种;
(3)②与④且③与⑥同色,则共有N3=4×3×2×1=24种.
∴共有N=N1+N2+N3=48+48+24=120种.

图2
题2 (2001全国高中数学联赛第12题)在一个正六边形的六个区域栽种观赏植物(如图2),要求同一块中种同一种植物,相邻两块种不同的植物,现有4种不同的植物可供选择,则有多少种栽种的方案?
原解答如下:为了叙述方便起见,我们给六块区域依次标上字母A、B、C、D、E、F.按间隔三块A、C、E种植植物的种数,分以下三类.
(1)若A、C、E种同一种植物,有4种种法.当A、C、E种植后,F可从剩余的三种植物中各选一种植物(允许重复),各有3种方法.此时共有4×3×3×3=108种方法.


根据加法原理,总共有N=108+432+192=732种栽种方案.
近年来,各类高考复习参考资料中涉及的田字种草,雨伞着色等,其中的问题都是一种环形着色问题.这些问题所提供的参考答案都是一些利用分类、分步,排列组合原理的求法,其计算之复杂,难度之大,令广大学生难以接受.本文介绍一种利用递推数列导出通项公式的方法,给出环状着色问题的统一解法.
先看题1.首先,第1块地上可以先种植,共有4种种法.余下的2-6块地就是一个五环着三色的问题.先瞻前不顾后,2,3,4,5,6块地的种植方法有3×24=48种,但这样下去,第6块有可能与第2块地同色,其效果上就好比四环种三色,设其方法数为a4,若第6块与第2块不同色,则是5环着3色问题,设其方法数为a5,这样由分步计数原理便有a5+a4=3×24=48,这里a4代表四环着3色,易知方法有3×2×2+3×2×1×1=18种,从而a5=30,本问题的最后结果是4×30=120种.
同样分析题2.设6环着4色方法有a6,5环着4色方法有a5,4环着4色方法有a4,3环着4色方法有a3,2环着4色方法有a2,则a2=4×3=12种,a3+a2=4×32,a3=36-12=24,a4+a3=4×33=108,从而a4=84,a5+a4=4×34,则a5=240,a6+a5=4×35,求得a6=972-240=732种.
一般地,下面我们探索一个n环土地着4色问题.
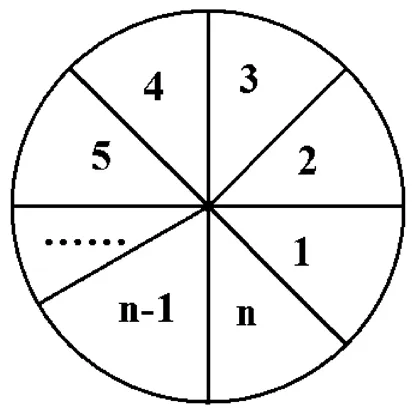
图3

引理 若一个组合数列{an+1-pan}是一个公比为q的等比数列,则组合数列{an+1-qan}必是一个公比为q的等比数列.
证明:假设有an+1-pan=q(an-pan-1)⟹an+1-qan=p(an-qan-1)即证.
特别地,当an+1-pan=c(c为常数),{an+1-an}必是一个以p为公比的等比数列.
由an+an-1=4×3n-1得an+1+an=4×3n,由上面的引理可知an+1-3an=(a3-3a2)×(-1)n-2=-12×(-1)n,上面两式相减可得4an=4×3n+12×(-1)n⟹an=3n+3×(-1)n.
这样便得出一个4色着n环,相邻区域不同色的方法总数an=3n+3×(-1)n.
类比上述方法,不难证明:m色着n环,相邻不同色颜色不一定用全的方法数为an=(m-1)n+(m-1)(-1)n.
证明:an+1+an=m(m-1)n-1,an+1-(m-1)an=[a3-(m-1)a2](-1)n-2,注意到a3=m(m-1)(m-2),a2=m(m-1),(-1)n-2=(-1)n,即可得an=(m-1)n+(m-1)(-1)n.
注:本文得到我校肖锋老师的指导,在此特别致谢!
