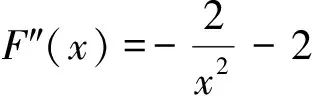看山是山，看山不是山，看山仍是山*——极值点偏移问题再探究

厦门大学附属实验中学 (363123) 田富德

看山是山，看山不是山，看山仍是山*
——极值点偏移问题再探究

厦门大学附属实验中学 (363123) 田富德

宋代禅宗大师青原行思提出参禅的三重境界：参禅之初，看山是山，看水是水；禅有悟时，看山不是山，看水不是水；禅中彻悟，看山仍是山，看水仍是水.

其实数学解题，特别是数学压轴题亦是这三重境界.本文以极值点偏移问题为例谈解数学压轴题的三重境界.

极值点偏移问题近几年倍受命题者的青睐，在各省市高考题、模拟题频繁出现，在2016年高考全国卷压轴题亦为极值点偏移问题.极值点偏移问题能成为高考考查的热点，是因为这类问题能较好考查学生的逻辑推理能力、数据处理能力、转化与化归思想、函数与方程思想等.

例1 已知函数f(x)=lnx-ax2，a为常数.

(Ⅰ)讨论f(x)的单调性；

(Ⅱ)若函数f(x)有两个零点x1,x2，证明：x1x2>e.

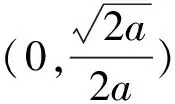
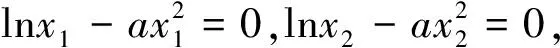
只需证g(t)>0，证明略.

以上证明是常见的利用零点消参的换元解法.初看此题第(Ⅱ)问，具备了极值点偏移问题的主要特征：其一，条件为双零点；其二，证明与两零点有关的不等式.看山是山，我们却不好用极值点偏移解题策略解此题.

我们注意到极值点偏移是研究两零点和的有关不等式，而本题则是研究两零点积的有关不等式，故我们自然将问题“x1x2>e”转化为“lnx1+lnx2>1”.但此时已转化为两零点的对数和有关的不等式，亦不能看作极值点偏移问题，看山不是山！

然而lnx1、lnx2亦可成为另一个函数的两零点，故我们可尝试换元将此题转化为极值点偏移问题.

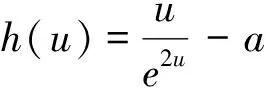
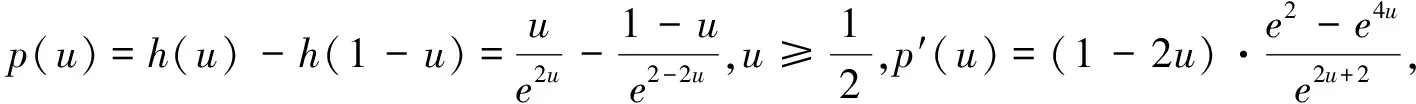
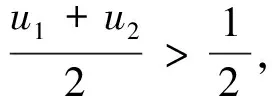
(Ⅰ)讨论f(x)的单调性；

(Ⅱ)若函数f(x)有两个零点x1,x2，其中a>0，证明：x1+x2<-ln2a.

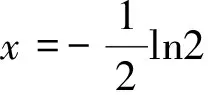
解：(Ⅰ)略；

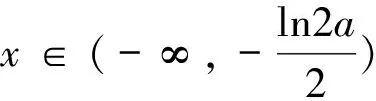
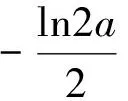
g″(x)=-4ae2x单调递减.

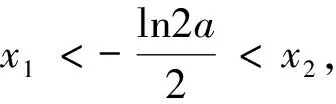
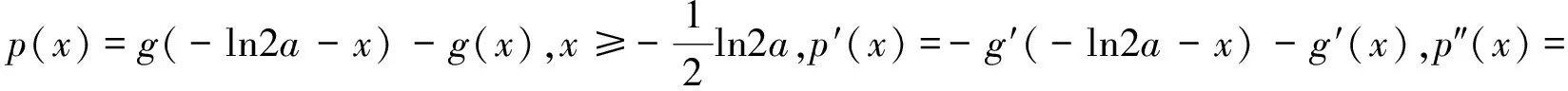
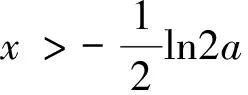
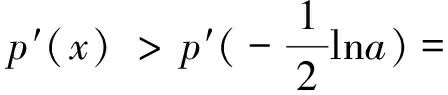
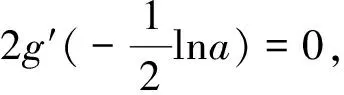
说明:本例解答在构造函数p(x)时，并未将g(x)的表达式代入，而是对函数p(x)进行抽象处理，在一定程度上减少了求导计算量.此法适用于构造函数的导函数较为复杂，求导不好判断正负，但要求g″(x)在定义范围内是单调的.

我们便可得到如下试题：

(Ⅰ)讨论f(x)的单调性；

(Ⅱ)若函数f(x)有两个零点x1,x2，其中a>0，证明：1

例3的结论是通过放缩而得到的，其中x1+x2>1的证明可以直接利用极值点偏移策略解题，亦为证明x1+x2<-2ln2a-1做好铺垫作用.

例4 已知函数f(x)=alnx-x，g(x)=x2-(1-a)x-(2-a)lnx，其中a∈R.

(Ⅰ)若g(x)在其定义域内为增函数，求实数a的取值范围；

(Ⅱ)若函数F(x)=f(x)-g(x)的图像交x轴于A,B两点，A,B的中点横坐标为x0，问F(x)的图像在点(x0,F(x0))处的切线能否平行于x轴？

分析：连续函数若有唯一极值点，那仅该极值点上所在位置的切线方能平行于x轴.题问点(x0,F(x0))处的切线能否平行于x轴，换句话说x0是否为极值点，极值点是否偏移.设函数的极值点为m，问题转化为m是否等于x0，若有偏移，则只需证x0>m或x0

解：(Ⅰ)a≥2；

当x∈(0,m)时，F′(x)>0，F(x)单调递增；当x∈(m,+∞)时，F′(x)<0，F(x)单调递减.

结合(*)，知x0不是极值点，故点(x0,F(x0))处的切线不能平行于x轴.

说明:本题的其他证法在本文略去，从表面看，本题与极值点偏移无关，深入分析亦为极值点偏移问题.所谓看山是山，看山不是山，看山还是山.即要对题设深入分析其本质，便可看山是山，看水是水.

学数学，要在压轴题上有所突破，必须建立起已知和未知的联系，建立起基本题型与创新题型的联系，做好基本方法和基本策略在创新试题迁移，弄清试题的多角度本质，每一个角度都可以是一种解题方法.

[1]刑友宝.极值点偏移问题的处理策略[J].中学数学教学参考：上旬，2014(7)：19-22.

[2]赖淑明.极值点偏移问题的另一本质回归[J].中学数学教学参考：上旬，2015(4)：49-51.

[3]田富德.以拐点偏移为背景的函数导数试题命制[J].中学数学研究(江西师大)：2016(2)：10-13.

[4]田富德.一道模拟题的加强与改编[J].中学数学研究(江西师大)：2016(4)：12-14.

* 注：本文系2015年度漳州市基础教育课程教学研究立项课题《高中数学解题教学现状与优化》阶段性研究成果.