对阿波罗尼斯圆的探究和应用
2017-03-16湖北省房县二中442100姚家成
湖北省房县二中 (442100) 姚家成
对阿波罗尼斯圆的探究和应用
湖北省房县二中 (442100) 姚家成
对典型问题的探究能够更进一步揭示问题的本质,使我们获得更好的解决问题的方法.例如高中数学人教A版必修2有这样两道相关习题:
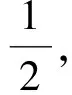
2.(第144页B组第2题)已知点M与两个定点M1,M2的距离的比是一个正数m,求点M的轨迹方程,并说明轨迹是什么图形(考虑m=1和m≠1两种情形).
这两个问题是从特殊到一般进行探究,可以得到一个结论:平面内与两个定点的距离之比为不等于1的正数的点的轨迹是一个圆.这样的圆被称为阿波罗尼斯圆(以下简称阿圆或定圆),有很多高考题是以它为背景命制的,在教学中进行一些相关的探究是很有必要的.
一、对一般情况的简解
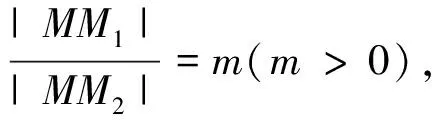
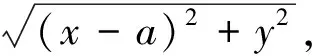
(1)当m=1时,图形为直线x=0;
二、从几何的角度进一步探究
这个问题值得探究的魅力就在确定性与任意性的辨证统一,定点和比值是确定的,圆的存在性是确定的,而圆上点的位置是任意的.定点、比值和圆是相伴共生,互为依存的,它们之间必有联系.因为在通常情况下我们看到一个圆,只是关注到它的圆心和半径,这两个定点和比值是隐藏着的.从变化中寻找出不变的性质,得到事物变化的规律,是我们思维的一种爱好.这里可能会想到下面的几个问题.
1.这两个定点和圆在位置上有什么关系,比值有没有几何意义?
2.当圆和定点确定后,圆上的任意一点对于给定的两个点所成的线段有没有一个确定的比值?
3.当圆和比值正常数确定后,能不能找到相应的两个定点?
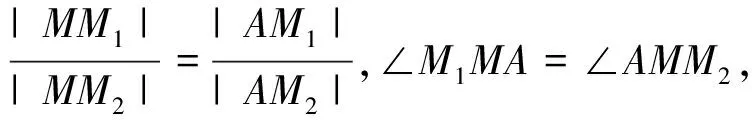
∠MM1C=∠CMN.同理可得∠CM1N=∠CNM,所以
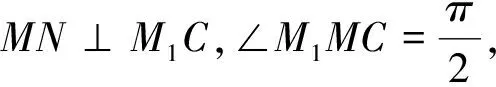
三、总结得出以下几条结论
为了便于区分,我们不妨把阿波罗尼圆称为定圆,可以理解为它是确定存在的;把M、C、N、M1这四个点所在的圆叫做伴生圆,可以理解为它是相对于定圆所生成的.因为M、N两点具有任意性,所以伴生圆是以阿圆外的那个定点和阿圆的圆心为弦的无数个圆.
(1)两定点和阿圆的圆心三点共线;
(2)两定点必为一个在阿圆内,另一个在阿圆外;
(3)过阿圆内的那个定点任意作一条弦,弦的两端点和阿圆的圆心以及阿圆外的那个定点这四个点共圆.
(4)以阿圆外的一个定点和阿圆的圆心为弦的圆与阿圆形成的公共弦必过在阿圆内的那个定点.
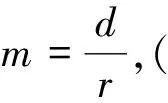
四、结论的应用
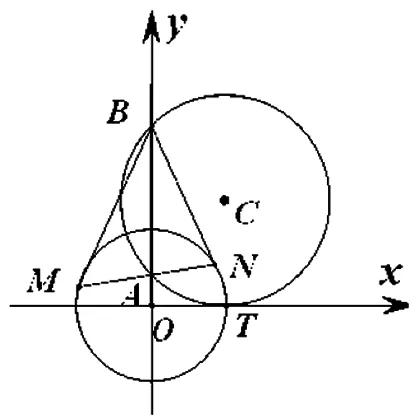
图2
1.(2015年高考数学湖北卷理科第14题)如图2,圆C与x轴相切于点T(1,0),与y轴的正半轴交于两点A、B(B在A的上方),且|AB|=2.
(1)圆C的标准方程为 ;
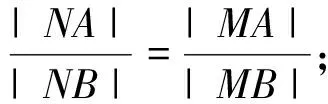
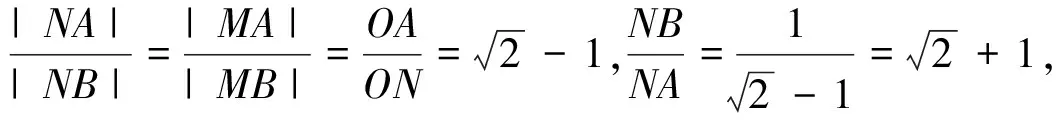
2.(2014年高考数学湖北卷文科第17题)已知圆O:x2+y2=1和点A(-2,0),若定点B(b,0)(b≠-2)和常数λ满足:对圆O上任意一点M,都有|MB|=λ|MA|,则(1)b= ;(2)λ= .
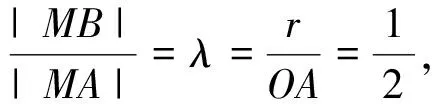
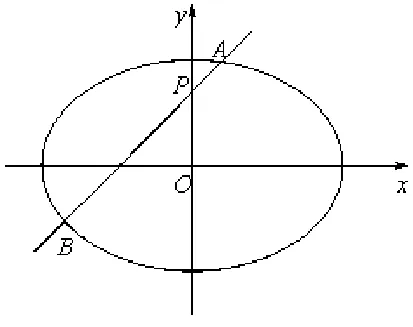
图3
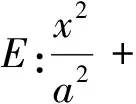
(1)求椭圆E的方程;
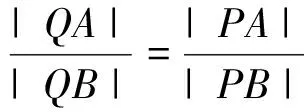
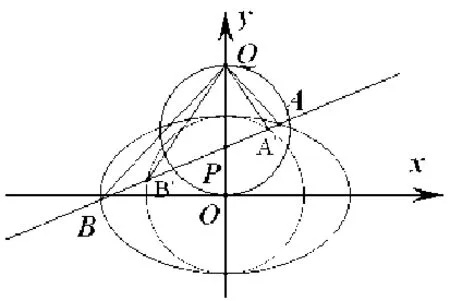
图4
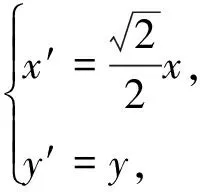
以上探究了阿波罗尼斯圆中的两个定点与动点的位置关系,特别是指出了定比值的一个几何意义,给我们解决与此相关的问题带来了很大的方便.这种利用课本中的题目进行探究得到一般性结论,进而解决高考中的较复杂的题目的方法,学生也是很感兴趣的.
