近年高考题中含参不等式恒成立问题的求解策略
2017-03-16广东省广州市恒福中学510075张美钰
广东省广州市恒福中学(510075) 张美钰
近年高考题中含参不等式恒成立问题的求解策略
广东省广州市恒福中学(510075) 张美钰
恒成立问题,是指在综合给定的范围内无论如何变化,某些数学问题的结论都不会发生任何改变.高中数学的恒成立问题是高考的一种重要题型,它涉及到函数、数列、不等式、导数等诸多方面的知识,同时考查了学生分析问题、解决问题、综合驾驭知识的能力.求解含有参数的恒成立问题是常见的题型,也是高考的热点.这类问题既含参数又含变量,可以考察到学生的思维能力和对数学知识的融会贯通的情况,在近年高考中出现频率较高.本文根据近三年的高考题总结了三种含参不等式恒成立问题的求解策略.
策略一、分离变量求解
1.(2016年江苏高考卷文理第 19题)已知函数f(x)=ax+bx(a>0,b>0,a/=1.b/=1).
(i)求方程f(x)=2的根;
(ii)若对于任意x∈R,不等式f(2x)≥mf(x)-6恒成立,求实数m的最大值;
(2)(略)

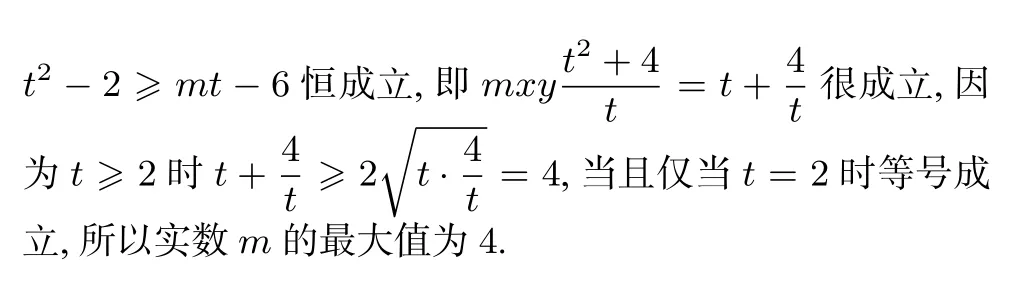
对于一些含参的不等式恒成立问题,如果能够将不等式进行同解变形,将不等式中的变量和参数进行分离,即使变量和参数分别位于不等式的左、右两边,那么通过求函数值域的方法将问题化归为解关于参数的不等式问题.应该说,这种解题思想是高中比较常规的一种思想.一般地有:

2.(2014年辽宁高考文科第12题、理科第11题)当x∈[-2,1]时,不等式ax3-x2+4x+3≥0恒成立,则实数a的取值范围是( )

此题的解决思想仍是分离变量,将不等式恒成立问题转化为函数的最值与参量的大小比较,而此题要求在分离变量时对x的范围进行分类讨论,否则会出错.
策略二、构造函数求解
(1)求证: f(x)≤0;


x (0,x0) x02 g′(x) + 0 -g(x)↗↘

当参数难以分离时,可以通过构建函数来解决.我们知道,函数概念是高中数学的一个很重要的概念,其思想和方法已经渗透到数学的各个分支.在有些数学问题上中,通过观察数式特点,构造适当的数学模型,然后通过研究此函数性质来确定参数的取值范围.
4.(2016年全国新课标 I卷文第 12题)若函数f(x)=x-+asinx在(-∞,+∞)单调递增,则 a的取值范围为( )


此题作为选择题的压轴题,并没有直接给出一个二次函数考查,而通过换元构造二次函数是求解本题的关键,考生需要熟悉基本原理,才可以在遇到生疏或繁难的问题,通过这些问题与基本问题的关系,“化生为熟,化繁为简”解决问题.二次函数型恒成立问题的具体解决需要根据函数性质、图像全面讨论x2的系数、对称轴、Δ值符号等解题.
一般地,二次函数型的恒成立问题有以下类型:
(1)类型1: 设 f(x)=ax2+bx+c(a/=0), f(x)>0(x∈R)恒成立 ⇐⇒ a>0且Δ<0;
(2)类型2: 设f(x)=ax2+bx+c(a/=0)

策略三、逐段筛选法求解
5.(2016年四川高考卷理21题)设函数f(x)= ax2-a-lnx,其中a∈R.
(1)讨论f(x)的单调性;


本题对a进行分类讨论,逐段筛选出符合条件的a的范围.求解的办法是对函数(或构造的函数)求导,然后结合单调性等验证不等式是否恒成立.这种解法既考查对不等式恒成立条件正面的探究过程,又考查不等式恒成立的否定过程,对考生能力要求高,命题者把其作为高考压轴题的首选题型,活跃在高考试题中多年.其姐妹题为2016高考卷四川文第21题:
设函数f(x)=ax2-a-lnx,g(x)=其中a∈R,e=2.718···为自然对数的底数.
(1)讨论f(x)的单调性
(2)证明: 当x>1时,g(x)>0.
(3)确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立.
相同类型的题目有:

(I)求函数f(x)的单调递增区间;
(II)证明: 当x>1时,f(x)<x-1;
(III)确定实数k的所有可能取值,使得存在x0>1,当 x∈(1,x0)时,恒有f(x)>k(x-1).
3.(2015年福建高考卷理第20题)已知函数f(x)= ln(1+x),g(x)=kx(k∈R)
(I)证明: 当x>0时,f(x)<x;
(II)证明: 当k< 1时,存在 x0> 0,使得对任意x∈(0,x0),恒有f(x)>g(x);
(III)确定k的所有可能取值,使得存在t>0,对任意的x∈(0,t),恒有|f(x)-g(x)|<x2.
4.(15年新课标2理科21题)设函数f(x)=emx+x2-mx.
(1̉)证明: f(x)在(-∞,0)单调递减,在(0,+∞)单调递增;
(II)若对于任意x1,x2∈[-1,1],都有|f(x1)-f(x2)|≤e-1,求m的取值范围.
在解此类题目中,求解以逐段筛选法为主,辅之以构造函数、分离参变量等策略,用所学知识创造性地解决问题.同一类型的题目高频率地作为高考压轴题目出现,一方面说明这类题目有较好的区分度,另一方面也说明中学教学对此类问题研究不够,这也要求再高三复习教学中要善于总结逐段筛选法的一般思维方式.
当然,含参恒成立问题的题型和解题策略远不止这些,比如还有一次函数求解型,确定主元法,数形结合法,观察、证明、猜想等方法.而在解题中,解题方法常是交叉使用的,且解法并不唯一.
恒成立问题对学生思维能力的要求远远高于对知识的理解与一般意义上的运用,它是一种用于检测学生数学素质和思维能力的好载体,因此,含参恒成立问题深受命题者的青睐,它必将继续成为今后数学高考的一个热点,并且其命题背景还会更丰富.G·波利亚在《数学的发现》中曾说: “数学的技能比知识更重要.”因此,教师在复习过程中更要着重阐述分析问题和解决问题的一般规律和解题策略,从而让复习更有效.
[1]朱永江.基于高中数学的恒成立问题分析[J].开封教育学院学报, 2015,(3): 230-231
[2]赵忠平.年年“题”不同岁岁“法”相似——高考全国卷不等式恒成立成立求参数范围问题的解法分析[J].教学与管理,2012,(1): 72-73
[3]宋国清.谈不等式恒成立问题的基本类型和常见解法[J].数学教研, 2013,(19): 42-43
[4]杨洁.新课标中函数恒成立问题的解法[J].凯里学院学报,2014, (12): 171-173
