经验性最佳线性无偏预测(eBLUP)在油菜区域试验品种评价的效果
2017-03-16任长宏格桑曲珍胡希远
任长宏格桑曲珍胡希远
1西北农林科技大学农学院, 陕西杨凌712100;2西藏自治区康马县农牧综合服务中心, 西藏康马857500;3西藏自治区林木科学研究院, 西藏拉萨850000
经验性最佳线性无偏预测(eBLUP)在油菜区域试验品种评价的效果
任长宏1,2格桑曲珍1,3胡希远1,*
1西北农林科技大学农学院, 陕西杨凌712100;2西藏自治区康马县农牧综合服务中心, 西藏康马857500;3西藏自治区林木科学研究院, 西藏拉萨850000
线性混合模型最佳线性无偏预测(BLUP)不仅适用于数据不平衡和误差方差异质试验的分析, 而且对随机效应的排序会更准确。在实际试验分析中由于真实方差参数值未知而采用估计值时, BLUP转变为所谓经验性 BLUP (eBLUP)。为了探讨eBLUP在作物区域试验品种评价的效果, 本文以我国2012—2014年长江流域油菜区域试验12套产量资料为例, 对eBLUP在品种主效应和特定环境中效应的估计、排序及差异比较t测验等方面与方差分析综合比较。结果表明, 对品种主效应, eBLUP与方差分析算术平均值仅有较小差异, 品种排序在eBLUP与算术平均值法相同; 对特定环境中品种效应, eBLUP与算术平均值法有较大差异, 品种排序在eBLUP较算术平均值法更准确; 用Kenward-Roger法估算基于 eBLUP的效应差异 t测验的自由度, 无论对品种主效应还是对特定环境中品种效应, eBLUP和方差分析有着相近的显著性(α = 0.05)测验效果。
油菜试验; eBLUP; 品种评价; Kenward-Roger法
相比方差分析和一般线性模型等传统分析法,线性混合模型分析具有诸多优点, 包括可容易地处理不平衡(即由于数据缺失或设计本身造成的试验各处理重复数不相等)试验数据, 可分析误差方差异质(如, 不完全区组设计、误差方差存在异质性和空间相关)的试验数据, 对固定效应采用最佳线性无偏估计(BLUE), 而对随机效应采用最佳线性无偏预测(BLUP)[1-2]。BLUP的优点是, 能够利用方差参数提供的信息减小试验误差对效应排序的影响, 从而使效应排序比利用BLUE和算术平均值(采用算术平均值进行估计)的效应排序更准确[1,3-6]。因此, 近年来不断有学者建议在作物品种试验分析中将品种、环境和品种-环境互作效应三者之一或全部看作随机效应, 并采用线性混合模型BLUP进行评价。
我国作物品种区域试验(简称区试)传统上一般把品种、环境以及品种-环境互作效应均看作固定效应进行联合方差分析。近几年来, 则大多将环境(或称为地点)看作随机效应进行分析(见国家级油菜、玉米和小麦等区试报告)。将环境看作随机效应分析的优点在于可使关于品种评价的结论适用于更广的环境总体——包括试验和未试验的环境, 但区试数据的分析目前仍沿用方差分析法。该方法对只含有固定效应、数据平衡(所有处理重复数相等且无数据缺失)和误差方差同质的数据的分析是简单而准确的,但对不满足这些条件的试验数据的分析, 特别是关于品种效应的排序不一定是最佳的。线性混合模型及其BLUP为可替代的重要方法之一。
在实际试验分析中, 由于所研究效应的方差参数值, 例如作物多环境试验中品种主效应和品种-环境互作效应的方差参数值未知, 进行该效应的BLUP时只能利用由试验样本数据估计的方差值。采用方差参数估计值时, BLUP就转变为所谓的经验性 BLUP, 通常表示为 eBLUP[7]。eBLUP是否会如BLUP那样比其他方法对效应排序更准确, 则与所涉及的试验和效应有关, 或者说与方差参数估计的准确性有关。只有对方差参数估计足够准确的试验或效应, eBLUP才会表现出比其他方法对效应排序更准确的优势[7-8]。eBLUP在试验效应评价中还存在一个问题: 虽然 eBLUP有“无偏”(unbiased)的特性,但其含义不同于BLUE对每一水平下效应参数估计的无偏, 而是对效应总体参数估计的无偏, 对两水平间效应差值的估计通常是有偏的[1,8]。依据eBLUP得到的关于效应差值的 t统计量不同于方差分析中的 t统计量具有确定的统计分布, 而只能看作近似服从 t分布[1]。因此一般认为, 即使可利用 eBLUP对效应进行更准确的排序, 但基于eBLUP进行的效应差异显著性统计测验未必可靠。Forkman和Piepho[9]近期通过对单一环境随机区组设计试验的模拟研究指出, eBLUP虽然对效应差异估计有偏,但其在效应差异估计的均方误(MSE, 等于估计偏差的平方与误差方差之和)一般不超过方差分析估计的均方误。在基于eBLUP的效应差异t测验中采用Satterthwaite[10]或Kenward和Roger[11-12]法估算自由度, eBLUP可以达到和方差分析相近的效应差异显著性t测验结果。
本文的目的就是通过对我国近年油菜品种多环境试验取得的多套实际数据的分析, 比较线性混合模型eBLUP相对方差分析在品种效应估计、排序和差异显著性测验等方面的差异状况及其准确性, 为我国油菜以及其他作物区试分析中品种效应评价方法的合理选用提供参考。
1 材料与方法
1.1 数据来源
本文所分析资料为2012—2014年长江流域油菜(Brassica napus L.)国家区试产量数据。该区域每年有4组区试, 3年共12组(表1)。各组试验的环境部分相同, 各组试验的品种除对照外完全不同。所有环境中采用随机完全区组设计, 重复 3次。小区面积12 m2, 种植密度28万株 hm–2, 产量为每小区籽粒产量千克数。

表1 2012–2014年各组油菜区试中的品种数和环境数Table 1 Number of varieties and locations of multi-location trials for rape in 2012–2014
1.2 分析方法
所有试验分别利用SAS系统中PROC ANOVA和 PROC MIXED程序进行方差分析和线性混合模型eBLUP分析, 即在线性混合模型分析中将品种、环境及二者的互作均看作随机效应。随机效应方差参数采用限制性极大似然法(REML)估计, 随机效应eBLUP采用SAS PROC MIXED中的“ESTIMAT”语句进行编程予以实现, 基于eBLUP效应差异显著性t测验的自由度采用Kenward和Roger法估算, 即利用PROC MIXED进行数据分析时, 在MODEL语句中增加“DDFM=kenwardroger”。
2 结果与分析
2.1 品种效应估计与排序
相对方差分析中算术平均值, eBLUP具有向总体平均值“收缩”的趋势, 品种效应估计值在 eBLUP和方差分析间存在一定的差异。本文所分析全部试验中, 品种效应估计值在eBLUP和方差分析间也存在一定差异(数据略), 该差异在品种主效应和特定环境中效应的表现程度不同, 在品种主效应差异较小, 为–6.20%~4.48%, 在特定环境中品种效应差异较大, 为–9.4%~8.6%。对品种主效应 (表2), eBLUP和方差分析的排序在所有试验完全一致, 但对特定环境中品种效应的排序二者之间则出现了不同(表 3和表4)。以2012年第2组试验为例(表3), 12个试点中有11个试点(表3中有黑体数字出现的试点)品种排序在方差分析和 eBLUP之间存在着明显差异,差异程度随试点变化而不同, 例如在第 2试点只有品种4和品种12的排序在2种方法间发生了颠倒,但在第12试点则有9个品种的排序在两方法间发生了变化, 而且一些品种排序变化的间距也较大。在其余的11个试验中, 方差分析和eBLUP对特定环境中品种效应排序不一致的现象也有不同程度的表现,二者对特定环境中品种效应排序有差异的试点数占到试点总数的33.3% (2012年第1组试验12个试点中有4个不同)到100.0% (2013年第3组试验10个试点全部不同) (表4)。
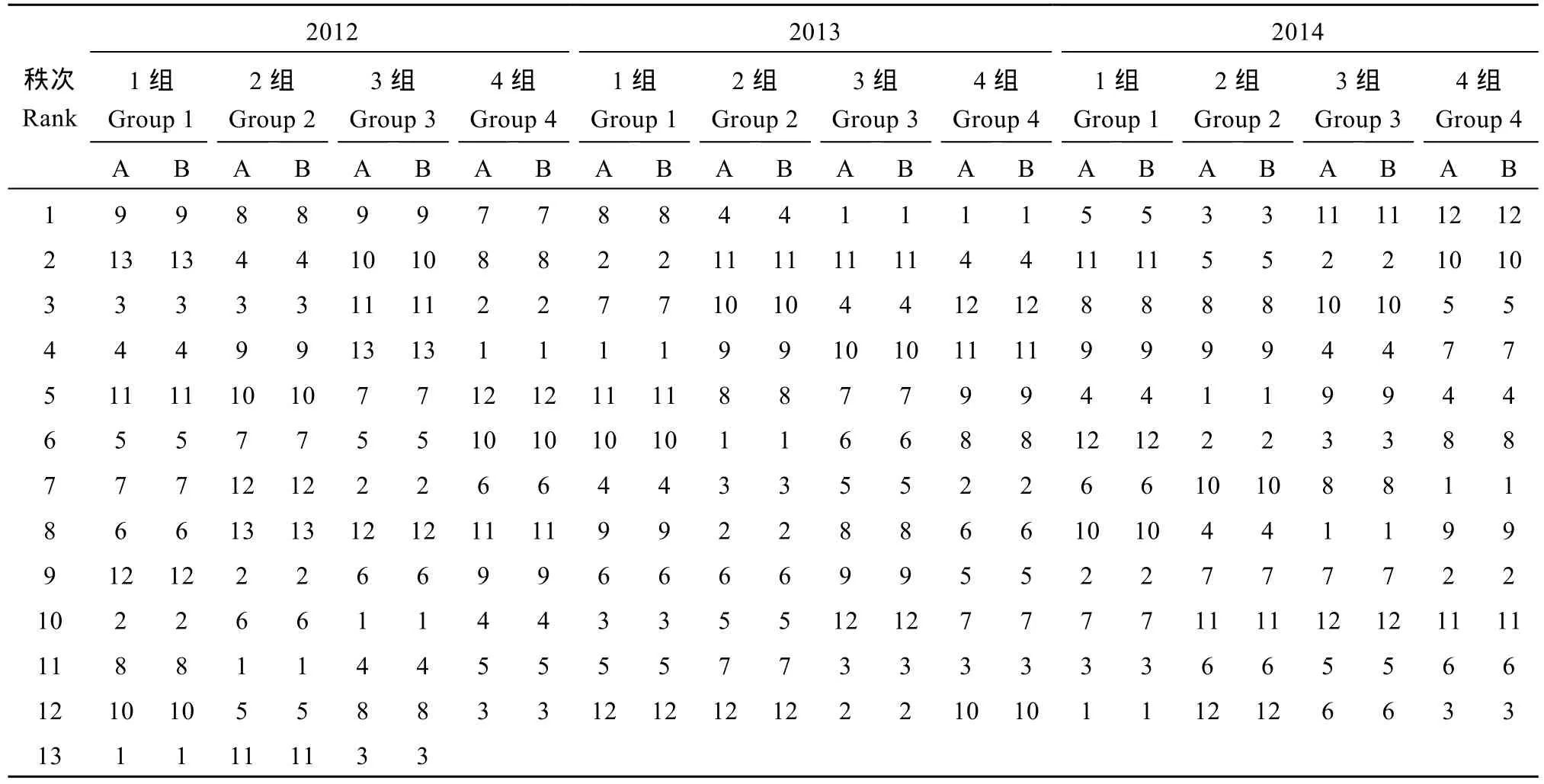
表2 各组油菜区试中利用方差分析(A)和eBLUP(B)对产量主效应排序的结果Table 2 Yield ranking of variety main effects using ANOVA (A) and eBLUP (B) for rape trials
2.2 效应差异t测验
品种产量t测验差异显著(α = 0.05)的品种对数在方差分析和eBLUP间的差异情况如表5和表6所示。从品种主效应测验的结果(表5)来看, 相比方差分析, eBLUP中产量差异显著的品种对数少0~7对,所有试验平均少 3.8对。从各试点中品种效应测验结果(表6)来看, 产量效应差异显著的品种对数在方差分析和eBLUP之间相差不超过±5对, 所有试点平均差异则更小, 未超过–1.2~1.0对。一方面, 相对各试验中可比较的品种总对数66 (品种数为12的试验)和78 (品种数为13的试验), 该差异数不是很大; 另一方面, 进一步比较分析也可知, 那些在方差分析和 eBLUP间形成差异显著性测验结果不同的品种,多数是因为其效应差异测验的概率值接近显著性水平0.05这个临界值, 微小的概率值变化就会导致效应差异显著或不显著的不同定性结论所致, 而效应差异测验的概率在方差分析和eBLUP间的差值本身多数并不大。这说明, 无论对品种主效应还是对特定环境中品种效应, 基于eBLUP和方差分析有着相近的差异显著性测验结果。
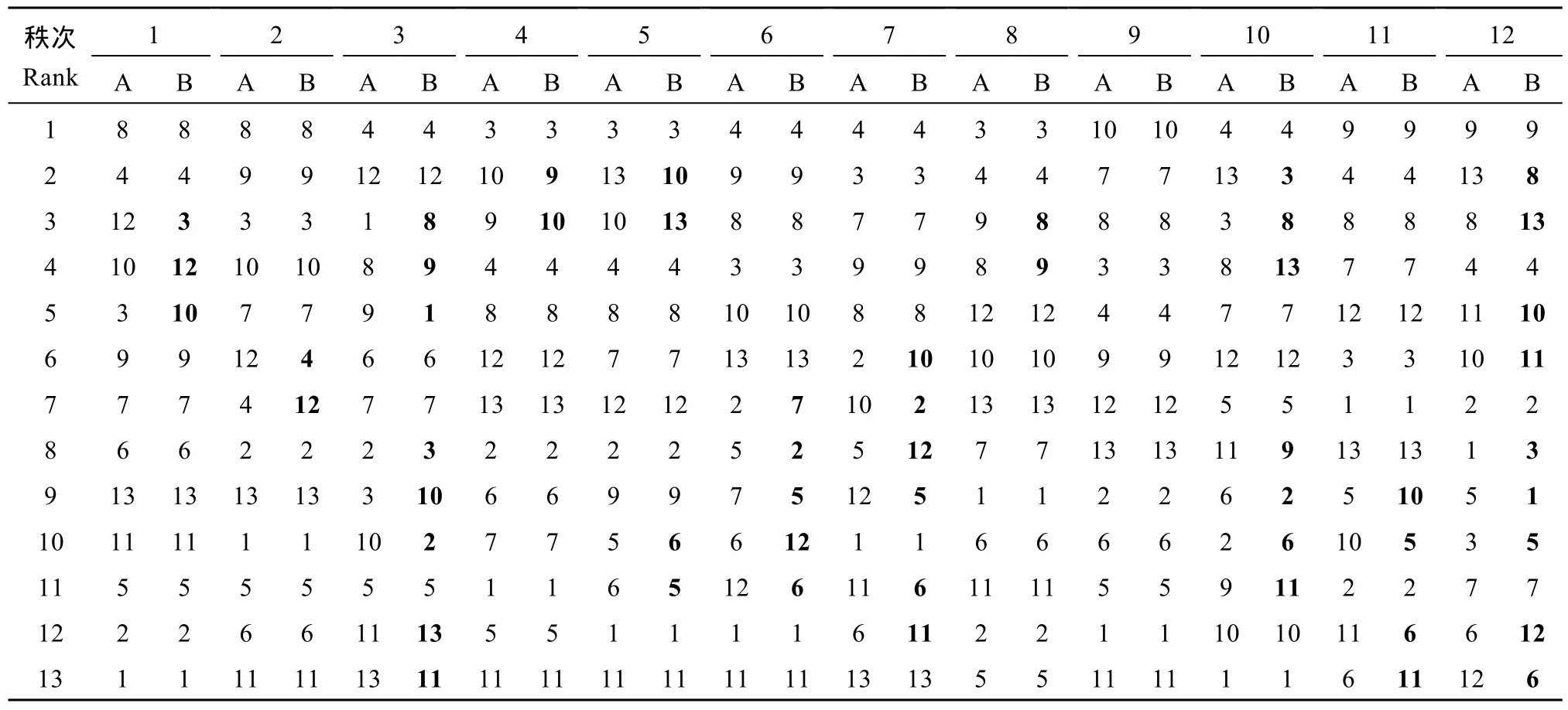
表3 2012年第2组油菜试验中利用方差分析(A)和eBLUP(B)对不同试点(1~12)中品种(1~13)产量效应排序的结果Table 3 Yield ranking of variety location-specific effects at different locations (1–12) for the trial of group 2 in 2012 using ANOVA (A) and eBLUP (B)

表4 各试验中品种产量排序在方差分析和eBLUP有所不同的试点数Table 4 Number of locations the yield rank of genotype was not all identical between ANOVA and eBLUP for the trials

表5 各试验中品种主效应差异在方差分析(ANOVA)和eBLUP达显著(α = 0.05)的品种对数及其差值Table 5 The variety pairs with significant (α = 0.05) difference in ANOVA and eBLUP and their discrepancy
2.3 eBLUP对品种效应排序的准确性
由于特定环境中品种效应的排序在方差分析和eBLUP有所不同, 这里对二者的相对准确性予以验证。根据文献[13], 对不同方法在特定环境品种效应排序的相对准确性可利用品种效应估计值在不同环境的Pearson’s相关系数予以评判。虽然该相关系数不仅与特定环境中品种效应排序的准确性有关, 而且还与品种-环境互作效应的大小有关, 但其互作效应并不因分析法不同而改变, 对该相关系数在各种方法中的影响是相同的。所以可利用该相关系数评判不同方法对特定环境中品种效应排序的相对准确性, 即相关系数越大, 相应方法对品种效应排序越准确。表7中具有较大Pearson’s相关系数数目的比例和表 8中 Pearson’s相关系数的平均值都可表明, eBLUP对特定环境中品种效应排序的准确性高于方差分析算术平均值法。
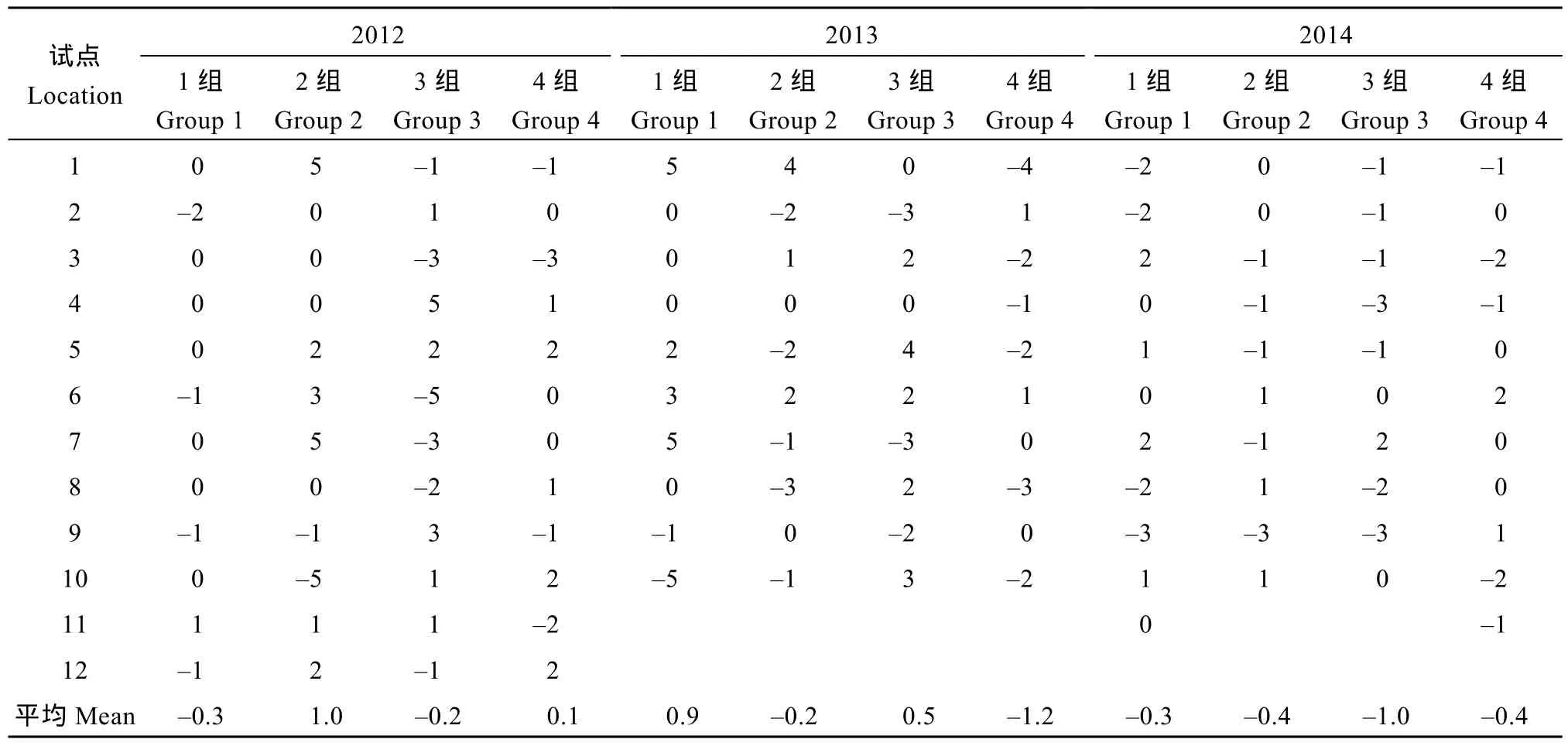
表6 各试验不同试点中品种效应差异达显著(α = 0.05)的品种对数在方差分析和eBLUP间的差值Table 6 Discrepancy of significant (α = 0.05) variety pairs between ANOVA and eBLUP for difference test on location-genotype effects in trials

表7 特定环境中品种效应Pearson’s相关系数在eBLUP比在方差分析大的数目百分比Table 7 Number percentage of higher Pearson’s correlation in eBLUP than that in ANOVA between locations and varieties

表8 特定环境中品种效应Pearson相关系数在方差分析(ANOVA)和eBLUP中的平均值Table 8 Average Pearson’s correlation in eBLUP and ANOVA between locations and varieties
3 讨论
BLUP为线性混合模型中随机效应的标准估计方法, BLUP或eBLUP一开始只用于动物育种值的估计, 而后逐渐广泛地应用于许多研究领域[3]。在植物遗传学领域, 线性混合模型分析则主要用于遗传或非遗传方差组分的估计[8,14-15]。如今, 一些国家已将线性混合模型eBLUP用于作物试验的品种评价与选择[1,16-19], 特别是在澳大利亚已将eBLUP作为作物(包括单环境和多环境)试验品种评价的标准方法[19]。
本文结果表明, 对我国目前油菜区域试验设计状况, 即品种数和试点数都在十几个左右, 所有试点用随机区组设计, 重复3次, 利用eBLUP进行品种排序与选优是可行的。对品种主效应排序, eBLUP可达到与方差分析算术平均法相同的效果; 对特定环境中品种效应的排序, 前者比后者更准确。eBLUP排序准确性在品种主效应和特殊效应间呈现的这种差别, 是由试验中品种主效应水平数和品种-环境互作效应水平数的不同而导致的, 即主效应水平数(=试验品种数)少, 其效应方差估计准确性较低,使 eBLUP显现不出优势; 品种-环境互作效应水平数(=品种数×环境数)多, 其效应方差估计准确性较高, 足以使eBLUP呈现出类似BLUP的优势。关于特定环境品种效应 eBLUP较算术平均值的准确性,张群远等[20]利用交叉验证取得的增益倍数(Gainfactor, GF)对棉花区域试验数据得到了类似的结论。
本文还表明, 在基于eBLUP的效应差异t测验中利用 Kenward-Roger法进行自由度估算, 无论对品种主效应还是对特定环境中的品种效应, eBLUP t测验和方差分析t测验有着相近的显著性测验结果。这样就可以克服只能利用eBLUP进行品种效应估计与排序, 而不能利用其进行差异显著性测验的限制。但需要说明的是, 本文只是基于实际几个试验的分析取得的初步直观研究结果, 关于eBLUP在其他试验设计, 尤其是在不同品种数目的试验中对品种评价的效果, 以及更具说服力的结论, 还有待进一步的具体分析和模拟研究。
值得一提的是, 在区试分析中首先应当利用 F测验, 看数据中有无较大的品种主效应和品种-环境互作效应, 并由此决定利用试验数据对不同品种进一步的比较与评价。这一过程, 在线性混合模型eBLUP和方差分析均是必须的。由于对平衡数据,效应F测验的结果在线性混合模型和方差分析是一致的[8], 而且本文的主要目的是探讨品种效应排序与两两比较t测验在线性混合模型eBLUP和方差分析的差异状况, 所以文中省去了F测验的过程和结果。
长期以来, 固定效应模型(也称一般线性模型, ordinary linear model)和基于固定效应模型的方差分析, 是教科书中经典的试验分析方法, 为人们普遍熟知和广泛应用。因此, 对实际试验分析者, 很有必要明确几个问题: 固定效应模型不好, 还能不能用?混合效应模型好, 好的标准是什么?有多好?依据文献和作者的认知给予如下说明。
尽管混合效应模型较固定效应模型在理论上有诸多优点, 但由于其涉及的数学运算较复杂, 一般只能借助计算机程序才可实现。所以, 关于混合效应模型在各领域应用的大量研究报道是在近年一些统计软件(例如SAS和SPSS)中开发了混合效应模型分析的功能后, 使混合效应模型分析过程变得和方差分析过程近乎一样容易才出现的。固定效应模型可看作是混合效应模型一定条件下的特例, 混合效应模型是固定效应模型的推广。具体来说: 第一, 凡能用固定效应模型分析(即符合固定效应模型或方差分析条件, 例如试验误差同质和独立、数据平衡)的试验数据, 也可利用混合效应模型分析, 且在效应估计和效应差异显著性测验等方面与前者等效;对不符合固定效应模型和方差分析条件的试验数据,利用混合效应模型分析, 在效应估计和效应差异显著性测验等方面会更准确[21]。这是由它们各自对固定效应估计所采用的方法决定的: 固定效应模型分析和方差分析分别用最小二乘法和算术平均值法,而混合效应模型采用BLUE。第二, 如果试验分析的目的是要为服务地区选出适宜的品种, 那么混合效应模型BLUP比固定效应模型和方差分析可能会更可靠, 这是由BLUP的特性决定的, 即BLUP能够将方差参数所提供的关于效应分布的信息用于效应值的预测。有研究者指出[3], 实际上只有当试验品种数超过20个时, BLUP在品种优选方面较固定效应模型更可靠的优势才会显现出来。本文结果与该观点相一致。因此, 固定效应模型在区域试验通常是可用和有效的, 只是在试验数据特性偏离方差分析的条件和品种数相当多时, 其在品种效应测验和优选方面不及混合效应模型分析结果可靠。
还值得提及的是, 在区域试验分析中有时还要借助于双标图技术进行品种生态区(Mega-Environment)的划分[22], 这样才能充分挖掘试验信息。本文没有触及这一点, 而是接受了全部试验属于同一品种生态区的假设。但从表 8中所示年内试验间较小的相关系数可以推断, 这个假设的可靠性及其对分析结果的影响还有待进一步探讨。关于双标图技术在区域试验分析的应用, 读者可参阅相关文献, 特别是原创作者严威凯的相关文献。
4 结论
就我国近年油菜品种区域试验设计状况, 对品种主效应, eBLUP与方差分析算术平均值仅有较小差异, 品种排序在eBLUP与算术平均值法相同; 对特定环境中品种效应, eBLUP与算术平均值法有较大差异, 品种排序在eBLUP较算术平均值法更准确;用Kenward-Roger法估算基于eBLUP的效应差异t测验的自由度, 无论对品种主效应还是对特定环境中品种效应, eBLUP和方差分析有着相近的显著性(α = 0.05)测验效果。
[1] Smith A B, Cullis B R, Thompson R. The analysis of crop cultivar breeding and evaluation trials: an overview of current mixed model approaches. J Agric Sci, 2005, 43: 449–462
[2] Searle S R, Casella G, McCulloch C E. Variance Components. New York: John Wiley & Sons, Inc., 1992
[3] Stroup W W, Mulitze D K. Nearest neighbor adjusted best linear unbiased prediction. Am Stat, 1991, 45: 194–200
[4] Real D, Gordon I L, Hodgson J. Genetic advance estimates for red clover (Trifolium pratense) grown under spaced plant and sward conditions. J Agric Sci, 2000, 135: 11–17
[5] Smith A B, Lim P, Cullis B R. The design and analysis of multi-phase plant breeding experiments. J Agric Sci, 2006, 144: 393–409
[6] Sarker A, Singh M, Erskine W. Efficiency of spatial methods in yield trials in lentil (Lens culinaris ssp. culinaris). J Agric Sci, 2001, 137: 427–438
[7] Piepho H P. Empirical best linear unbiased prediction in cultivar trials using factor analytic variance-covariance structures. Theor Appl Genet, 1998, 97: 195–201
[8] Piepho H P, Möhring J, Melchinger A E, Büchse A. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica, 2008, 161: 209–228
[9] Forkman J, Piepho H P. Performance of empirical BLUP and Bayesian prediction in small randomized complete block experiments. J Agric Sci, 2013, 151: 381–395
[10] Satterthwaite F E. An approximate distribution of estimates of variance components. Biometr Bull, 1946, 2: 110–114
[11] Kenward M G, Roger J H. Small sample inference for fixed effects from restricted maximum likelihood. Biometrics, 1997, 53: 983–997
[12] Kenward M G, Roger J H. An improved approximation to the precision of fixed effects from restricted maximum likelihood. Comput Stat Data Anal, 2009, 53: 2583–2595
[13] Müller B U, Kleinknecht K, Möhring J, Piepho H P. Comparison of spatial models for sugar beet and barley trials. Crop Sci, 2010, 50: 794–802
[14] 朱军. 线性模型分析原理. 北京: 科学出版社, 2000 Zhu J. Principles of Linear Model Analysis. Beijing: Science Press, 2000 (in Chinese)
[15] 翟虎渠. 应用数量遗传学. 北京: 中国农业出版社, 2001 Zhai H Q. Applied Quantitative Genetics. Beijing: China Agriculture Press, 2001 (in Chinese)
[16] Piepho H P, Möhring J. Best linear unbiased prediction of cultivar effects for subdivided target regions. Crop Sci, 2005, 45: 1151–1159
[17] Kleinknecht K, Möhring J, Singh K P, Zaidi P H, Atlin G N, Piepho H P. Comparison of the performance of best linear unbiased estimation and best linear unbiased prediction of genotype effects from zoned Indian maize data. Crop Sci, 2013, 53: 1384–1391
[18] Leiser W L, Rattunde H F, Piepho H P, Weltzien E, Diallo A, Melchinger A E, Parzies H K, Haussmann B I G. Selection strategy for sorghum targeting phosphorus limited environments in West Africa: analysis of multi-environment experiments. Crop Sci, 2012, 52: 2517–2527
[19] Smith A, Cullis B, Gilmour A. The analysis of crop variety evaluation data in Australia. Aust New Zealand J Stat, 2001, 43: 129–145
[20] 张群远, 孔繁玲. 作物品种区域试验中品种均值估计的模型和方法——算术平均值、加权最小二乘估值和BLUP的比较.作物学报, 2003, 29: 884–891 Zhang Q Y, Kong F L. Models and methods for estimating variety means in regional crop trials: comparisons of arithmetic mean, weighted least squares estimates and BLUPs. Acta Agron Sin, 2003, 29: 884–891 (in Chinese with English abstract)
[21] Littell R C, Milliken G A, Stroup W W, Wolfinger R D. SAS System for Mixed Models, 2nd edn. Inc. Cary, NC: SAS Institute, 2006
[22] 严威凯. 双标图分析在农作物品种多点试验中的应用. 作物学报, 2010, 36: 1805–1819 Yan W K. Optimal use of biplots in analysis of multi-location variety test data. Acta Agron Sin, 2010, 36: 1805–1819 (in Chinese with English abstract)
Performance of eBLUP in Variety Evaluation of Regional Rape Trials in China
REN Chang-Hong1,2, Gesangquzhen1,3, and HU Xi-Yuan1,*1College of Agronomy, Northwest A&F University, Yangling 712100, China;2Kangma Integrated Service Center for Agriculture and Animal Husbandry of Tibet Autonomous Region, Kangma 857500, China;3Institute of Forestry Seedling Science & Technique of Tibet Autonomous Region, Lhasa 850000, China
The mixed model and its best linear unbiased prediction (BLUP) are more suitable for analysis of the trails with unbalanced data and heterogeneous errors, and BLUP can provide more accurate ranking for random effects. In analysis of practical trials, the variance parameters are unknown and their estimates have to be used. In this case, the BLUP become empirical BLUP (eBLUP). To investigate the performance of eBLUP in variety valuation of regional crop trials in China, this paper compared estimates, ranking and t-test for both variety main effects and location-specific variety effects between using ANOVA and eBLUP based on 12 yield data sets from the rape variety evaluation trials of China from 2012–2014. The method of Kenward and Roger was used for approximating denominator degrees of freedom in t-test for effect difference comparison based on eBLUP. The results showed that in view of variety main effects, there was only small discrepancy between eBLUP and arithmetic mean of ANOVA, variety ranking was the same between them; in view of location-specific variety effects, there was large discrepancy between eBLUP and arithmetic mean, variety ranking was more accurate in eBLUP than arithmetic mean; in t-test for both variety main effects and location-specific variety effects, eBLUP and ANOVA provided similar variety pairs with significant (α = 0.05) difference.
Rape trial; eBLUP; Variety evaluation; Kenward-Roger method
10.3724/SP.J.1006.2017.00371
本研究由陕西省自然科学基金项目(2012JM3009)资助。
The study was supported by the Natural Science Foundation of Shaanxi Province of China (2012JM3009).
*通讯作者(Corresponding author): 胡希远, E-mail: xiyuanhu@aliyun.com, Tel: 13072926729
稿日期): 2016-04-20; Accepted(接受日期): 2016-09-18; Published online(
日期): 2016-09-28.
URL: http://www.cnki.net/kcms/detail/11.1809.S.20160928.0948.016.html
