地基对电液振动台性能的影响分析
2017-03-16郝岩研窦雪川杨志鹏
郝岩研,窦雪川,杨志鹏,李 红
(北京强度环境研究所,北京 100076)
【机械制造与检测技术】
地基对电液振动台性能的影响分析
郝岩研,窦雪川,杨志鹏,李 红
(北京强度环境研究所,北京 100076)
基于试验室现有的电液振动台,先后建立振动台以及振动台和安装地基组合体的数学模型。针对振动台地基的各项性能参数开展仿真对比并进行相关试验验证,分析地基各性能参数对振动台工作性能的影响。
地基;电液振动台;数学模型
电液振动台台面承载质量大,振幅大,频率低,结构本身不具备减振功能。当振动台液压缸产生一个向上的激振力时,液压缸体也会产生一个向下的力。该作用力需要施加于一个足够大的反作用质量块上,才能减小对台体的影响。因此,电液振动台需要专有的安装地基。
如果安装地基设计不当,不仅会对周围的建筑结构产生危害,而且会对电液振动台的自身性能包括振幅、速度、加速度、波形失真等多个方面造成不良影响[1-3],导致振动台难以精确控制。
本文对电液振动台及其安装地基建立数学模型,分析安装地基对电液振动台性能的影响。
1 数学模型
电液振动台内环采用位移控制,属于电液位置伺服系统。以典型单轴电液振动台为例进行建模,分析安装地基的影响。图1为电液振动台结构示意图。此振动台系统原理可由图2表示。
1.1 基本数学模型
如果不考虑安装地基对系统的影响,数学模型的建立主要包括伺服放大器、伺服阀、液压执行元件等几部分。
1) 伺服放大器的数学模型
ic/Δu=Ki
ic为伺服放大器输出信号值;Δu为输入指令信号u与反馈信号uf的差值,即Δu=u-uf;Ki为伺服放大器放大倍数。
2) 伺服阀的数学模型[4-5]
将伺服阀表示为振荡环节。
xv为伺服阀阀芯位移;Ks为伺服阀增益;Ts为伺服阀周期(时间常数);ξs为伺服阀相对阻尼系数。
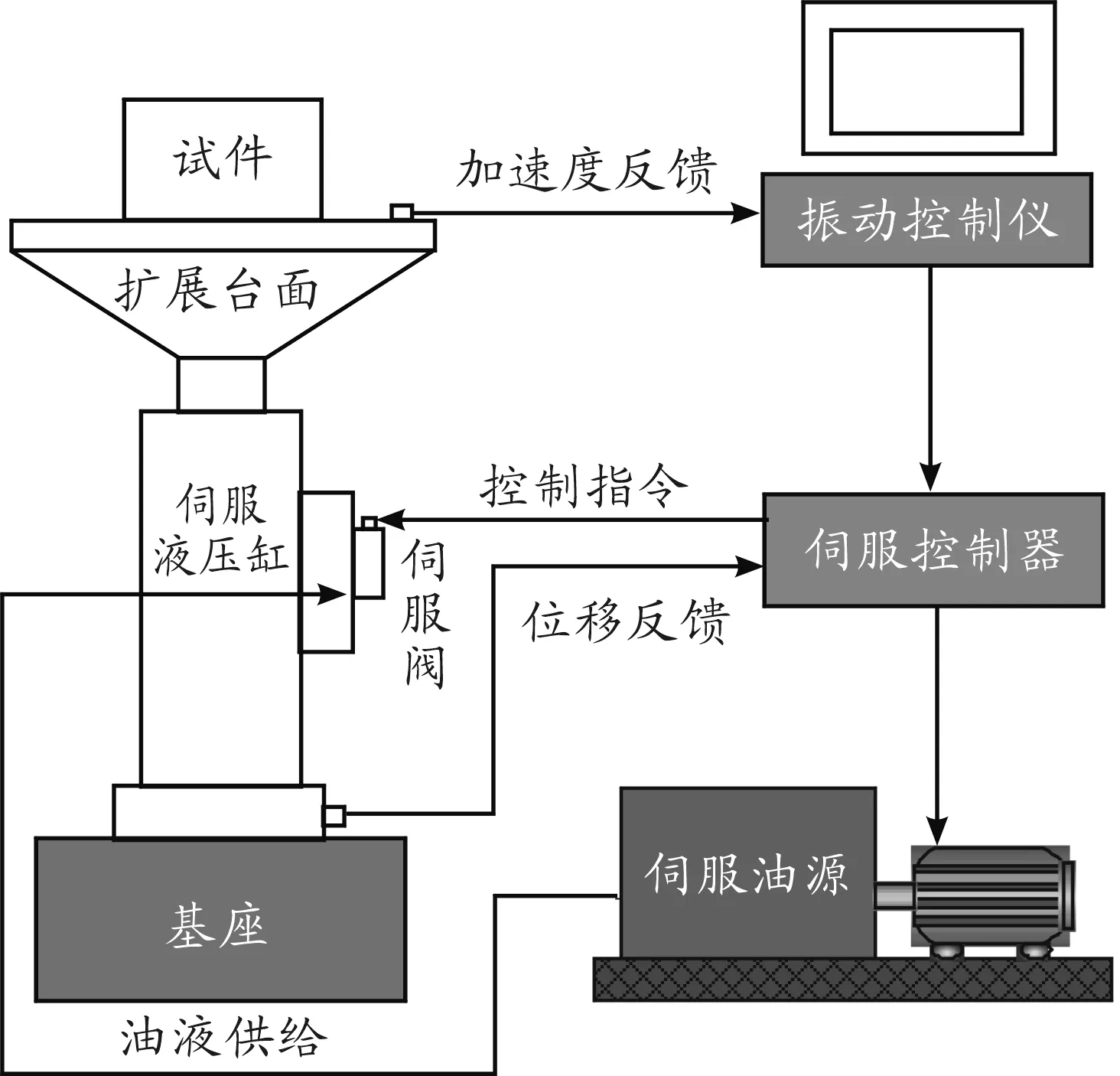
图1 电液振动台结构示意图
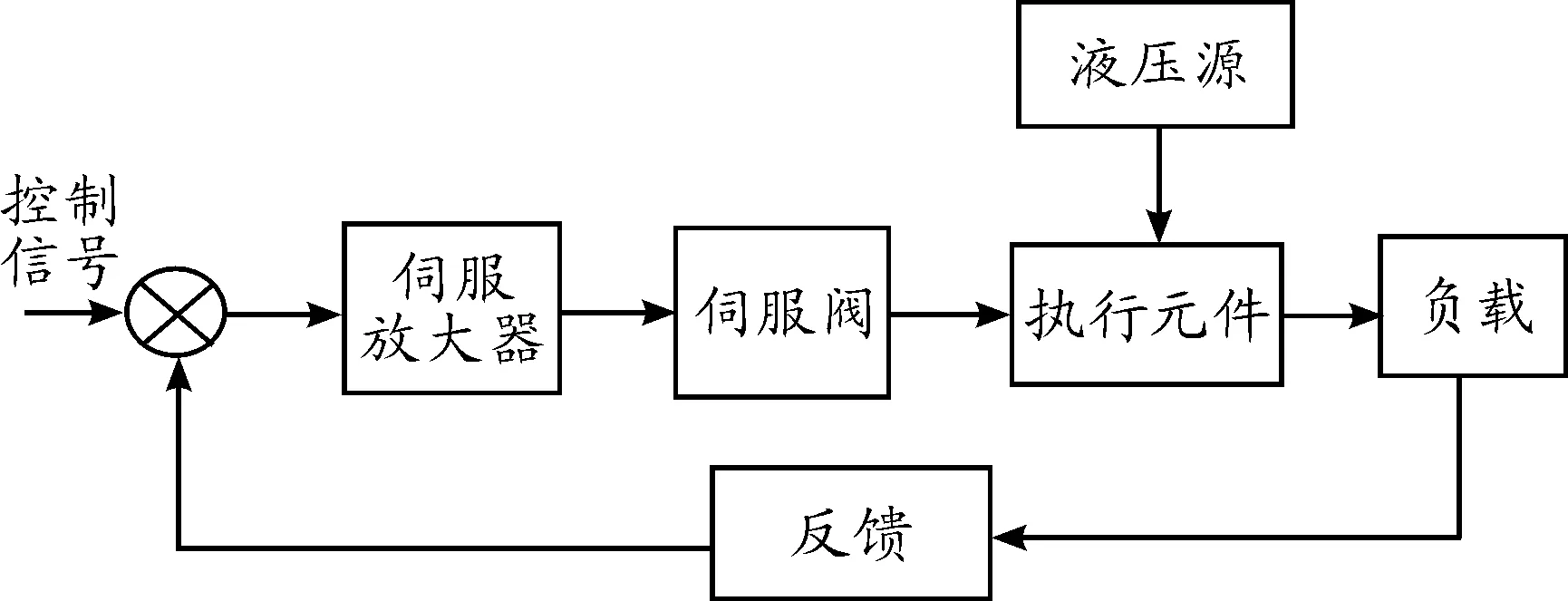
图2 电液振动台系统原理图
3) 液压执行元件的数学模型[6-10]
(1)线性化后的伺服阀流量方程
Qf=Kqxv-Kcpf
其中,
Qf为负载流量;Cv为滑阀节流窗口的节流系数;W为伺服阀的面积梯度;ps为油源压力;pf为负载压力;ρ为液压油密度。
(2)液压缸流量方程
At为液压缸的活塞面积;Vt为液压缸的有效容积;xt为液压缸的活塞位移;Ey为等效容积弹性模数;Csl为液压缸总泄露系数。
(3)液压缸负载力平衡方程
mt为运动部分折算到液压缸活塞上的总质量;Bt为液压缸活塞与负载运动的粘性阻尼系数。
将上述各等式进行拉氏变换之后,可以解出电液振动台的传递函数,电液振动台的基本数学模型如图3所示。

图3 电液振动台的基本数学模型
1.2 安装地基影响下的数学模型
当液压缸产生一个向上的激振力时,同时会有一个作用力施加于安装地基之上。对安装地基的受力状态进行建模,分析受力对其产生的影响。
1) 安装地基的负载力平衡方程
xd为台体及安装地基在反作用力下的位移量;md为台体及安装地基的等效质量;Bd为台体及安装地基的等效阻尼系数;Kd为安装地基的弹性系数。
2) 考虑安装地基对电液振动台造成影响的液压缸负载力平衡方程
x0为负载位移,x0=xt-xd。
根据上述分析,考虑安装地基对电液振动台的影响,电液振动台的数学模型可以表示如图4。

图4 安装地基影响下振动台的数学模型
2 安装地基影响分析
通过比较电液振动台在考虑安装地基的影响前和影响后的数学模型,可以看出安装地基的影响主要集中于后半部分。分别对图3和图4进行简化,简化的结果如图5和图6所示(其中Kcs=Kc+Csl),由此可分别得出系统的传递函数G(s)和G′(s)。

图5 简化后的基本数学模型
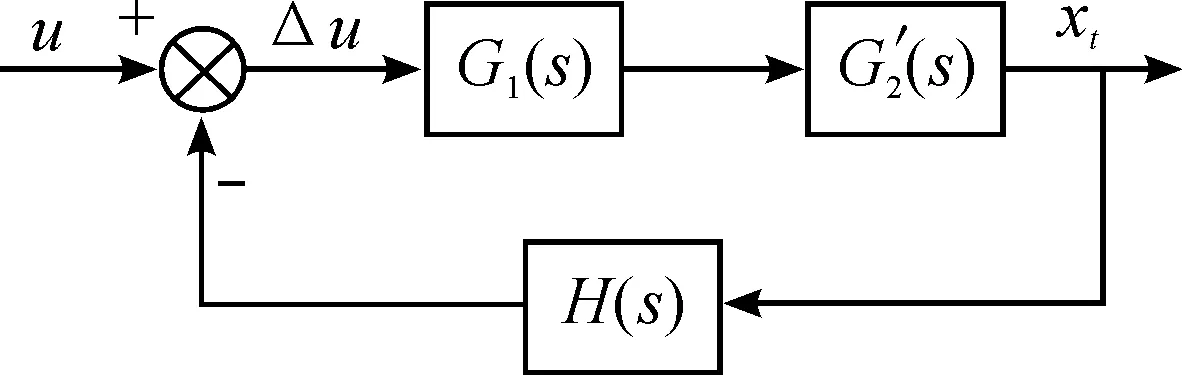
图6 简化后安装地基影响下的数学模型
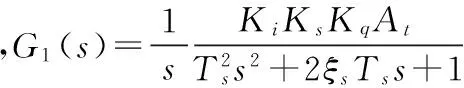
H(s)=Kf
对比G(s)和G′(s)可知,当md>>mt,且Bd>>Bt时,可将G′(s)简化为G(s),与考虑安装地基影响之前是完全一致的,重点考虑md和Bd的变化对系统造成的影响。
分别考虑md和Bd的影响,假设Bd>>Bt,此时,G2′(s)可简化为
其中,
由上式可以得出,At′>At,则
因此,md和mt之间的差距越小,G2a′(s)的固有频率越小,当md>>mt时,G2a′(s)的固有频率无限接近于G2(s)的固有频率。
假设md>>mt,考虑Bd的影响,此时G2′(s)可简化为
其中,
由上式可知,此时K′越小,G2b′(s)的固有频率越小,当md和Kd的数值较大时,Bd的数值也相应变大,K′变小。
3 仿真与试验
以试验室的18 t电液振动台及其安装地基为例,进行系统仿真和试验,18 t液压振动台的基本参数如表1所示。
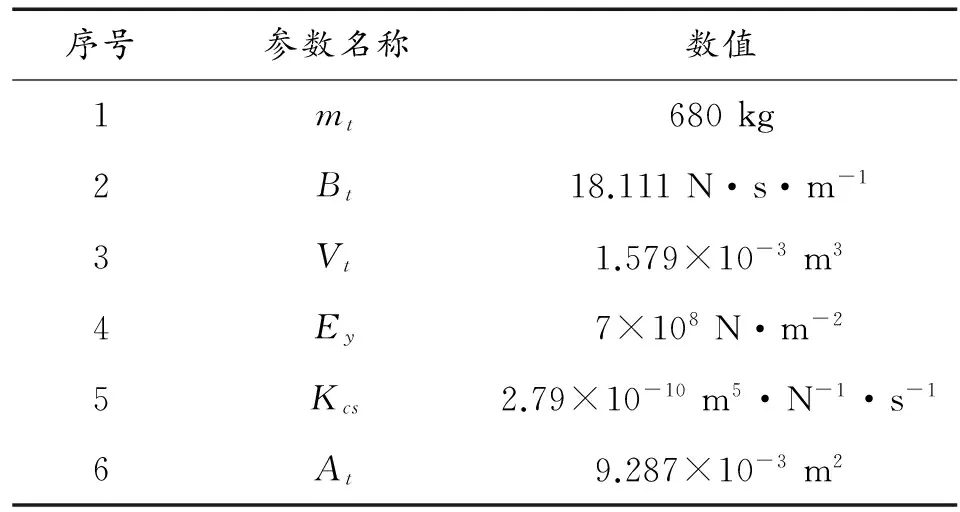
表1 振动台参数
试验室内有一块砂石地基,总质量为1 000 t,确定砂石地基的参数,md为1×106kg,Kd为5×107N·m-1。
将上述参数带入振动台的数学模型,进行仿真,可得系统开环和闭环传递函数bode图,分别如图7、图8和图9所示,图中三条曲线,实线、虚线和点划线分别对应地基质量为1 t、10 t和1 000 t时的曲线。
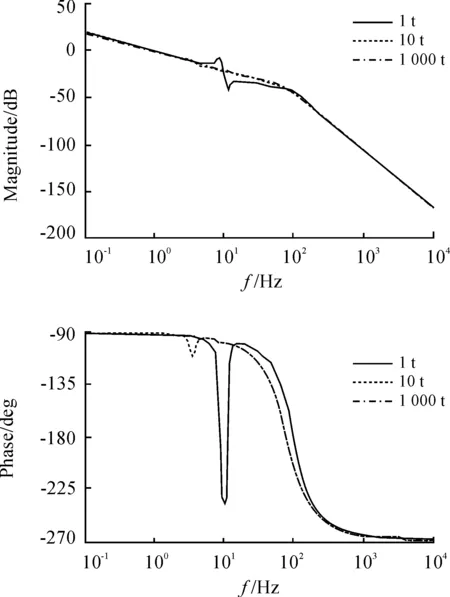
图7 系统开环传递函数bode图
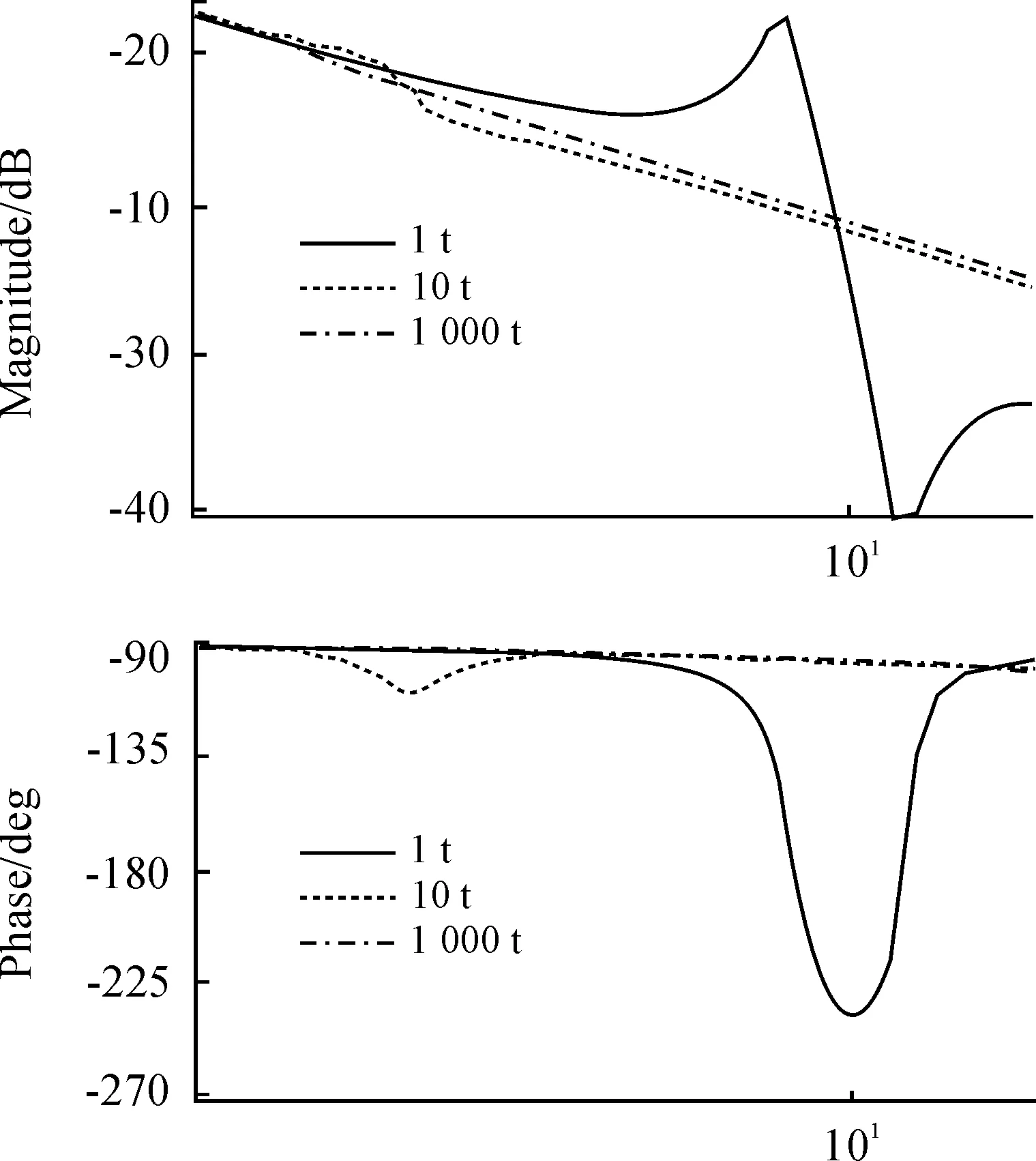
图8 系统开环传递函数bode图局部放大
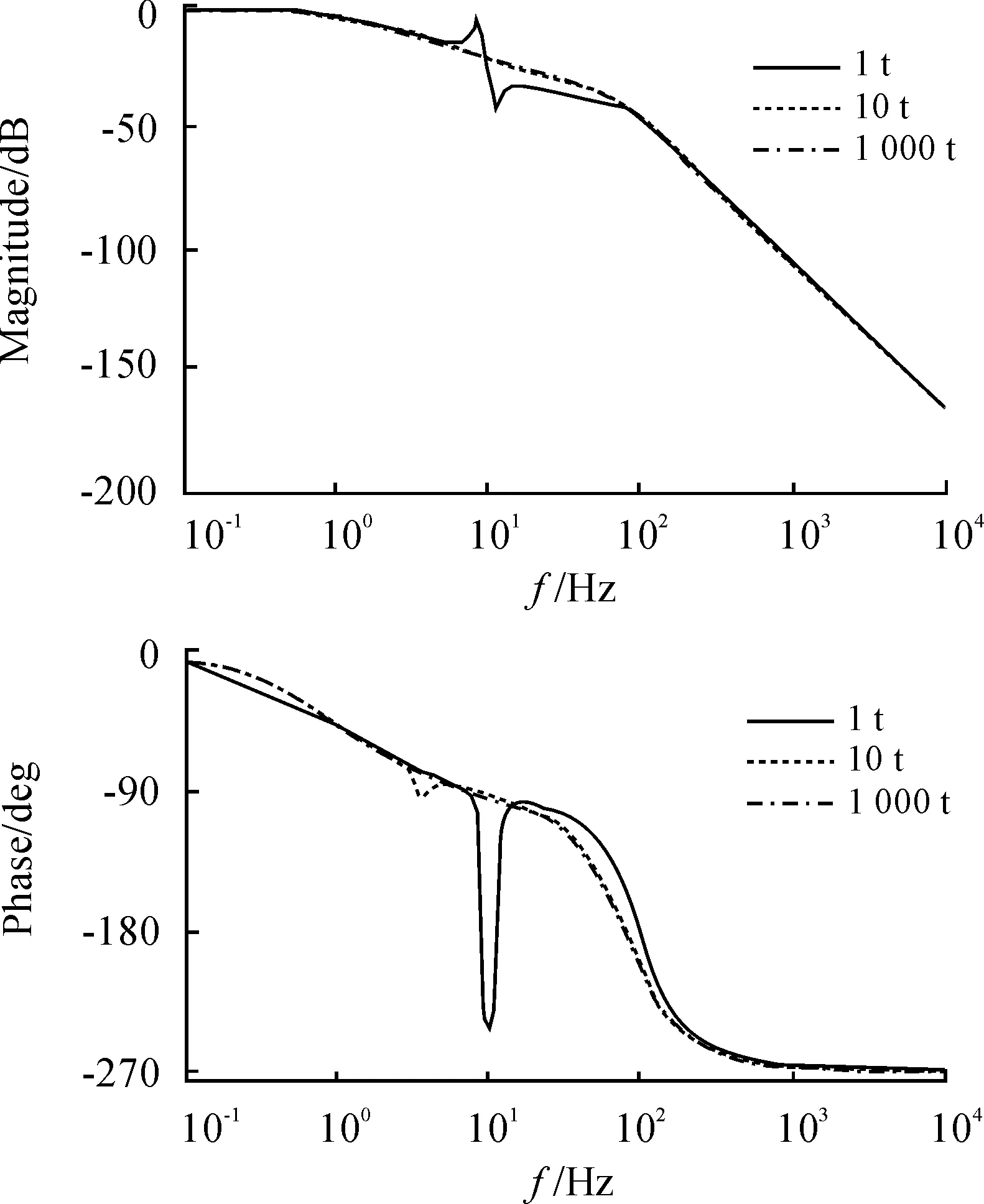
图9 系统闭环传递函数bode图
由图可以看出,随着地基质量的降低,系统谐振峰和反谐振峰的幅值变大,且逐渐向高频移动。虽然在谐振峰处,系统频率响应被提高,但受反谐振影响,反谐振峰附近区域的频率响应略有降低。在低频段,受谐振的影响,系统幅值裕度降低。
因此对于重点应用于低频段振动的电液振动台来说,地基质量越大,对系统频率响应越是有益。
采用试验室内的18 t电液振动台进行验证,试验结果如图10所示。图中虚线是电液振动台安装在1 000 t砂石地基上的幅频特性曲线,实线是以电液振动台的底座(重量不足10 t)作为地基进行试验时的幅频特性曲线。
由图10可以看出,大地基时系统谐振峰出现在频率较低位置,小地基时系统谐振峰频率提高,且在局部范围内因为反谐振峰影响,幅值下降较快,与系统仿真曲线具备相似的特征。
4 结论
1) 地基的质量是影响电液振动台性能的重要因素。地基质量过小,会导致谐振峰与反谐振峰的幅值变大,频带变宽。在设计电液振动台时,需要设计合适的地基,保证电液振动台具有一定的动态性能。
2) 本文主要研究和验证了地基质量过小对系统带来的不利影响,并未验证地基质量增至多大量级对系统的影响可以忽略不计,后续可做相关的研究和验证,为电液振动台的地基设计提供理论依据,既不浪费资源,又能具有良好的性能。
[1] 方子明,黄福云,陈宝春,等.福州大学地震模拟振动台三台阵基础设计与施工研究[J].福州大学学报(自然科学版),2013,41(4):807-812.
[2] 王磊,丁海平.地震模拟振动台基础动力反应的比较研究[J].常州工学院学报,2013,26(2):28-32.
[3] 尹谦钧,侯杰,邱法维.地震模拟振动台的基础设计研究[J].工程抗震与加固改造,2009,31(4):40-44.
[4] 李振宝,唐贞云,黄浩华,等.伺服阀性能改善及其在地震模拟振动台中的应用[J].武汉理工大学学报,2010,32(9):194-198.
[5] LIU Changhai,JIANG Hongzhou.A seventh-order model for dynamic response of an electro-hydraulic servo valve[J].Chinese Journal of Aeronautics,2014,27(6):1605-1611.
[6] 王燕华,程文瀼.地震模拟振动台运动控制性能分析[J].振动与冲击,2010,129(2):100-106.
[7] 张培,许宏光,郑大可,等.新型电液负载模拟器建模及仿真研究[J].液压与气动,2015(2):98-102.
[8] 李少年,冀宏,魏列江,等.一种阀控缸非线性特性研究[J].液压与气动,2014(2):53-55.
[9] 延皓,李长春,陈策.电液伺服系统综合负载模拟器仿真与试验研究[J].液压与气动,2013(3):49-53.
[10]裴忠才,王占林,王立国.电液负载仿真台的理论分析[J].北京航空航天大学学报,2000,26(6):660-662.
(责任编辑 唐定国)
Influence Analysis of Foundation to Performance of Hydraulic Vibrator
HAO Yan-yan,DOU Xue-chuan,YANG Zhi-peng,LI Hong
(Beijing Institute of Structure and Environment Engineering, Beijing 100076, China)
Based on the shaker in the laboratory, the mathematical model of the shaker was established, and the mathematical model of the shaker and its foundation were established. The simulations and tests were carried out for parameters of the foundation used by the shaker, and the effects of foundation parameters to the shaker are analyzed.
mounting foundation;hydraulic vibrator;mathematical model
2016-09-22;
2016-10-20
郝岩研(1985—),男,硕士,工程师,主要从事液压系统设计集成研究,E-mail:13661122823@139.com。
10.11809/scbgxb2017.02.031
郝岩研,窦雪川,杨志鹏,等.地基对电液振动台性能的影响分析[J].兵器装备工程学报,2017(2):135-139.
format:HAO Yan-yan,DOU Xue-chuan,YANG Zhi-peng,et al.Influence Analysis of Foundation to Performance of Hydraulic Vibrator[J].Journal of Ordnance Equipment Engineering,2017(2):135-139.
TP13
A
2096-2304(2017)02-0135-05
