基于动态RBF网络辨识和模糊控制的弹道落点预测导引研究

冯耀暄，薄学纲

(1.中北大学机电工程学院，太原，030051; 2.江苏永丰机械有限责任公司，南京 210014)

【信息科学与控制工程】

基于动态RBF网络辨识和模糊控制的弹道落点预测导引研究

冯耀暄1，薄学纲2

(1.中北大学机电工程学院，太原，030051; 2.江苏永丰机械有限责任公司，南京 210014)

针对目前远程弹道修正火箭弹中，滤波外推落点预测导引法存在导引系数确定难、导引精度低、自适应性与鲁棒性差的问题，提出了一种基于动态RBF神经网络在线辨识与带自调整因子模糊控制相结合的落点预测导引律。具体在传统滤波外推落点预测导引法的基础上，将预测落点偏差与偏差变化率作为模糊控制器输入量，通过RBF神经网络在线整定模糊控制的权重因子和比例因子，实现导引指令的自适应调整。仿真结果表明，同常规方法相比，在充分考虑随机扰动和测量误差情况下，具有更强的自适应性与鲁棒性，保持了较高的导引精度。

修正弹；滤波外推； RBF神经网络；模糊控制；落点预测

随着火箭推进技术的发展，远程弹道修正火箭弹已经表现出在射程上的强大竞争优势。同时，弹道特征也更加复杂化，飞行时间长、飞行速度涵盖范围更广、飞行高度涵盖了稠密大气层到稀薄大气层的更大空域，弹道过程中受到的随机扰动更加明显，系统误差的积累更大。这就要求火箭弹制导控制方法在确保导引精度的同时，对随机扰动和系统误差的调整具有更高的鲁棒性和自适应性。

滤波外推落点预测导引法，是目前弹道修正火箭弹广泛应用的一种制导方法。其工作原理为：弹载传感器实时测量弹体运动参数，后经滤波处理代入线性化弹道方程外推得到落点位置偏差及偏差变化率，进而再通过线性导引方程形成舵机控制指令[1]。弹道末端修正效果与落点预测精度有关，还与导引方程密切相关。在提高预测精度方面，国内外学者进行了大量研究：李兴隆等提出了线性弹道模型预测法，提高了六自由度弹道落点预测精度和解算速度[2]；李超旺等将摄动理论应用到火箭弹落点预测中，分析了扰动情况下的弹道解算方法[3]；Leonard 等提出了通过修正线性理论进行快速弹道预测的方法，减小了弹道方程线性化造成的预测误差[4]。目前，在导引方程设计方面，将先进控制理论与落点预测导引法相结合的相关研究还不深入。

1 问题的提出

火箭弹末端修正为高动态过程，且实际存在各种随机扰动和测量误差。此外，为了有效地打击低速机动目标，要求弹道落点满足设定落角等多种角度约束，因此，要求设计的制导算法具备良好精度的同时，还应兼具一定的自适应性和鲁棒性。而目前，滤波外推落点预测导引中，通常导引方程为关于落点位置偏差及偏差变化率的线性方程：

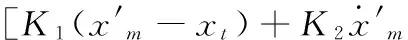
(1)

为了减小导引精度对卫星测量精度的依赖程度，文献[2]提出了利用一定时间内的落点偏差量的加权平均值代替某时刻瞬态值，以提高导引算法的鲁棒性，并给出了加权算法：

(2)

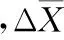
除此之外，通常上述方法中导引系数需要经过一系列的仿真计算、试验和采用经验公式计算确定，通过记录样本数据进行插值拟合得到近似的导引系数与扰动关系，作为弹体飞行导引系数在线调整的依据。但是，这种方法得到的样本数据涵盖范围小，且一经确定不能改变，导引效果不理想，过程复杂且不通用，自适应性与鲁棒性较差。

模糊控制是一种非线性智能控制方法，因无需对被控对象建立数学模型、构造容易、实现简单而得到广泛应用。带自调整因子的模糊控制器，通过优化算法在线调整输入量的权重因子改变控制规则，增强控制器的自学能力和自适应性，从根本上提高模糊控制性能。动态RBF神经网络具有对非线性系统动态寻优逼近的能力，可作为带自调整因子模糊控制器控制参数在线调整的依据。二者结合可以对常规滤波外推落点预测导引法的导引方程进行优化，增强自适应性和鲁棒性，同时保持导引精度。因此，本文提出了一种基于模糊控制理论和动态RBF神经网络在线辨识理论的落点预测导引法。

2 设计原理与方法

2.1 导引控制器总体设计

图1 基于RBF网络辨识和模糊控制的预测导引原理图

2.2 自调整模糊控制器设计

带自调整模糊控制原理如图2所示，具体控制器解析表达式为[5]：

膨润土矿床类型分为火山岩型、火山-沉积型、沉积型、侵入岩型四种，以沉积(含火山沉积)型为最多，储量占全部储量的70%以上。膨润土矿的颜色有白色、乳酪色、淡灰色、淡黄绿色、淡红色、褐红色以及黑色、斑杂色等，具有油脂光泽、蜡状光泽或土状光泽，断口常为贝壳状或锯齿状。采出原矿有块状、微层纹状、角砾状、土状及斑杂状等，微细结构以泥质结构为主，也有变余火山碎屑、角砾凝灰及粉砂状结构等。

U=-〈αE+(1-α)EC〉·Ku(0≤α≤1)

(3)

其中，α为权重因子，e为系统误差，E、Ec为模糊化后的系统误差和误差变化率，Ku为输出控制量的比例因子，通过调整α和Ku可以改变模糊控制器输出。根据模糊控制原理，取E、Ec、U论域均为{-6 6}[5]，E的模糊子集{NB,NM,NS,NO,PO,PS,PM,PB},Ec和U的子集为{NB,NM,NS,ZO,PS,PM,PB}。隶属度函数曲线分别如图3、图4所示，形成的模糊规则如表1所示。

图2 带自调整因子的模糊控制原理图

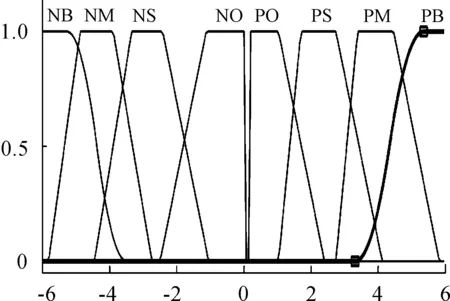
图3 输入量E的隶属函数曲线

图4 输入EC和输出U的隶属函数曲线

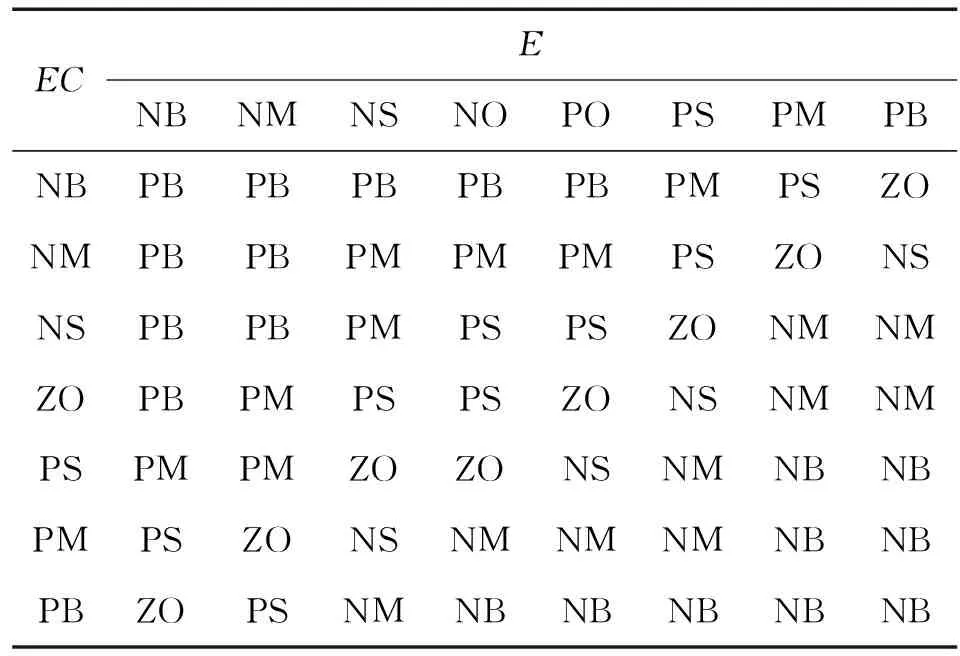
ECENBNMNSNOPOPSPMPBNBPBPBPBPBPBPMPSZONMPBPBPMPMPMPSZONSNSPBPBPMPSPSZONMNMZOPBPMPSPSZONSNMNMPSPMPMZOZONSNMNBNBPMPSZONSNMNMNMNBNBPBZOPSNMNBNBNBNBNB

具体参数在线调整准则：当误差较大时，控制器主要任务是减少误差，提高响应速度，应该增大误差权重和比例因子系数。相反，误差减小时，控制器主要任务是尽快进入稳态，减小超调，应该增大误差变化率的权重，减小比例因子系数。因此，参数调整的一种线性表达式为：

(4)

Ku(k)=Ku(k-1)+kupE(k-1)+

(5)

其中，N为输入误差的量化等级，kup、kui、kud为比例因子计算的比例、积分、微分系数。

由式(3)～(5)能够实现控制量在一定程度上的自适应调整，但是由于参数在线调整算法相对简单，模糊控制器适应范围小、对误差变化敏感度低、控制性能不高。因此，引入RBF神经网络辨识算法提高参数在线调整能力。

2.3 动态RBF神经网络辨识器设计

常规的RBF神经网络虽然能够以任意精度逼近任意非线性函数，具有强大的非线性映射能力，但须事先确定隐层节点个数，网络结构固定，适应性差。 基于最近邻聚类学习算法的RBF神经网络，无须事先确定隐层节点个数，网络结构动态改变，完成聚类所得隐层节点个数最少，结构最优[7,8]。

基于RBF神经网络的模糊控制器工作原理如图5所示。其中参数α0、αs、α、ku整定公式推导具体如下：

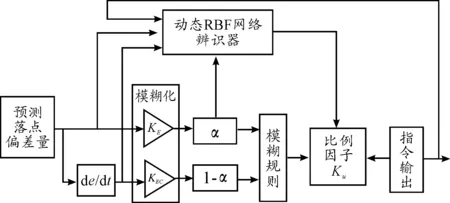
图5 基于RBF和模糊控制的制导原理图

动态RBF网络输入向量为：

(6)

式中δc为模糊控制器输出的舵偏指令，动态RBF网络辨识的输出向量为：

Y=[α0αsku]T

(7)

离散化系统输入输出为：

Xk=[Δx(k-1),Δx(k-2)…Δx(k-m1),

δc(k-1),δc(k-2)…δc(k-n1)]T

(8)

(9)

式中，n1、m1为输入量延时步数，n为k时刻动态RBF神经网络隐单元个数。

动态RBF神经网络辨识器对模糊控制参数进行在线辨识，获得Jacobian信息计算控制参数并送往模糊控制器，以调节模糊输入权重系数，Jacobian矩阵为：

(10)

式中ωi,Ci均为输入量每次在线更新的权值；RBF网络的性能指标为：

(11)

采用增量公式计算模糊控制参数：

Y(k)=Y(k-1)+Δy

(12)

(13)

已知α0、αs∈[0,1]，则需要对输出α0(k),αs(k)进行归一化：

(14)

然后利用式(2)计算α(k)，并向模糊控制器输出参数向量[α,ku]。

3 仿真算例

为了对比本文方法与传统滤波外推导引法在随机扰动和系统误差存在的情况下的导引效果，以某型远程火箭弹弹道末段为导引控制条件，以GPS/地磁陀螺为导航方式，以单通道控制的“十”字气动鸭舵提供所需修正力，取基于卡尔曼滤波的落点预测导引法为仿真对比导引法。两种导引法均选择在弹目纵向距离为6～0.1 km阶段，且只考虑纵向平面导引控制。起控点弹道初始条件见表2。为了突出体现导引算法的特性，分析了弹道末段对制导控制系统影响较大的几类随机扰动和误差值，极限大小如表3所示。

表2 起控点弹道初始条件

表3中列出的初始扰动可以通过修改仿真初始弹道条件实现；阵风扰动在仿真开始后施加在弹道模型中；控制误差和测量误差服从正态分布，存在于整个末制导过程，通过生成随机数的形式叠加到仿真模型中。

表3 随机扰动和误差量极限值

仿真条件一：在误差范围内，改变阵风风速进行仿真，以验证RBF网络辨识输出权重因子α和比例因子Ku的自适应性；仿真条件二：所有干扰和误差均取极大值，相同条件下与传统滤波外推落点预测导引律进行仿真对比，以验证极限条件下新导引法的导引效果。

由图7、图8可知，当扰动施加时，预测落点偏差增大，RBF神经网络辨识器输出的模糊控制权重因子α和比例因子Ku均取较大值；随着控制时间的积累，二者逐渐减小并趋于稳定。不同风速的阵风干扰下,RBF网络辨识器均可通过改变输出系数大小，有效地实现输出的自适应调整。

由图9可知，在扰动和误差存在下，滤波外推导引法弹道曲率变化较大，落点距目标点纵向偏差为56.23 m；新导引法弹道平直，落点纵向偏差12.13 m。可见，在随机扰动和测量误差极限情况下仍可获得更好的弹道轨迹，较高的导引精度。

图7 权重因子α自调整曲线

由图10、图11可知，存在测量误差和控制误差的前提下，扰动施加后滤波外推法计算的舵偏角发生突变，致使弹体所受过载发生长时间振荡；新导引法舵机控制指令并未发生突变，弹体所受过载很快趋于稳定，变化平稳。而且，扰动施加时新导引法响应更快，通过增大输出舵偏角迅速减小干扰造成的偏差，使系统尽快趋于稳定；进入稳定后，通过逐渐减小指令舵片角，以进一步减小落点预测偏差。可见，基于RBF神经网络辨识和模糊控制的导引法提高了导引系统的鲁棒性。

图8 比例因子Ku的自调整曲线

图10 指令舵偏角对比

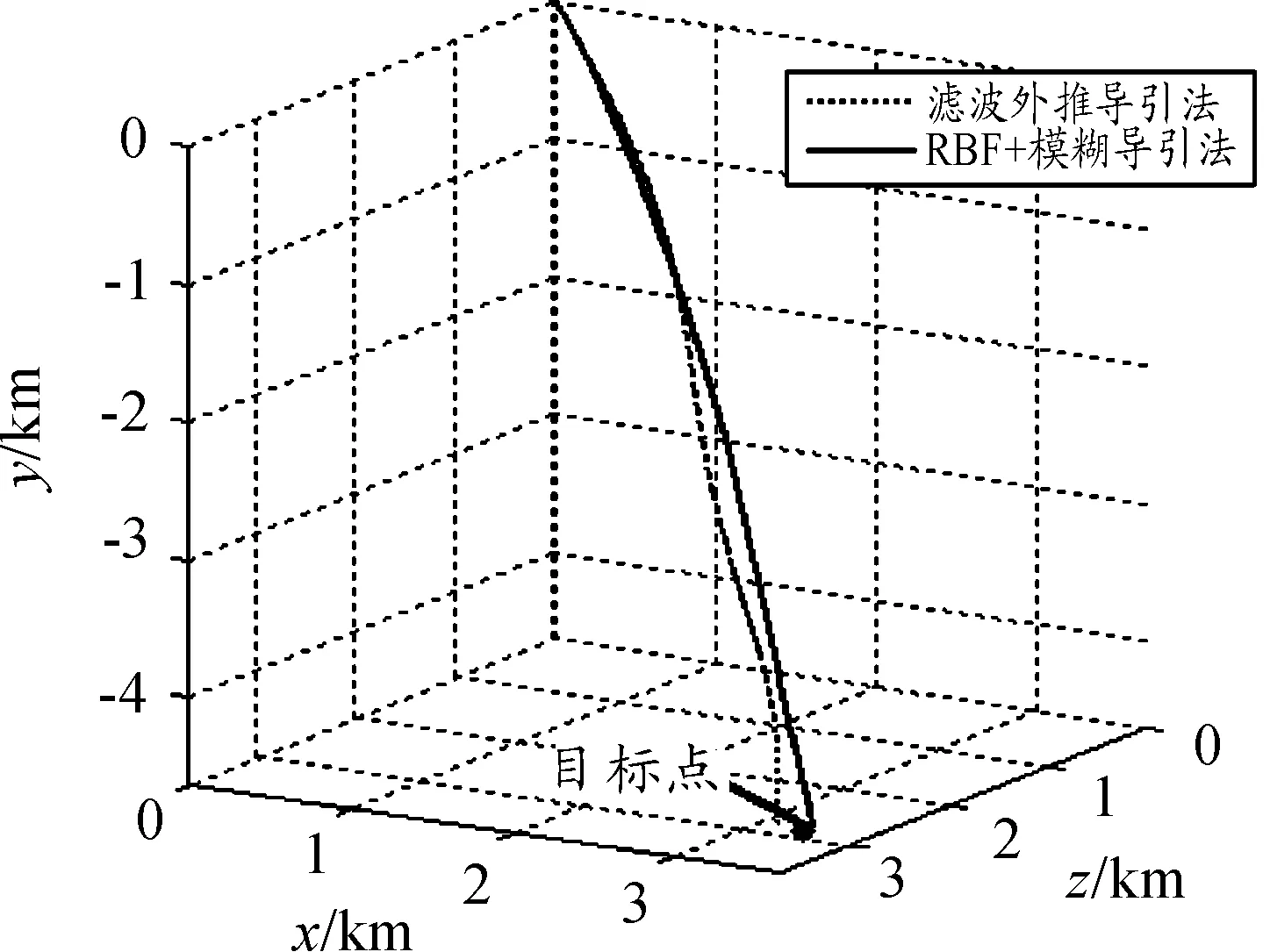
图11 弹体过载对比

4 结论

为了提高传统滤波外推落点预测导引法自适应性和鲁棒性，提出了一种基于模糊控制理论和动态RBF神经网络在线辨识理论的落点预测导引律。将滤波外推预测得到的落点偏差与偏差变化率作为带自调整因子模糊控制器输入量，通过动态RBF神经网络在线整定模糊控制的权重因子和比例因子，实现制导指令的自适应调整。仿真表明，在随机扰动和测量误差极限情况下仍可获得较高的导引精度，导引指令自适应性、鲁棒性更强。

[1] 杨俊，钱宇.基于预测落点导引律的制导炸弹中制导律设计[J].计算机仿真，2011,28(8):87-91.

[2] 薄学纲，韩晶，焦国太等.基于落点预测的火箭弹变系数末制导律[J].探测与控制学报，2015,37(5):84-88.

[3] 李超旺，高敏，宋卫东等.基于摄动原理的火箭弹实时预预测[J].兵工学报，2014,35(8):1164-1171.

[4] HAINZ L C，COSTELLO M．Modified projectile linear theory for rapid trajectory prediction[J].Journal of Guidance，Control，and Dynamics,2005,28(5):1006-1014.

[5] 王晓侃，王蕾，孙忠良等.基于自调整因子模糊控制器的设计与研究[J].机电一体化，2009(12):35-37.

[6] WANG Xiao-kan,SUN Zhong-liang,Design and Research Based on Fuzzy PID-parameters Self-tuning Controller with MATLAB;2008 International Conference on Advanced Computer Theory and Engineering (ECACTE 2008)[C].Phuket Thailand:IEEE CPS,2008:996-999.

[7] 李绍铭，刘寅虎.基于改进型RBF神经网络辨识的PID控制[J].自动化与仪表，2006(6):40-43.

[8] 刘铁男，段玉波，刘志德等.带优选聚类算法的RBF网络辨识器及应用[J].控制与决策，2003,18(2):233-236

(责任编辑 杨继森)

Research on Trajectory Prediction Guidance Law Based on Dynamic RBF Network Identification and Fuzzy Control

FENG Yao-xuan1, BO Xue-gang2

(1.College of Mechatronic Engineering，North University of China，Taiyuan 030051，China;2.Jiangsu Yongfeng Mechanical Liability Co., LTD., Nanjing 210014, China)

Aiming at the problem that guidance coefficient is difficult to determine, and guidance precision is low, and poor adaptability and robustness, a target prediction guidance law based on dynamic RBF neural network on-line identification and fuzzy control theory with self adjustment factor was presented. Specifically, on the basis of the extrapolation filter upload target prediction guidance method, we took the impact point deviation and deviation change rate as the fuzzy controller input. Through the RBF neural network, the weights of the fuzzy control and the proportion of the whole set of fuzzy control, we achieved the adaptive adjustment of the guidance commands. The simulation shows that high accuracy of the measurement error can be obtained, and the guidance instruction is more adaptive and robust compared with the conventional method, considering the random disturbance and the measurement error,.

correction projectile; filter extrapolation algorithm; RBF neural network; fuzzy control; target prediction

2016-10-19；

2016-11-15

冯耀暄(1995—)，男，硕士研究生，主要从事制导与控制技术研究。

10.11809/scbgxb2017.02.025

冯耀暄，薄学纲.基于动态RBF网络辨识和模糊控制的弹道落点预测导引研究[J].兵器装备工程学报，2017(2):108-112.

format:FENG Yao-xuan, BO Xue-gang.Research on Trajectory Prediction Guidance Law Based on Dynamic RBF Network Identification and Fuzzy Control[J].Journal of Ordnance Equipment Engineering,2017(2):108-112.

TP273

A

2096-2304(2017)02-0108-05