太阳影子定位的时空分析
2017-03-15张志鹏崔克楠李厚彪
张志鹏,崔克楠 ,李厚彪
(电子科技大学 a.光电信息学院; b.数学科学学院;四川 成都 611731)
太阳影子定位的时空分析
张志鹏a,崔克楠a,李厚彪b
(电子科技大学 a.光电信息学院; b.数学科学学院;四川 成都 611731)
该文研究了利用太阳影子进行定位的正演和反演问题。基于太阳下直杆影子长度的变化,利用球面三角函数,建立了影长与日期、时间、经度、纬度、太阳高度角的关系模型,并对此模型进行反演,得到了已知影长变化求解时空定量的方法;并采用定值匹配搜索与最小二乘拟合两种不同算法进行了对比检验,并对此数学模型进行了基于大气折射的误差分析及修正。
最小二乘拟合;匹配搜索;太阳影子定位;太阳高度角
太阳影子定位是一种基于球面三角函数[1]分析得到阳光下物体影子长度变化规律与其影响因素,即经纬度、日期、太阳高度角[2]的关系,并利用这些关系进行反演获得测试点的时空位置的一种方法。在军事行动、文物探测、森林探险等领域,太阳影子定位具有现实意义。
在利用搜索算法时,其搜索精度是要着重考虑的一项内容,本文针对搜索结果做出相应的灵敏度和误差分析。相对于常用的GPS和北斗定位来说,由于其测量都是在地面上进行,所以不可避免地受到天气、大气折射的影响。卫星定位是在太空中进行,其载体是电磁波而不是自然光,相对来说其受大气折射的影响可以忽略不计。对于利用自然光为载体的太阳定位,本文将结合光学知识提出关于大气折射的修正意见。
1 影长关系表达式求解
首先,在不考虑太阳折射的情况下,太阳直射时的影子成像原理如图1所示。
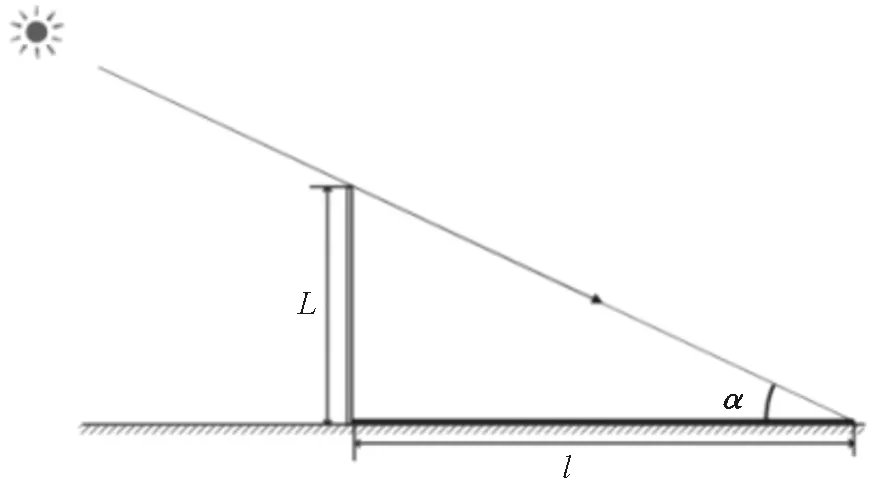
图1 太阳照射物体影子示意图
利用三角函数公式,从图1可以直接推出:
(1)
式中,α为太阳高度角,L为直竿长度,l为阴影长度。
另外,根据如图2所示的太阳高度角相关因素球面函数图,利用球面三角函数公式,可以推导出太阳高度角与经纬度、时角的关系表达式为:
sinα=sinψsinδ+cosωcosψcosδ
(2)
式中,ψ为纬度,δ为太阳赤纬角,ω为时角。
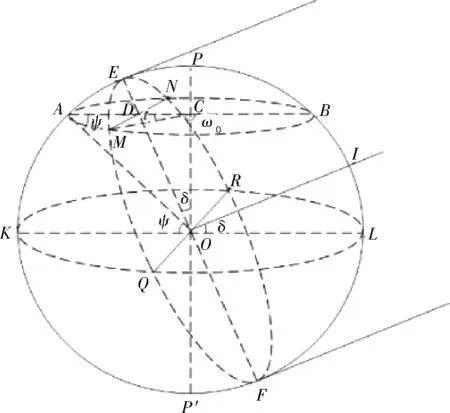
图2 太阳高度角相关因素球面图(注:图中ω0为日出时角)
查阅资料知太阳赤纬角[3](单位:度),即太阳直射点纬度与日角的关系如下[4]:
δ=0.372 3+23.256 7sinθ+0.114 9sin2θ-
0.171 2sin3θ-0.758cosθ+
0.365 6cos2θ+0.020 1cos3θ
(3)
式中,θ为日角(单位:度),表示为:
(4)
式中,T为日期修正,由3部分构成:
T=N+ΔN+N0
(5)
式中:N为积日,其值等于测试影长的日期到1月1日的时间,平年最后一天积日为365,闰年最后一天积日为366;ΔN表示积日修正日。
N0=79.676 4+0.242 2(xNF-1985)-
floor((xNF-1985)/4),
(6)
(7)
式中:xNF为年份,在本文中取2015年,此时N0=79.942 4;floor为Matlab中命令,表示向下取整;Ld为经度差修正值;W为时间差修正值,计算公式为:
(8)
(9)
式中,Tc为观测时刻(单位:h),λ为测试点经度。
文献[3]中同时可以查到时角(单位:rad)的表达式为:
(10)
(11)
Eq=0.002 8-1.985 7sinθ+9.905 9sin2θ-
7.092 4cosθ-0.682 2cos2θ
(12)
式中,Trs为真太阳时,Eq为平太阳时和真太阳时时差。
2 公式项的误差分析
2.1 天安门广场的影长变化
在已知北京天安门广场经纬度和日期的情况下,利用前文公式可以计算出对应的影长变化数据。北京天安门广场经纬度为:(116°23′29″E,39°54′26″N),计算出在2015年10月22日北京时间9:00-15:00的影长变化数据并绘制如图3所示(测试杆长为3m)。

图3 天安门广场影长变化
从图可看出,在北京时间12∶15左右影长最短,即太阳高度角最小,北京达到正午时刻。北京的正午时刻不在12∶00的原因是北京时间是东八区中央经线即120°E,而北京的经度为116°23′,时差约为14min左右。
2.2 与专业软件对比的误差分析
利用专业计算太阳高度角的软件“云算笔记”将对应时刻的天安门影长计算出来,与前文公式计算结果对比如图4所示。

图4 阴影长度对比
本文定义平均差异比率为每个时间点差异的比率均值,即:
(13)
式中,η为模型计算得到的影长, 为专业软件计算得到的影长,N为影长总个数。计算结果为:

η值相对较小,表明模型较为可信。
3 已知影长变化反演特定时空
在实际的应用中,通常是在测出一段时间内影子长度变化之后,利用这些数据求出测试点所在的经纬度,在某些特殊情况下,也会需要求出测试的日期。下文将会分成已知日期和未知日期两种情况反演时空。
某地在2015年4月18日测量的一段时间内影长变化数据如表1所示[5]。
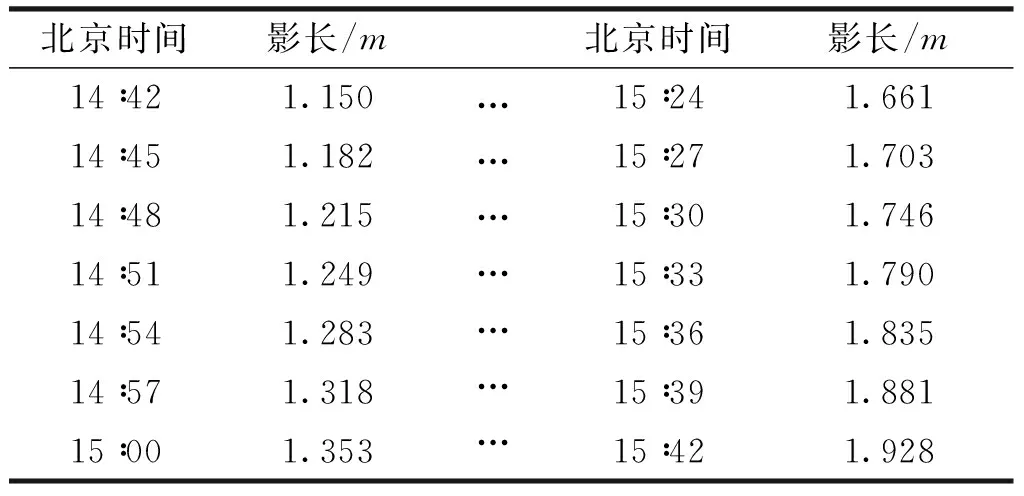
表1 某地直杆影长变化
3.1 已知日期反演空间位置
3.1.1 定值匹配搜索方法
1)确定定值及匹配度
定值匹配可以作为遍历法的一个评判标准,其意为对于每一个搜索点建立统一的标准来判断该点是否符合要求。以二维空间为例,设在遍历法中需要搜寻的点为(xi,yj),在遍历的过程中可以对每个点(xi,yj)求出其匹配程度,从中寻找出匹配度最大的点即为目标点。
对于本模型来说,测试的直杆长度为定值,所以可以将杆长作为匹配对象,对于每个经纬度计算出来不同时间的影长和太阳高度角,进而计算出对应的杆长,时间列下杆长波动最小的就是最优解。
将时间列下杆长的波动程度定义为匹配度,对于上文公式组是一个非线性方程组,带入不同的经纬度不会出现极端值误差,所以可以用方差衡量时间列数据的波动程度,即匹配度用方差衡量表示如下:
(14)
式中,ξ为搜索匹配度,li为计算得到的某个经纬度时刻i的阴影长度,μ为计算得到的某个经纬度所有测量时刻阴影长度的均值。
2)定值匹配方法计算结果
利用式(1)~式(12),对经纬度进行搜索计算出的匹配度如图5表示。

图5 定值匹配搜索匹配度
可以看出,在(109°E,19°N) 附近匹配程度最高。考虑到测量的误差及精准度问题,取1°的误差限进行细精度搜索,即初步定位到:
(109°±1°E,19°±1°N)
3)增大精度小范围搜索
前文已叙述了精度对于定位的重要性,之所以不直接使用细精度进行搜寻的原因是大范围细精度搜索会导致程序时间复杂度无比庞大。太阳影子定位的前景是将其做到智能化和软件化(APP)以使在特殊情况下,如登山、野外生存等情况下能够快速反应,所以直接细精度搜索实际意义不大。
在已经得到整数位级的定位位置后,根据已经设定的1°的误差限,在此范围内进行细精度搜索。
如果此时将误差限设为0.1°,则空间复杂度为400;如果将误差限设为0.01°,则空间复杂度为40 000。相对于现代最普通的计算机来说,这种级别的空间复杂度也可以忽略不计。
4)细精度定位结果及误差分析
根据上述的细精度搜索方法,计算出定位结果为(109.6°E,18.7°N),利用谷歌地图定位在海南省三亚市附近。
实验测试地点经纬度为(109.5°E,18.3°N),其经度误差为:
(16)
纬度误差为:
(17)
其误差相对来说比较小,认为模型较为可信。
3.1.2 最小二乘拟合方法[6]
式(1)~式(12)实际上是一个非线性方程组,也就是说这实际上是一个非线性优化问题。对于已知部分数据的非线性方程组来说,通常有两种解法:1)将已知的数据点带入,组成一个n维的超定方程组(n为已知数据点个数),对于无约束的方程组来说可以用牛顿法解其他参量的最优解,但是对于有约束的超定方程组来说该方法不再适用;2)利用最小二乘法根据已知的数据点对其他参量进行拟合,该方法对有无约束条件不作要求。对于已知影长反演空间位置的问题来说,非线性方程组收到经纬度范围和杆长的约束,用最小二乘拟合更为合适。
1)最小二乘拟合使用
非线性拟合是已知输入向量x和输出向量y,在已经确定拟合函数的情况下, 得到系数向量最优解的方法。而在进行曲线拟合时,常采用最小二乘法进行拟合优化。其求解原理如下:
(18)
当输入一组实验观测数据并设置好初始点后,经过数次迭代,就可以得到确定拟合函数局部最优的参数向量值。
对于本文讨论问题,最小二乘拟合的对象是由式(1)~式(12)组成的非线性方程组,由于日期确定时太阳赤纬角和积日及其修正值可以求出,所以模型对象是杆长与经纬度、影长的关系式:
l=f(L,ψ,λ)
(19)
2)最小二乘方法结果

表2 最小二乘法结果(已知日期)
3.2 未知日期反演空间位置和时间
对于未知日期的情况,相对于已知日期的情况下多了一个时间决策变量,由式(5)~式(9)可知,时间决策变量可以视为积日N,所以此时影长的关系式变为:
l=f(L,ψ,λ,N)
(20)
如果此时采用搜索方法,其算法空间复杂度最小为2.365 2×107,在如此大的空间复杂度下经纬度尚只能精确到1° ,所以此时采用搜索方式不合适。采用最小二乘法拟合时相对于已知日期时只需多增加一个拟合对象N。
拟合结果为如表所示。

表3 最小二乘法结果(未知日期)
4 定值搜索和最小二乘拟合算法步骤

图6 算法流程图
5 大气折射产生误差的修正意见
地球表面向太空方向大气层被分为了对流层、平流层、中间层、暖层和稀薄的散逸层[7],不同层的大气折射率不同,这也就导致了太阳光的折射,前文建立的模型并没有考虑折射带来的影响。太阳光的折射示意图如图7所示(稀薄的散逸层忽略)。
由斯涅尔定理(折射定理)可得[8]:
n0sinα=n1sinα1=n2sinα2=
n3sinα3=n4sinα4
(20)

图7 大气折射太阳光路图
所以实际太阳高度角为:
(21)
其中,n0~n4分别是太空、暖层、中间层、平流层和对流层的折射率。
6 结束语
本中利用计算机算法实现利用太阳影子进行定位,整体过程中尽量避免了主观性因素,使得定位结果相对准确。定位过程采用了匹配思想和拟合思想,两种方式适合不同需要情况,决策变量较少时选用搜索算法较为准确,决策变量较多时选用最小二乘拟合方法更契合实际。同时本文提出了定位过程中大气折射影响的修正意见,在已知实时对流层和暖层折射率时可使结果更准确。
目前,国内和国际对太阳影子的精确定位还没有很多研究,此类研究对于卫星信号相对较差的极端天气或恶劣地带的定位有实际意义。
[1]王昌明.可照时数和太阳高度角计算公式的简化证明[J].山东气象, 1989(2): 46-48.
[2]王国安, 米鸿涛, 邓天宏,等.太阳高度角和日出日落时刻太阳方位角一年变化范围的计算[J].气象与环境科学, 2007(9):161-164.
[3]张闯, 吕东辉, 顼超静.太阳实时位置计算及在图像光照方向中的应用[J].电子测量技术,2010(11):87-89.
[4]全国大学生数学建模组委会.2015高教社杯全国大学生数学建模竞赛A题—太阳影子定位[EB/OL].(2015-09-12)[2016-10-20].http://www.mcm.edu.cn/html_cn/block/8579f5fce999cdc896f78bca5d4f8237.html.
[5]龙辉平, 习胜丰, 侯新华.实验数据的最小二乘拟合算法与分析[J].计算技术与自动化,2008(27):20-23.
[6]李延兴, 胡新康, 赵承坤,等.光电信号在大气层传播中由于折射产生的路径弯曲[J].中国科学:D辑, 1998(22):149-152.
[7]陈琳.斯涅尔定律数字模型的设计[J].教育技术导刊, 2009(2):9-10.
[8]葛耀林.便携式实时太阳夹角计算装置的实现[J].工业设计, 2011(3):96-97.
[9]谈小生, 葛成辉.太阳角的计算方法及其在遥感中的应用[J].国土资源遥感, 1995 (2): 48-57.
[10]李小文,高峰,王锦地.单一太阳角BRDF数据反演过程中误差传播的估计[J].中国科学:E辑, 2000(30): 6-11.
Temporal and Spatial Analysis of the Sun Shadow Positioning
ZHANG Zhipenga, CUI Kenana, LI Houbiaob
(a.School of Optoelectronic Information; b.School of Mathematics Sciences, University of Electronic Science and Technology of China, Chengdu 611731, China)
The problem of forward and inversion of location methods with sun shadow are studied in this paper.Based on the change of shadow length, by using spherical triangle function, a relational model between shadow length with data, time, longitude, latitude and solar zenith angle is established.And then using this expression to carry out inversion, specific time and testing place can be got by the shadow length change.In the time and space location, two different methods are compared by using the matching search and the least square, respectively.Finally, the error analysis and correction based on the atmospheric refraction are isproposed.
least squares fitting; matching search; sun shadow positioning; solar elevation
2015-10-23;修改日期:2016-10-11
四川省科技支撑计划项目(M110474012015GZ0002);电子科技大学教改项目(2015XBJX0041,2016XJYYB037);高等学校大学数学教学研究与发展中心项目(CMC20160403)。
张志鹏(1995-),本科,主要从事数学建模和微电子器件以及FPGA电路设计的研究。
李厚彪,副教授,lihoubiao 0189@163.com。
O151.2
A
10.3969/j.issn.1672-4550.2017.01.011
