简化的混合域全波形反演方法及GPU加速

桂 生,刘 洪,李 飞

(1.中国科学院地质与地球物理研究所,北京100029;2.中国科学院油气资源研究重点实验室,北京100029)

简化的混合域全波形反演方法及GPU加速

桂 生1,2,刘 洪1,2,李 飞1,2

(1.中国科学院地质与地球物理研究所,北京100029;2.中国科学院油气资源研究重点实验室,北京100029)

全波形反演(FWI)方法综合利用叠前地震波场的动力学和运动学信息,能够高精度地重建地下介质模型参数场,但巨大的计算量一直是制约其发展的一个重要因素。GPU组成的高性能计算集群为提高全波形反演计算效率提供了重要的硬件基础。基于GPU平台,采用简化的混合域全波形反演算法实现了更快速的三维全波形反演计算。首先简单介绍了GPU加速技术应用于简化的混合域全波形反演时的一些优化技巧,包括线程调度、GPU之间数据传输以及共享内存的使用等,然后通过多GPU全波形反演测试了简化的混合域全波形反演的效果,证明了GPU加速技术能够有效地提高全波形反演的计算效率,相比CPU具有十几倍的加速比。

GPU技术;高性能计算;GPU技术优化;全波形反演

全波形反演最初由LAILLY[1]和TARANTOLA[2]等人提出,他们以波动方程为基础,建立模拟数据和观测数据差值的目标函数,通过使其最小化来获得模型的更新量,其模型更新量由梯度和搜索步长决定,梯度可由入射波场和残差反传的波场计算得到。目前已经发展出了多种全波形反演(FWI)方法,按照不同求解波动方程的计算域,大致可分为时间域反演[3-8]、频率域反演[9-11]和Laplace域反演[12-13]。按照求解方式不同又可分为局部梯度类迭代反演[2-3,14-15]和全局优化搜索反演[16-19]等。

无论是时间域、频率域还是Laplace域,巨大的计算量是FWI瓶颈之一。近年来高性能计算技术的发展使这一问题得以缓解。高性能计算的主要发展思路是并行计算。相对于CPU而言,GPU的多线程、多处理器的并行结构更能够满足高性能计算的发展需要[20],而且在相同计算能力的情况下,GPU具有功耗小、价格低等特点。在GPU中,用来进行数据处理的晶体管占据大部分空间,只有少量晶体管用来进行指令流控制和数据缓存[21]。利用GPU进行密集型科学计算是一种潜力巨大且性价比高的解决方案[22]。

由于GPU具有对密集型计算任务加速的优势,因此GPU技术被广泛应用于正演模拟、叠前偏移、逆时偏移、多次波压制以及全波形反演等地震数据处理。MICIKEVICIUS[23]用GPU实现了三维有限差分法计算,并提出了单通法和双通法两种优化策略,也是目前常用的程序优化方法。WANG等[24]研究了基于随机边界条件的GPU加速时间域全波形反演算法,LUO等[25]实现了多GPU的两级并行的全波形反演,MAO等[26]利用GPU加速实现了二维多尺度时间域全波形反演。KIM等[27-28]利用GPU加速实现了三维声波混合域全波形反演的快速计算。SHIN等[29]实现了单GPU的三维Laplace域的全波形反演,GOKHBERG等[30]用谱元法在CPU/GPU异构集群实现了全波形反演,张猛[31]对CPU/GPU平台上全波形反演的各种实用问题进行了分析。LIU等[32]实现了三维混合域全波形反演,但其宽度较窄。YANG等[33]在GPU平台上实现了二维时间域的全波形反演。由于GPU的显存限制,以往的研究多是针对二维或者小规模的三维全波形反演,为克服这一限制,本文采用多GPU动态加载并行方案,针对不同大小的数据采用不同的并行方案,当计算数据过大时,采用区域分解的方法,从而可以实现大规模三维全波形反演;采用简化的混合域全波形反演,能够更快速的计算从以往的单GPU加速到现在的多GPU加速;最后利用Overthrust模型测试了本文方法的可行性和有效性。

1 GPU架构及程序优化

1.1 GPU架构

GPU体系架构如图1所示。

图1 GPU运算单元结构[21]

首先从硬件架构上对GPU进行并行层次分析。GPU主要由两部分组成,一部分是流处理器阵列,另一部分是存储器系统,两部分连接在同一片板卡上。如图1所示,其中多个线程处理器群(Thread Processing Cluster,TPC)组成了一个流处理器阵列,其中每个TPC中有2～3个流多处理器(Streaming Multiprocessor,SM),每个流多处理器中包含8个流处理器(Streaming Processor,SP)[34]。在GPU中最基本单元是SP,SP是由算术逻辑运算器、加法器、乘法器以及寄存控制器组成。SP可以在一个时钟周期内完成一次逻辑运算,或一次32位浮点数加法或乘法运算等。从硬件架构上看,一个流多处理器相当于一个8路单指令多数据流(Single Instruction Multiple Data)处理器,称之为单指令流多线程(Single Instruction Multiple Thread,SIMT)[21]。

图2为统一计算设备架构(Compute Unified Device Architecture,CUDA)编程模式示意图,可以看出,核函数将线程划分为网格(Grid)形式,每个网格又被分成无数个线程块(Block),一定数量的线程(Thread)组成(一般不超过1024个线程)一个线程块。ThreadIdx和BlockIdx是用来标明线程号和线程块号的CUDA内置变量。在核函数中每个线程都有一个唯一的偏移量,偏移量可以通过线程号、线程块号以及线程维度信息计算得到。在一维情况下偏移量等于线程号即为ThreadIdx.x;在二维情况下且Block大小为(Bx,By)的时,计算线程偏移量公式为ThreadIdx.x+ThreadIdx.y×Bx;而在Block大小为(Bx,By,Bz)的三维情况下,线程偏移量计算公式为ThreadIdx.x+ThreadIdx.y×Bx+ThreadIdz.z×By×Bz。在同一个网格下的不同线程块中线程不能进行通讯,意味着不同线程块中线程无法进行数据传输,它们完全并行且独立执行。

与CPU相比,GPU在计算能力和存储器带宽上有显著优势,面对相同量计算任务,GPU所需要的硬件成本和计算功耗都低于CPU,因此,GPU是大规模高性能计算的明智选择。

CUDA的出现使得基于GPU的通用计算(GeneralPurpose GPU,GPGPU)得到了高速发展。现阶段GPU的浮点运算能力已经达到每秒数十万亿次级别,是X86处理器计算能力的数十倍。但是要发挥GPU巨大的计算优势,就需要对程序进行一定的优化,未经优化的程序反而会降低程序的计算效率。

图2 CUDA编程模式[21]

图3对比了CPU和GPU的微观硬件架构,可以看出CPU和GPU计算能力差异巨大的原因。图中ALU(Arithmetic Logic Unit,算术逻辑单元)是计算单元,CPU只具有很少的ALU,而GPU则具有大量的ALU;CPU具有大量的数据缓存和逻辑控制单元,而GPU的数据缓存和逻辑控制单元较少,这就导致GPU的计算能力要远远高于CPU的计算能力,但数据读取以及逻辑运算能力较差,因此GPU非常适合处理计算密集型和并行度较高的计算问题。在FWI中,波场的正传、反传以及梯度计算的计算量所占比例最大。本文的波场正传和反传均采用时间域有限差分算法,有限差分算法中,每个点都是离散的,其计算是独立的,可以同时进行,因此GPU非常适合这种细粒度并行计算。根据计算阶数的不同需要不同个数的邻近网格点上一个时刻的值,因此在计算时需要采用共享内存方式存储邻近网格点的数值,隐藏访存延迟。GPU高性能计算用于地震波有限差分数值模拟能大大提高计算速度,并且具有更小的能耗。梯度的计算也每个点独立计算,不涉及和其它网格点的数据交换,属于细粒度的并行,因此采用GPU同样能提高梯度的计算效率。如何根据FWI的求解区域分配计算任务、如何传输数据以及如何发挥GPU的最优计算性能都需要根据硬件信息以及算法进行优化,其中包括线程块的大小、多GPU之间的数据传输、共享内存的使用等。

1.2 线程调度

在GPU中最基本的执行单元是线程,其次是线程块,每个线程块的大小影响着计算性能,线程块中的每一个线程被发送到一个SP上。每个SM上有8个SP,每个SM最多可以同时执行8个线程块。SM最多能执行的线程数量和线程能使用的资源相互矛盾,一个SM里同时执行的线程越多,就越能隐藏线程访存延迟,这样每个线程能使用的资源相对就越少,因此需要选取适当的线程块大小,使两者平衡,从而得到最优的执行效率。不同的硬件拥有的计算资源不一样,为充分利用硬件资源需要进行测试分析。

本文采用12阶规则网格有限差分法进行波场正传和反传计算。为此,我们使用NVIDIA Tesla K20m GPU对此算法进行了测试分析。三维模型大小256×256×256,网格间距10m。

图3 CPU的微观架构(a)和GPU的微观架构(b)对比

图4中横坐标表示线程块大小,纵坐标表示某一个时刻的计算时间(ms),从图中可以看出,刚开始随着线程块大小的增加,计算时间逐渐减少,这是因为每个SM上执行的线程数量随着线程块大小的增加而增加;当线程块中的线程数量增加到32×32时,计算时间反而急剧增加,这是因为过大的线程块增加了寄存器的使用数量,使得能同时计算的线程块数量减少,同时执行的线程数量也减少所致。综合考虑线程块大小及其使用资源数量,我们进行12阶交错网格有限差分计算时采用的线程块大小为32×16。

图4 不同线程块计算时间对比

1.3 多GPU优化

当计算的数据体十分巨大时,单个GPU显存无法满足计算需求,需采用多GPU并行方案将数据进行区域分解,每个GPU运算一个区域。这样不仅能克服单个GPU显存较小的问题,同时由于多个GPU并行计算,提高了计算效率,减少了计算耗时。我们以规则网格12阶有限差分进行测试,网格大小256×256×256,网格间距10m。

图5中横坐标代表GPU数量,纵坐标代表计算一个时刻波场的计算耗时,从图中可以看出,随着GPU的增多,计算时间成线性减少,理想情况下应该成倍数减少,但是由于区域分解后需要对分解后的数据进行扩边用来交换数据,保证数据的一致性;同时由于各个GPU之间也需要进行数据交换,增加了计算耗时,因此无法达到理想的情况。

图5 多GPU计算性能对比

利用多GPU进行有限差分计算时,计算边界处需要进行数据交换,数据交换分为两种：一种是数据传输到CPU端,再从CPU端传输到另一块GPU端;第二种是2块GPU在一条PCIE线上时,可以直接利用对等网络(peer-to-peer,P2P)技术进行数据交换(图6),不需要经过CPU,大大减少了传输时间。利用P2P技术传输4GB大小数据,所耗时间为0.11s,不使用P2P技术时的传输时间为0.28s,可以看出P2P技术大大提高了传输速度,特别是针对多GPU全波形反演时频繁的数据交换情况。

1.4 共享内存优化

在使用GPU时,需要将数据传输到GPU上,有两种方法提高传输效率,一是使用锁页内存(其存放的数据传输到GPU不需要CPU干涉)提高传输速度;第二种方法是改进硬件条件,如最新Nvlink技术的传输速度达到80GB/s,是现有PCIE3.0技术传输速度的4倍以上。本文主要是在程序上进行方法的改进,因此采用锁页内存方式提高数据的传输效率。经过测试,使用锁页内存传输4GB大小的数据用时0.13s,而不使用锁页内存传输同样大小的数据,则需要0.17s。

前文谈到,在进行12阶规则网格的有限差分计算时,需要读取网格点邻近点上一时刻的波场,而且需要重复读取。为了避免每次计算都需要单独读取波场值,我们采用共享内存的方式加以解决。计算时,直接在开辟的共享内存区域重复进行高速访存,这样很大程度上提高了有限差分法的计算效率。图7 为共享内存示意图,其中蓝色部分是需要计算的点,黄色部分是边界上需要多余读取的数据点。由图可知共享内存实际存储的数据要比计算数据大,以12阶规则网格为例,实际存储的数据大小为12nx+12ny+ny×nx,其中nx为计算区域x方向的网格点数,ny为y方向的网格点数。测试发现,使用共享内存比未使用共享内存的程序加速比高2.6倍。

图6 P2P技术原理

图7 共享内存示意

2 简化的混合域FWI方法GPU实现

对于三维全波形反演,频率域FWI的正传和反传均需要存储巨大的阻抗矩阵,而时间域FWI梯度计算太复杂[35]。因此,本文基于混合域思想对其进行简化。简化的方法是将波场的正传和反传都放到时间域求取,利用离散傅里叶变换(DFT)抽取相应波场的频率成分,在频率域求取残差,再用离散傅里叶反变换(IDFT)将频率域残差返回时间域进行反传;然后将反传时间域波场再次用DFT转换到频率域波场,在频率域求取梯度场。为了方便GPU实现,简化的频率域方法直接在时间域进行残差计算,然后将残差波场反传并用DFT转换到频率域,在频率域求取梯度。简化的混合域全波形反演流程如图8所示。

图8 简化的混合域全波形反演流程

图8中蓝色部分是利用GPU实现的,需要注意的是对于单个节点来说数据加载是动态的,根据计算数据的大小和现有计算资源动态选取并行方案。在炮循环之前,程序会读取各个节点的硬件信息,主要是GPU的个数和单个GPU的显存大小,当需要计算的数据小于GPU的显存时,采用一个GPU计算一炮地震数据,如图9所示。

当需要计算的数据大于单个GPU的显存时,系统会根据实际需要的显存数量以及GPU个数动态地将数据进行区域分解,以获得最佳的计算性能,这时每个GPU将计算一小块反演区域的数据,如图10a 所示(本文指定z方向划分)。

同时由于整个反演区域分解成数个小的反演区域,那么区域边界处就需要进行数据交换,以保证数据的一致性,这样在小数据的边界处增加了交换区域,见图10b。

图9 单GPU未进行区域分解

图10 多GPU区域分解(a)和交换区域增加(b)

GPU实现程序伪代码如下：

读取各个节点的硬件信息;

if(小于单个GPU内存)

{for(炮循环)

根据节点数以及GPU个数信息MPI向各节点发送多少炮数据;

for(单GPU需要计算的炮数循环)

为每个GPU动态发送炮数据

for(时间循环)

每个GPU同时计算一炮数据

}

else(大于单个GPU内存)

{for(炮循环){

根据节点数以及GPU个数信息MPI向各节点发送多少炮数据;

并将每个节点上单炮数据进行区域分解,载入对应的GPU

for(时间循环)

每个GPU计算一小块炮数据

}}

3 模型测试

我们利用SEG的Overthrust模型(图11)对本文方法进行了测试,网格大小801×801×187,网格间距均为10m。地表放炮,共100炮,炮间距40m,x方向和y方向各10炮,第一炮位置位于x=3800m,y=380m处。使用主频为35Hz的零相位雷克子波,采集系统是地表全接收。时间采样率2ms,采样点数为2000。共正演地震数据478GB。反演频率从1.5Hz开始,每次增加1.5Hz,2个频率组成一个频率组,最大频率60Hz。由于计算数据太大,这里动态分配为4个GPU进行处理。

根据节点信息,程序首先将初始模型数据分解成4个小数据体,每个数据体大小如图12a所示,每个GPU负责一个小数据体的计算,其反演结果见图12b,可以看出反演结果和真实模型(图11)能相互对应,在反演结果中能清楚地识别断层之间褶皱成因的背斜。图13a和图13b分别为初始模型和反演结果在x=4000m,y=4000m,z=400m处的切片。由图13a

图11 Overthrust真实模型

可以看出,河道信息比较模糊,无法识别;由图13b可看出,反演结果很好恢复出了河道信息,能有效识别出逆断层,虽然局部信息有差别,但大体都恢复得很好。

采用4节点8核CPU与同样数量的GPU进行对比。在相同任务量(一次迭代计算)的情况下,GPU耗时996s,而CPU耗时14458s,同样数量的GPU相对于CPU其程序加速比达到了14.5倍,可见GPU在FWI的快速计算中具有明显优势。

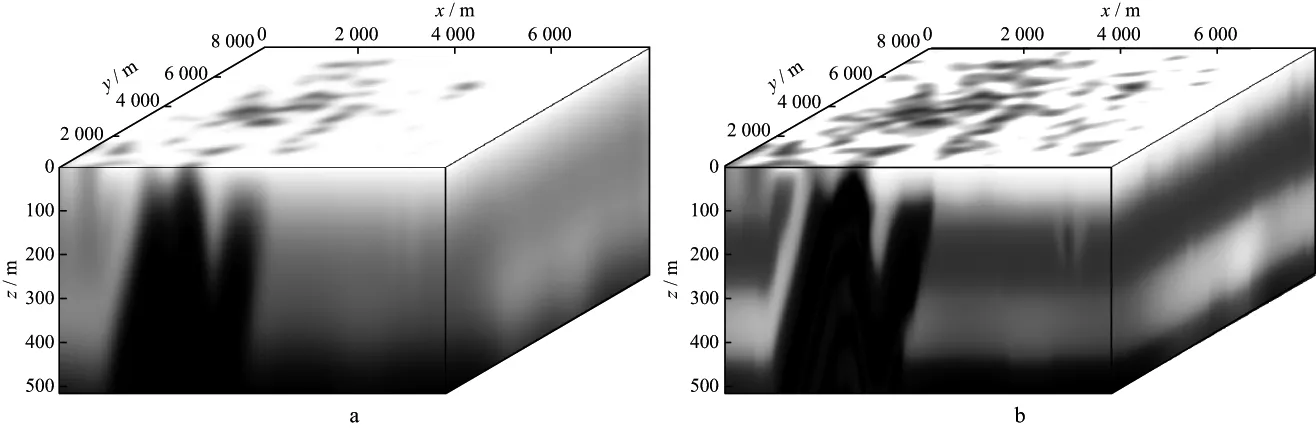
图12 使用4块GPU时,初始模型数据分解成的小数据体(a)及小数据体反演结果(b)(z方向上分解成的4个小数据体之一)

图13 使用4块GPU时,初始模型(a)和反演结果(b)在x,y,z方向上的切片及其连片显示

4 结论

简化混合域方法直接利用时间域数据来实现多尺度反演,与以前的混合域方法相比,流程每次迭代少了一次DFT和IDFT,并且可以获得良好的反演效果。

GPU显存有限,所以针对大规模三维混合域波形反演,特别是叠前大数据的计算,多GPU成为必然选择。在使用多GPU计算时需要对程序进一步优化,才能发挥GPU的最优性能,本文提出的多GPU动态并行方案具有良好的全波形反演结果并具有较好的加速性能,为实现大规模FWI的实际应用提供一种可选择的计算方法和计算框架。

[1] LAILLY P.The seismic inverse problem as a sequence of before stack migrations[C]∥BEDNAR J B.Conference on inverse scattering:theory and application.Philadelphia:SIAM,1983:206-220

[2] TARANTOLA A,NERCESSIAN A,GAUTHIER O.Nonlinear inversion of seismic reflection data[J].Geophysics,1984,49(2):645-649

[3] BLEISTEIN N,COHEN J K,HAGIN F G.Two and one-half dimensional Born inversion with an arbitrary reference[J].Geophysics,1987,52(1):26-36

[4] CRASE E,PICA A,NOBLE M,et al.Robust elastic nonlinear waveform inversion:application to real data[J].Geophysics,1990,55(5):527-538

[5] KOLB P,COLLINO F,LAILLY P.Pre-stack inversion of a 1-D medium[J].Proceedings of the IEEE,1986,74(3):498-508

[6] MARFURT K J.Accuracy of finite difference and finite element modeling of the scalar and elastic wave equation[J].Geophysics,1984,49(5):533-549

[7] PICA A,DIET J P,TARANTOLA A.Nonlinear inversion of seismic reflection data in a laterally invariant medium[J].International Journal of Science Education,1990,55(3):284-292

[8] WANG B L,GAO J H.Fast full waveform inversion of multi-shot seismic data[J].Expanded Abstracts of 80thAnnual Internat SEG Mtg,2010：4453-4459

[9] PRATT G,SHIN C,HICKS.Gauss-Newton and full Newton methods in frequency space seismic waveform inversion[J].Geophysical Journal International,1998,133(2):341-362

[10] SIRGUE L,PRATT R G.Efficient waveform inversion and imaging:a strategy for selecting temporal frequencies[J].Geophysics,2004,69(1):231-248

[11] SONG Z M,WILLIAMSON P R,PRATT R G.Frequency-domain acoustic-wave modeling and inversion of crosshole data:part Ⅱ:inversion method,synthetic experiments and real-data results[J].Geophysics,1995,60(S1):796-809

[12] CHANGSOO S,HO C Y.Waveform inversion in the Laplace domain[J].Geophysical Journal International,2008,173(3):922-931

[13] HA W,SHIN C.Laplace-domain full-waveform inversion of seismic data lacking low-frequency information[J].Geophysics,2012,77(5):R199-R206

[14] GAUTHIER O,VIRIEUX J,TARANTOLA A.Two-dimensional nonlinear inversion of seismic waveforms:numerical results[J].Geophysics,1986,51(7):1387-1403

[15] MORA P.Nonlinear two-dimensional elastic inversion of multioffset seismic data[J].Geophysics,1987,52(9):1211-1228

[16] SEN M K,STOFFA P L.Global optimization methods in geophysical inversion[J].Advances in Exploration Geophysics,1995,4：269-277

[17] SAMBRIDGE M,DRIJKONINGEN G.Genetic algorithms in seismic waveform inversion[J].Geophysical Journal International,1992,109(2):323-342

[18] JIN S,MADARIAGA R.Nonlinear velocity inversion by a two-step Monte Carlo method[J].Geophysics,1994,59(4):577-590

[19] SEN M K,STOFFA P L.Nonlinear one-dimensional seismic waveform inversion using simulated annealing[J].Geophysics,1991,56(10):1624-1638

[20] 赵改善.地球物理高性能计算的新选择:GPU 计算技术[J].勘探地球物理进展,2007,30(5):399-404 ZHAO G S.New alternative to geophysical high performance computing:GPU computing [J].Progress in Exploration Geophysics,2007,30(5):399-404

[21] KIRK D.NVIDIA CUDA software and GPU parallel computing architecture[OB/EL].http:∥kr.nvidia.com/content/cudazone/download/showcase/kr/Tutorial-DKIRK.pdf,2007:103-104

[22] 李博,刘国峰,刘洪.地震叠前时间偏移的一种图形处理器提速实现方法[J].地球物理学报,2009,52(1):245-252 LI B,LIU G F,LIU H.A method of using GPU to accelerate seismic pre-stack time migration[J].Chinese Journal of Geophysics,2009,52(1):245-252

[23] MICIKEVICIUS P.3D finite difference computation on GPUs using CUDA[J].The Workshop on General Purpose Processing on Graphics Processing Units,2009:79-84

[24] WANG B L,GAO J H,ZHANG H L,et al.CUDA-based acceleration of full waveform inversion on GPU[J].Expanded Abstracts of 81stAnnual Internat SEG Mtg,2011:2528-2533

[25] LUO J R,GAO J H,WANG B L.Multi-GPU based two-level acceleration of full waveform inversion[J].Journal of Seismic Exploration,2012,21(4):377-394

[26] MAO J,WU R S,WANG B L.Multiscale full waveform inversion using GPU[J].Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012:7-13

[27] KIM Y,SHIN C,CALANDRA H.3D hybrid waveform inversion with GPU devices[J].Expanded Abstracts of 82ndAnnual Internat SEG Mtg,2012:1-5

[28] KIM Y,SHIN C,CALANDRA H,et al.An algorithm for 3D acoustic time-Laplace-Fourier-domain hybrid full waveform inversion[J].Geophysics,2013,78(4):R151-R166

[29] SHIN J,HA W,JUN H,et al.3D Laplace-domain full waveform inversion using a single GPU card[J].Computers & Geosciences,2014,67(1):1-13

[30] GOKHBERG A,FICHTNER A.Full-waveform inversion on heterogeneous HPC systems [J].Computers & Geosciences,2016,89(3):260-268

[31] 张猛,王华忠,任浩然,等.基于CPU/GPU异构平台的全波形反演及其实用化分析[J].石油物探,2014,53(4):461-467 ZHANG M,WANG H Z,REN H R,et al,Full waveform inversion on the CPU/GPU heterogeneous platform and its application analysis[J].Geophysical Prospecting for Petroleum,2014,53(4):461-467

[32] LIU L,DING R,LIU H,et al.3D hybrid-domain full waveform inversion on GPU[J].Computers & Geosciences,2015,83(1):27-36

[33] YANG P L,GAO J H,WANG B L.A graphics processing unit implementation of time-domain full-waveform inversion[J].Geophysics,2015,80(3):F31-F39

[34] 王泽寰,王鹏.GPU并行计算编程技术介绍[J].科研信息化技术与应用,2013,4(1):81-87 WANG Z H,WANG P.Introduction to GPU parallel programming technology [J].E-Scinence Technology & Application,2013,4(1):81-87

[35] VIRIEUX J,OPERTO S.An overview of full-waveform inversion in exploration geophysics[J].Geophysics,2009,74(6):WCC1-WCC26

(编辑：朱文杰)

Simplified hybrid domain FWI method and GPU acceleration

GUI Sheng1,2,LIU Hong1,2,,LI Fei1,2

(1.InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China;2.KeyLaboratoryofPetroleumResourcesResearch,ChineseAcademyofSciences,Beijing100029,China)

Full waveform inversion comprehensively utilizes the dynamics and kinematics information of the prestack seismic wave field to rebuild accurately the parameter field of underground model.It is the important research orientation in geophysical exploration field of domestic and aboard,but the huge amount of computation has been an important factor which restricts its development.Computing capacity of high performance computing cluster currently consisting of the development of GPU provides an important basis of hardware for the improvement of the full waveform inversion (FWI) to make a more rapid 3D FWI,using the simplified hybrid domain FWI algorithm.We briefly introduce some optimization techniques of GPU acceleration applied to the simplified hybrid domain FWI,including the thread scheduling,GPU and GPU data transfer and the use of shared memory.The test shows that hybrid domain FWI can get a good inversion results.GPU technology can effectively improve the computation efficiency of the FWI and its speedup ratio is ten times more than CPU.

GPU technology,high performance computing (HPC),GPU technology optimization,full waveform inversion (FWI)

2016-09-30;改回日期：2016-12-08。

桂生(1988—),男,博士,主要从事速度建模和计算地球物理研究。

刘洪(1959—),男,研究员,主要从事地震波成像和油储地球物理研究。

国家高技术研究发展计划(863计划)(2012AA061202)资助。

P631

A

1000-1441(2017)01-0099-08

10.3969/j.issn.1000-1441.2017.01.012

This research is financially supported by the National High-tech R & D Program (863 Program) (Grant No.2012AA061202).