Wave equation tomography in baseband with phase correction from the first arrival traveltimes

YIN Feng,Jerry HARRIS

(Department of Geophysics,Stanford University,Stanford 94305,USA)

Wave equation tomography in baseband with phase correction from the first arrival traveltimes

YIN Feng,Jerry HARRIS

(Department of Geophysics,Stanford University,Stanford 94305,USA)

We use the first arrival traveltime to correct the phase distortion in a nonlinear wave equation inversion scheme.This improves the precision of tomographic reconstruction of a velocity structure with large variations and helps solve the ill-posed problem of wave equation inversion.When the variation of the velocity distribution is large,general non-linear wave equation inversions are very ill-posed and for such strong nonlinear we can not obtain a correct inversion.One of main reasons is that the calculated and observed phase of the wavefield differs greatly if the initial model is far from the true model.This leads to highly mismatched phase between the calculated and the observed wave field.This is so-called “Cycle Skipping” problem in the full waveform inversion.The phase mismatch is even more pronounced if a high operating frequency is employed in order to increase resolution.To address this problem,we use the first arrival to “demodulate” the wave field in the frequency domain with a goal of restoring the phase of wave field.Then we minimize an objective function consisting of so called “demodulated” wave field to solve wave equation inversion problem.In this way,we find that the inversion is much improved,and when the velocity perturbation in a complicated model reaches 35%,we can still obtain a good inversion.A computer simulation shows that our method is very robust for acoustical wave inversion with good reconstruction precision.

traveltime,non-linear inversion,phase,crosswell,objective function

1 Introduction

The paper is organized as follows:the problem of wave equation inversion method and its solution are described in the theory and method section.Then,we apply our method to the crosswell geometry to conduct a forward and inverse simulation.We compare the inversion results using the new method and old inversion method in the numerical test section.We find that a complicated model with 35% velocity perturbation can be reconstructed very well by our new method while standard nonlinear inversion method in frequency domain has failed.We believe that the method we propose here will be useful when applied to real data.The general idea proposed in this paper can be extended to inversion in the time domain case.

2 Theory and method of wave equation inversion with phase correction in baseband

Let us revisit the general inversion method in the frequency domain and check its solution first.We know that the goal in the non-linear inversion is to minimize the objective function:

(1)

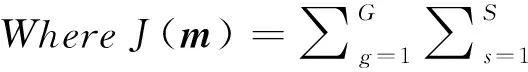
Figure 1 A time domain signal u(t)

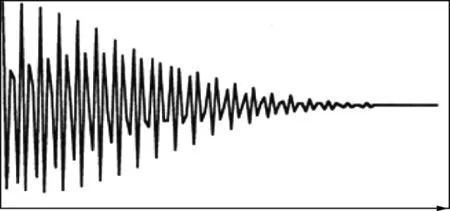
Figure 2 The real part of the spectrum of u(t)

Figure 3 The time domain signal of u(t+t0)

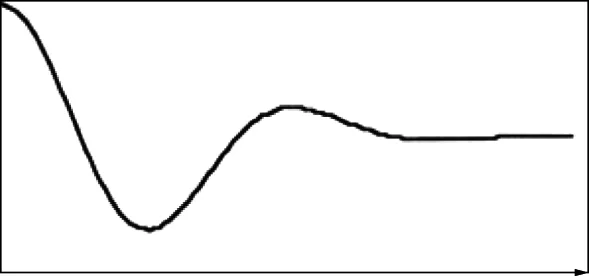
Figure 4 The real part of spectrum of u(t+t0)

as shown in figure 2.So we believe that the non-linear problem in the demodulated domain easier than before.

Therefore,we have the suggestion that the inversion will be better inversion by matching the demodulated waveform rather than the original waveform.According to nonlinear inversion theory,we establish a new object function as follows:

Q(m)=J(m)+αH(m)

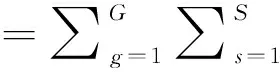
αH(m)→min

(2)

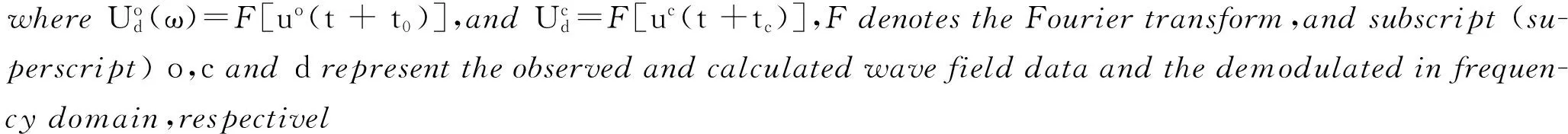
(3)

Therefore,byusingtheiterativeinversionshownbelowtoinvertformodelm(r),we have:

Where:

(6)

and from equation (2),we have:

(7)

(8)

From equation (3),we have:

(9)

where Δsiis the area ofi-th pixel and (∂tc)/(∂mi)can be derived by variable methods.Under the ray approximation,we have:

(10)

Where ΔliandViare ray length and velocity ini-th cell.The coefficientsxi(1≤i≤3) can be derived by the method described in the paper[5].

From equation (7),we see that there are two derivatives making contribution to the Fréchet derivative of object function,one is the derivative of first arrival to the model,another is the derivative of total field to the model.Therefore,the phase of first arrival is used as an implicit constraint condition which should be matched in all iterative steps,that is,the variation of the first arrival phase is also employed to correct the current model.Thus,this will be helpful for the iterative procedure to be convergent to the true model.So the inversion steps can be summarized as follows:

1) pick the first arrival time from the scattering waveformu(t);

2) shift the waveformu(t+t0);

4) calculate searching directionse1,e2,e3;

5) update the model using equation (4);

6) ifQ(m)≤ε,stop iterative inversion,otherwise,go to 4).

3 Inversion results using simulation data

Figure 5 and figure 6 are two synthetic models.In figure 5,there is a two layer perturbation.Figure 6 is a more complicated 2D model.The velocity in each region is shown.The minimum velocity is 5000m/s,the maximum 6750m/s,and the range of the variation is 35%.In the forward calculation,the image region is divided into 20×50 pixels,where

Figure 5 Layer Model

the width of each pixel is 2.5m.In the frequency we use is 200Hz.The experiment consists of 50 sources and receivers spaced at intervals of 2.5m apart.We use moment method to produce the observed wave field.Figure 7 and figure 8 are the tomography reconstruction results of the model (5) by the baseband demodulation method presented herein and the standard direct wavefield non-linear inversion method[5]

Figure 6 2D complicated model

Figure 7 Velocity tomography of layer model by the baseband demodulated method

respectively.The starting models are constant with a velocity of 5000m/s.Figure 9 and figure 10 are the tomography reconstruction of the model (6) by the baseband demodulation method presented herein and the standard direct wavefield non-linear inver sion method,respectively,in which the starting models are also constant with a velocity of 5000m/s.

Figure 8 Velocity tomography of layer model by direct wavefield non-linear inversion method

Figure 9 Velocity tomography of 2D complicated model by the baseband demodulated method

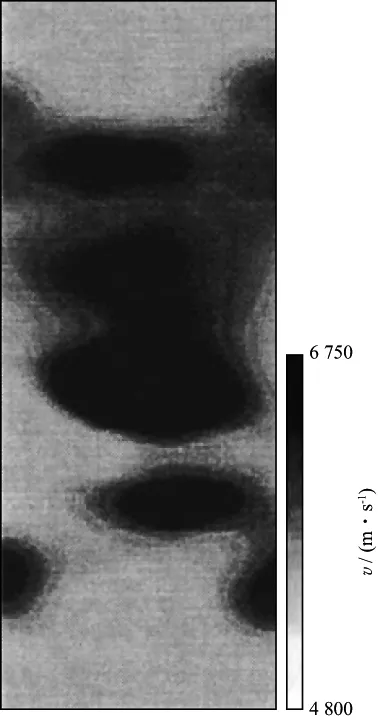
Figure 10 Velocity tomography of 2D complicated model by the direct wavefield non-linear inversion method

4 Conclusions

We put forward a new wave equation iterative tomography method,in which the first arrival traveltime is used to “demodulate” the wave field in frequency domain to reach the goal of resolving the large phase mismatch between the observed and calculated wave fields.Then the velocity is inverted by minimizing a new objective function which describes the mismatch between the observed “demodulated” wave field and corresponding calculated data below a threshold determined by the errors in the observation.In addition,in our algorithm,the first arrival phase is automatically used as an implicit constraint condition to help the algorithm to be convergent to the true model.Through this way,we can avoid the ambiguity problem of the phase between the observed and calculated wave field and obtain a robust wave equation inversion method.The computer simulation results show that when the perturbation of the velocity is as large as 35%,our inversion method still works while the old nonlinear inversion has already failed.

Acknowledgments The work was supported by the Seismic Tomography Project of Stanford University,a research consortium sponsored by companies of the oil and gas industry.The first author would like to thank Youli Quan for some useful discussion with him and Mark Van Shaack and Jesse Costa for their help in calculating the first arrival in the waveform.

[1] HARRIS J M.Diffraction tomography with arrays of discrete source and receivers[J].IEEE Transactions on Geoscience & Remote Sensing,1987,GE-25(4):448-455

[2] HARRIS J M,WANG G Y.Diffraction tomography in a layered background medium[J].Expanded Abstracts of 63rdAnnual Internat SEG Mtg,1993:49-52

[3] WU R S,TOKSOZ M N.Diffraction tomography and multisource holography applied to seismic imaging[J].Geophysics,1987,52(1):11-25

[4] PRATT R G,WORTHINGTON M H.Inverse theory applied to multi-source cross-hole tomography,part 1:acoustical wave equation method[J].Geophysical Prospecting,1990,38(3):287-310

[5] HARRIS J M,YIN F.Nonlinear multi-frequency wave equation tomography[J].Expanded Abstracts of 63rdAnnual Internat SEG Mtg,1993:988-991

[6] LUO Y,SCHUSTER G T.Wave equation traveltime plus waveform inversion[J].Expanded Abstracts of 60thAnnual Internat SEG Mtg,1990:1223-1225

[7] TARANTOLA A,CRASE E,JERVIS M,et al.Nonlinear inversion of seismogram,state of the art[J].Expanded Abstracts of 60thAnnual Internat SEG Mtg,1990:1193-1198

(编辑：顾石庆)

2016-11-04;改回日期：2016-12-06。

YIN Feng (1959 —),Lead engineer GE Healthcare.

P631

A

1000-1441(2017)01-0069-06

10.3969/j.issn.1000-1441.2017.01.008