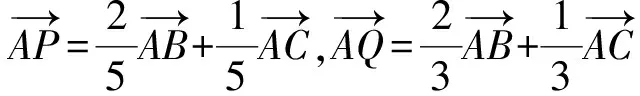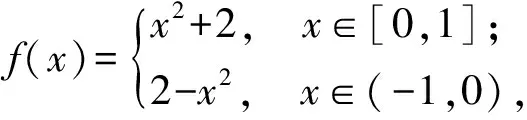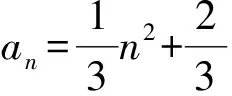数学创新题求解策略
——以概念型、定义型、开放型、建模型为例*
2017-03-15何豪明衢州高级中学何数思维工作室浙江衢州324006
●何豪明 (衢州高级中学何数思维工作室 浙江衢州 324006)
●张金良 (浙江省教育厅教研室 浙江杭州 310012)
数学创新题求解策略
——以概念型、定义型、开放型、建模型为例*
●何豪明 (衢州高级中学何数思维工作室 浙江衢州 324006)
●张金良 (浙江省教育厅教研室 浙江杭州 310012)
创新是以新思维、新发明和新描述为特征的一种概念化过程,原意有3层含义:第一是更新;第二是创造新的东西;第三是改变.数学创新能力一般是指对已经掌握的研究问题的方法、分析问题的思想和解决问题的途径进行推广和拓展,对未来的数学领域通过探索得到新的结果的能力.文章通过对概念型、定义型、开放型、建模型等数学创新题的探究,为数学创新题提供一般性的思维方法和解题策略.
数学创新题;概念型;定义型;开放型;建模型
创新是以新思维、新发明和新描述为特征的一种概念化过程.起源于拉丁语,它原意有3层含义:第一是更新;第二是创造新的东西;第三是改变.创新是人类特有的认识能力和实践能力,是人类主观能动性的高级表现形式,是推动民族进步和社会发展的不竭动力.
数学创新能力一般是指对已经掌握的研究问题的方法、分析问题的思想和解决问题的途径进行推广和拓展,对未来的数学领域通过探索得到新的结果的能力.
数学创新题一直是高考命题的重点,特别是概念型、定义型、开放型、建模型等数学创新试题,它们解法灵活,同时具有一定的探索性,尤其值得关注.
1 概念型
概念型信息题是指人类在认识过程中,把所感觉到的事物的共同特点抽出来,加以概括,成为概念.概念是人脑反映客观事物根本属性的思维形式.其目的是为了考查学生独立获取信息、加工信息的学习能力.因而解决此类问题的关键是仔细阅读、抓住信息、透彻理解.
概念型信息题的高考命题特点是对“反映客观事物根本属性的思维形式”的考查,如2016年全国数学高考理科试题卷Ⅰ第7题等;或考查学生对教材中已经学习过的概念的理解和应用能力,如2015年浙江省数学高考理科试题第7题等.
概念型信息题的复习重点是对事物共同特点的抽象概括能力、总结规律的能力和不同数学语言相互翻译的能力.
例1 已知定义域为(0,+∞)的单调函数f(x),满足对任意的x∈(0,+∞),都有f[f(x)-log2x]=6,求函数f(x)的解析式.
分析 因为对任意的x∈(0,+∞),都有
f[f(x)-log2x]=6,
又f(x)是定义在(0,+∞)上的单调函数,所以利用函数单调性的定义可以得到f(x)-log2x为定值(揭示函数单调性概念的内涵).设t=f(x)-log2x,即
f(x)=t+log2x,
从而
f(t)=t+log2t.
又因为f(t)=6,所以
6=t+log2t,
解得t=4,故所求函数的解析式是
f(x)=4+log2x(其中x>0).
2 定义型
定义型应用题通过指出定义所反映的事物本质特征来明确定义的内涵和外延,它科学地揭示了客观世界中事物的本质特征.定义是一种人为的广泛、通用的解释意义.而对自定义型问题,则要求学生从新的定义、方法到新规则的学习,在较短时间内获取信息、对信息进行加工处理.它有利于提高学生主动获取信息、加工信息的能力.解决此类问题的关键是要用数学的文字语言、符号语言和图形语言理解定义、熟悉定义,从而掌握定义.
定义型应用题或给出新的定义,考查学生对新定义的理解和应用能力,如2016年全国数学高考理科卷Ⅲ第12题、2016年浙江省数学高考理科试题第18题等.
定义型应用题的复习重点是深刻理解各种数学定义,熟练掌握定义的不同数学语言的相互理解和转换.


3 开放型
所谓开放型问题,是相对于中学课本中有明确条件和明确结论的封闭型问题而言的.开放性探究题可分为条件开放型问题、结论开放型问题和条件结论均开放的全开放型问题.对于具有多重结果的结论开放型问题,应抓住条件中那些影响结论的动态因素(如定义、公式的特定条件、几何体的不同形态等),或分类讨论,或构造不同图形,全面考查问题的各个方面.对于只给出一个特定情境,而命题的条件、结论及推理判断过程均不确定的开放型试题,应该灵活运用数学知识,回顾相近或相似的题型、结论、方法,进行类比猜想,在给定的情境中自己去假设、求解、调整方法、确定结果.
开放型问题或对于只给出一个特定情境而命题的条件、结论及推理判断过程均不确定的开放型试题的考查,如2016年四川省数学高考理科试题第15题等;对条件开放或结论开放型问题的考查,如2015年安徽省数学高考理科试题第15题、2015年全国数学高考理科卷Ⅱ第20题等.
开放型问题的复习重点是对开放性探究题的条件或结论的探究,或对只给出一个特定情境而命题的条件、结论及推理判断过程均不确定的开放型试题的探究.
例3 设α,β是2个不同的平面,m,n是平面α及β之外的2条不同的直线,给出4个论断:1)m⊥n;2)α⊥β;3)n⊥β;4)m⊥α.以其中3个论断作为条件,余下的一个论断作为结论,写出你认为正确的一个命题.
分析 求解条件、结论均开放型的试题,要先组成命题,然后通过代数运算或逻辑推理去验证真假.求解这类试题,没有现成的公式可套,需要学生自己去探索.本题可以组成4个命题,逐一判断,得到的答案是:m⊥α,n⊥β,α⊥β⇒m⊥n或m⊥n,m⊥α,n⊥β⇒α⊥β.
4 建模型
建模型应用题是指能反映特定问题或特定具体事物、具体系统内部的数学关系式结构.它或能解释特定抽象的现实状态,或能预测对象的未来状态,或能提供处理对象的最优决策或控制.此类题要求学生会数学地提出问题、分析问题,并能综合运用所学的知识和技能解决问题,形成解决问题的一些基本策略,其解题的总体思路是:读题—建模—解模—得解.
建模型应用题是对给出现实生活中的一个事例,要求学生把它抽象为数学问题,即通过建立数学模型来解决,如2016年全国数学高考理科卷Ⅰ第4题、2015年全国数学高考理科卷Ⅱ第12题等.
建模型应用题的复习重点是如何把实际问题转化为数学问题的能力以及对不同模型的识别能力.
例4 已知f(x)为定义在(-∞,+∞)上的可导函数,且f(x) ( ) A.f(1)>e·f(0),f(2 012)>e2 012·f(0) B.f(1) C.f(1)>e·f(0),f(2 012) D.f(1) F′(x)=-e-x[f(x)-f′(x)]>0, 得到F(x)是R上的增函数,即 故选A. 2)正四面体A-BCD的棱长为1,棱AB∥平面α,求正四面体上的所有点在平面α内射影构成的图形面积的取值范围. 3)已知棱长为a的正四面体可以在一个单位正方体(棱长为1)内任意地转动.设P,Q分别是正四面体与正方体的任意一个顶点,当a达到最大值时,求点P,Q间距离的最小值. 分析 研究正四面体问题,感受数学的对称美,可以考虑以正方体为模型进行思考,产生如下解法: 图1 图2 ( ) 2.已知y=f(x)(其中x∈R)的导函数为f ′(x).若f(x)-f(-x)=2x3,且当x≥0时,f ′(x)>3x2,则不等式f(x)-f(x-1)>3x2-3x+1的解集是 ( ) 4.(x2-x+y)5的展开式中x3y2项的系数等于______(用数字作答). 5.过抛物线C:y2=4x的焦点F作直线l交抛物线C于点A,B,若|AF|=3|BF|,则直线l的斜率是______. 6.一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的______(填入所有可能的几何体前的编号).①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱 7.在直四棱柱ABCD-A1B1C1D1中,当底面四边形ABCD满足条件______时,有A1C⊥B1D1(填上你认为正确的一种条件即可,不必考虑所有可能的情形). 8.已知某几何体的主视图、俯视图、侧视图均为等腰直角三角形,如果直角三角形的直角边长均为2,那么这个几何体的表面积可能为______(结论开放题). 9.在数列{an}中,已知a1=1,a2=2,请写出该数列的4个通项公式,他们分别为______;______;______;______. 11.若对任意的x∈D,均有f1(x)≤f(x)≤f2(x)成立,则称函数f(x)为函数f1(x)到函数f2(x)在区间D上的“折中函数”.已知函数f(x)=(k-1)x-1,g(x)=0,h(x)=(x+1)lnx,且f(x)是g(x)到h(x)在区间[1,2e]上的“折中函数”,则实数k的值是______. 1)请你给出a,b的一组值,使直线l和椭圆C相交. 2)当直线l和椭圆C相交时,a,b应满足什么关系? 3)若a+b=1,试判断直线l和椭圆C的位置关系. 4)请你在第3)小题的基础上添加一个合适的条件,求出直线l的方程. 参 考 答 案 6.①②③⑤ 7.AC⊥BD或四边形ABCD是正方形或四边形ABCD是菱形等. 9.等差数列形式:an=n(其中n∈N*); 等比数列形式:an=2n-1(其中n∈N*); 等和数列或等积数列形式: 三次函数形式(待定系数法):an=n3+n2-9n+8(其中n∈N*)或an=n3-2n2+2(其中n∈N*)等. 13.1)取a=1,b=0,则直线l:y=x和椭圆C相交. (1+2a2)x2+4abx+2b2-4=0. 因为直线l和椭圆C相交,所以由Δ>0可得b2-4a2-2<0. 3)因为a+b=1,所以b=1-a,从而 y=ax+1-a, 即 y-1=a(x-1), 故直线l恒过点(1,1). 4)添加条件:直线l过点(2,0),则a=-1,因此直线l的方程为x+y-2=0. ��2016-12-22; 2017-01-25 何豪明(1967-),男,浙江衢州人,中学高级教师.研究方向:数学教育. O12 A 1003-6407(2017)03-31-04
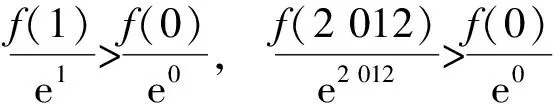



5 精题集萃