裂隙岩体裂隙面随机分布模型研究
2017-03-15仲云飞李磊
仲云飞+李磊
摘要:大量存在于岩体中的裂隙具有随机分布的特点,在野外调查的基础上获得的裂隙分布参数的处理一直是地质工程中的难点问题。虽然裂隙是随机分布的,但是在统计学上服从一定的分布函数。本文通过统计学方法,建立了裂隙的统计模型,并依托实际工程提取对工程岩体的力学行为具有控制性作用的裂隙参数,建立了反映裂隙随机分布规律的统计模型。
关键词:岩体;裂隙面;随机分布;概率图;统计模型
1.前言
岩体是一种不连续介质,各种不同成因的结构面相互交切、组合形成了特定的岩体结构。结构面的几何参数通常指某组结构面的产状、迹长、间距、闭合度等等。这些几何参数决定了岩体被这些结构面切割的特征,岩体内部的各种不同方向、规模、形态的地质界面往往对岩石地基工程起控制性作用,是研究工程岩体结构的重要参数。在平硐、钻孔和露头面上可以获得有关结构面几何参数的大量资料,如果通过这些资料可以总结出岩体结构面参数的数理统计特征(某种概率的密度函数分布)和统计参数(裂隙参数的均值和标准差),就可以为损伤力学、随机有限元、离散元和块体理论等岩体力学边缘学科提供基础资料。
在野外测量的大量结构面的几何参数往往带有不确定性、不完整性以及随机性等特点,如何对这些大量的资料进行处理以并得到结构面几何参数分布的规律是研究结构面对岩体力学性质的影响所要做的首要工作。在大量的实践和统计结果表明裂隙岩体的结构面大体上遵循若干特定的曲线,其统计的概率密度均具有随机的特征[1,2]。本文通过建立结构面分布的随机模型,分析了某核电站核岛区基岩中裂隙的分布规律,为后续评价基岩的岩土力学性质提供了基础资料。
2. 概率图法
科研及工程人员研究表明,在描述岩体结构面的几何参数分布时,主要有均匀分布、负指数分布、正态分布和对数正态分布四种[3,4]。对于某一组特定的样本资料,关键问题是如何在上述四种已知概率密度函数中选用正确的函数描述。
设统计了某一组N个资料x1, x2,??xn选用了某一概率分布函数F(x)。首先将x1, x2,??xn按其顺序排队,为θ1,θ2,??θn,那么,相应θi的分布函数从理论上讲,应为F(θn)=i/N,为了避免出现在i=N时F(θn)=1的不合理现象,定义经验分布函数值为:
以θi为横坐标,θt为纵坐标,可以将N个数据点绘制在该坐标中。从理论上讲,该N个点应连成一个与横坐标轴夹角45°通过原点的直线。但如果在实际采集数据并分析时,如果该N个点大致沿一条直线分布,那么不论截距和斜率大小,都可以认为该组资料符合所选用的分布函数F(x)。
由于正态分布函数(对数正态分布函数可以转换为正态分布函数来考虑)没有解析式,其反函数难以用显式给出,在计算θt时,可采用下列近似方法计算:
首先将非标准正态分布函数转换成标准正态分布函数,其密度函数为:
4 某核岛基岩裂隙分布
某核电站核岛由1#和2#两部分组成,各建(构)筑物子项包括核反应堆厂房、核服务厂房、以及控制厂房等,为该核电站的核心建筑,任何失灵、损坏均有有可能会导致安全事故,造成巨大的经济损失并造成不良的社会影响,因此,在勘察设计前期,应当查明核心建筑分布区的基岩裂隙分布规律,进一步为后续承载力、稳定性等各方面评价提供基础资料。
据区域地质资料及前期勘察资料,核岛建筑物地段无断裂构造通过,主要构造线为NE、NW走向的两组裂隙,此外还包括有大型裂隙、裂隙密集带。
①随机分布裂隙
经现场调查、测绘查明该核岛地基岩体中主要发育两组裂隙:第Ⅰ组.走向NE,倾向NW,倾角为45°的裂隙;第Ⅱ组.走向NW,倾向NE,倾角75°。裂隙间距一般均大于0.4m,裂隙面平直,一般胶结闭和较好,部分张开宽度1- 3mm,个别达10mm,充填有高岭土、蒙脱石等粘土矿物。
②规模较大的裂隙
分布在1#核岛东侧临海岸线一侧,张开宽度0.1~0.6m,延伸长度一般大于25m,上宽下窄,往深部、陆地方向逐渐闭和,充填有块石、碎石、砂、贝壳等。
③裂隙密集带
主要分布在1#核岛东侧海岸线一带,主要由NW走向的一组裂隙密集形成,少数由NE走向60~80°一组形成,一般裂隙间距10~30cm,延伸长度20m左右,带宽2~7m不等。2#核岛地段没有分布。
根据已有的勘察资料并结合现场调查,对核岛区的主要裂隙进行了统计分析,将核岛区的裂隙分为两组:Ⅰ组:走向NW组;Ⅱ组:走向NE组,同时还存在少量的绿泥石片岩与围岩的软弱接触面,由于软弱接触面的统计资料较少,所以根据勘察报告提供的参数。采用概率图法来确定各组裂隙几何参数的概率密度函数,检验结果见表1, 2。
由表1、2可知:Ⅰ组裂隙的倾向服从正态分布,倾角服从对数正态分布,迹长和间距服从负指数分布;Ⅱ组裂隙倾向服从对数正态分布,倾角服从均匀分布,迹长服从对数正态分布,间距服从负指数分布。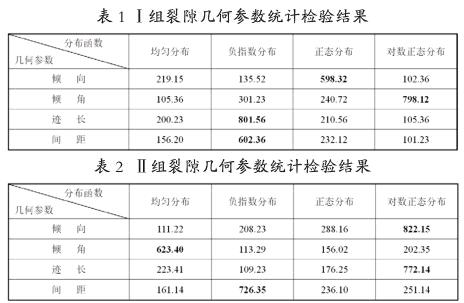
确定了裂隙几何参数的概率分布形式后通过最小二乘法对裂隙几何参数的均值和方差进行计算,计算的结果见表3、4。

5 結论
(1)可靠的概化地质模型是进行岩体力学计算的前提条件,特别是裂隙岩体,除了其岩性组合特征以外,最关键的是查清裂隙的分布组合情况。本文以野外地质调查为基础,在野外裂隙实测资料的基础上进行统计分析,建立了能够客观反映裂隙实际分布状况的统计模型,提取了力学分析中具有关键作用的裂隙参数。
(2)统计分析方法对于处理大量具有随机性的裂隙统计参数具有较好的实用性,能够提取出代表性的裂隙参数,可以有效避免对大量统计数据取平均值带来的不确定性因素的影响。
(3)在后续研究中,应当开展根据关键统计参数进行裂隙随机可视化模型的研究工作,以提供更为直观可靠的统计规律。
参考文献
[1]Prest S. D. And Hudson J. A., Discontinuity Spacings in Rock, Inter. J. Rock Mech. Min. Sci. and Geomech. Abstr., 1976, 13
[2]汪小刚,陈祖煜,《岩体结构面调查统计和计算机模拟分析及其在漫湾电站左岸边坡稳定分析中的应用》,水利水电科学研究院,1991
[3] 于本昌,《基于蒙特卡罗随机裂隙的岩溶水工隧洞稳定性及渗流特性研究》2015
[4]许湘华 曲广琇方理刚《基于节理几何参数不确定性的边坡可靠度分析》2015
[5] 陈昌平,《节理岩体结构定量化研究》,第一届全国大坝岩体力学讨论会暨第三届岩石力学与工程学会岩体物理数值模拟讨论会,1993
