General Integral Formulas of(0,q)(q>0)Differential Forms on the Analytic Varieties
2017-03-14
(School of Mathematical Sciences,Xiamen University,Xiamen 361005,Fujian,China)
§1.Introduction
Let∆be a holomorphic domain inCn,we consider the following bounded domain⊂∆.We assume that the boundary∂D(here and for the rest of this paper we always assume that∂Dis piecewise smooth)of a bounded domainDin spaceC(n)consists of a chain of slit spaces,and∂Dcan be expressed as
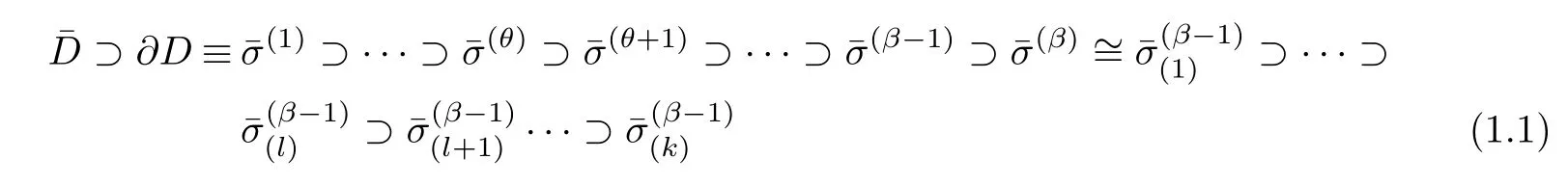

Hatiziafratis[2]obtained an explicit Koppelman type integral formula for the bounded domain with smooth boundary in analytic varieties.On the analytic varieties,in order to get the integral representation formulas of(0,q)(q>0)differential forms must be used to get the integral representation formulas of(0,q)(q=0)differential forms(i.e.differentiable functions)with different methods.That we need to get the following lemma 2 and its corollary,as well as lemma 3.This present paper, firstly using different method and technique we derive the corresponding integral representation formulas of(0,q)(q>0)differential forms for the two types of the bounded domains in complex submanifolds with codimension-mi.e.in the complexn−m(0≤m<n)dimensional analytic varieties.Secondly we obtain the unified integral representation formulas of(0,q)(q>0)differential forms for the general bounded domain in complex submanifolds with codimension-mi.e.in the complexn−m(0≤m<n)dimensional analytic varieties,which include Hatziafratis formula,i.e.Koppelman type integral formula for the bounded domain with smooth boundary in analytic varieties.In particular,whenm=0,we obtain the unified integral representation formulas of(0,q)(q>0)differential forms for general bounded domain inCn,which are the generalization and the embodiment of Koppelman-Leray formula.
We also note:(a)From the formulas of this paper is easy to get the solution of the¯∂-equation.And we can then consider solution estimation problem[7]of the described(To save space,this paper is not detailed).(b)The integral formulas of this paper can be used as a local results on Stein manifold,which can be extended to the Stein manifold.
§2.Some Lemmas

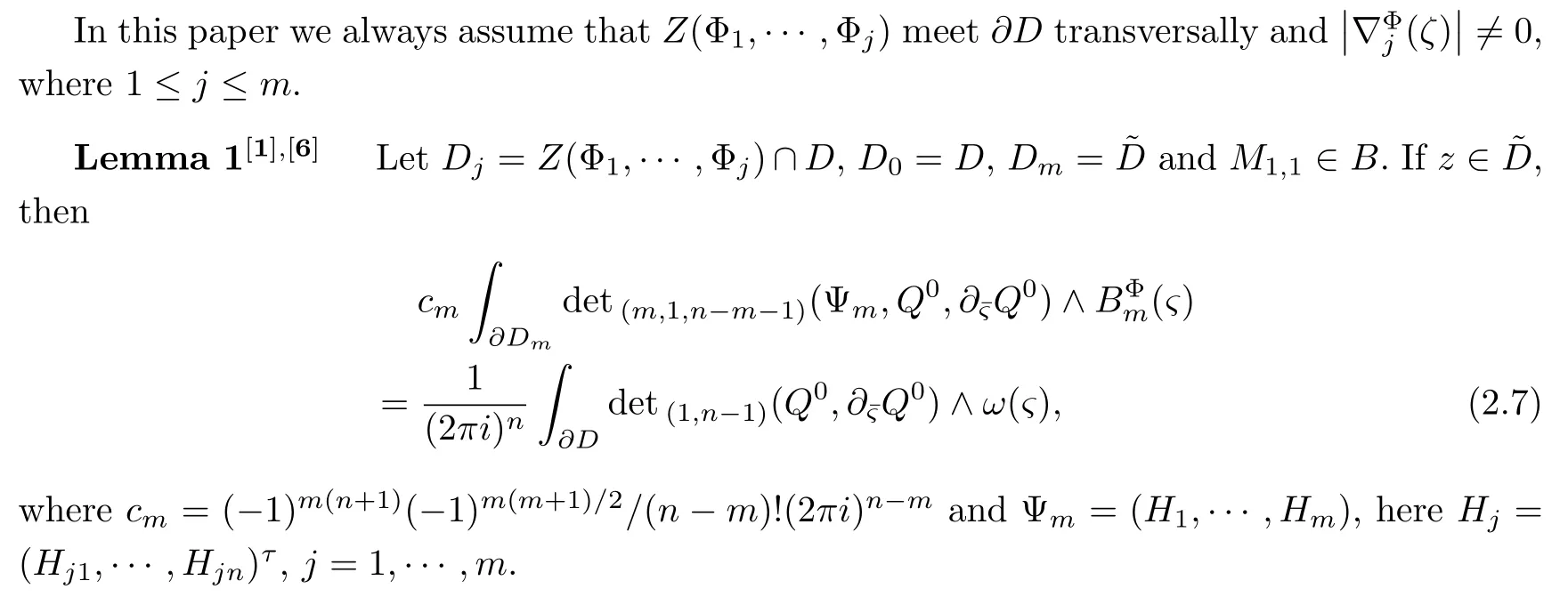


Becauseν(z)is arbitrary,by(2.11)we get the expression(2.10).
The papers of Hatziafratis[1-2]and the author[6]are most relevant referens to above lemmas.
§3.Main Theorems

Theorem 1IfDis a bounded domain with piecewise smooth boundaries inC(n),then for(0,q)(q>0)differential formu(z)on¯Dandz∈˜D,we have the extension of the Koppelman-Leray formula on the complex submanifolds i.e.on the complexn−m(0≤m<n)dimensional analytic varieties
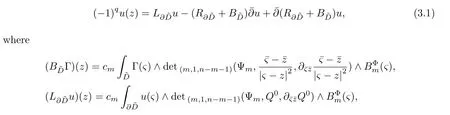

Lettingr→0 and taking the limits of the two side of(3.3),by lemma 3 we get(3.1).
Remark 1Using the properties of the determinant,which includes the exterior differential forms(cf.[4]),and Laplace theorem of the determinant,Hatziafratis formula[2]can be easily obtained from the theorem 1(only justQ0=/|ς−z|2).
Theorem 2Let the boundary∂Dof a bounded domainDinC(n)be defined by(1.1),and∂be defined by(1.4)(wherek=1).Letτm=B0∩Z(Φ1,···,Φm)and∂τm=ε0(β),and=∂(Λ(β−1)×τm).Assuming thatis a chain,withand∂as the boundary chain,then for the(0,q)(q>0)differential formu(z)onandz∈,we have the integral representation on the complex submanifolds for the bounded domain of the II-type−


Therefore,we have
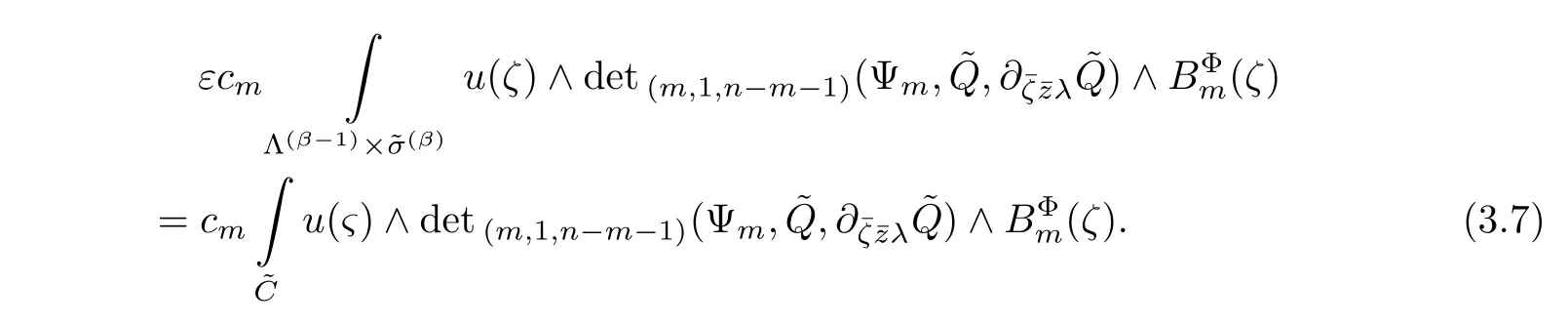
On the other hand,since
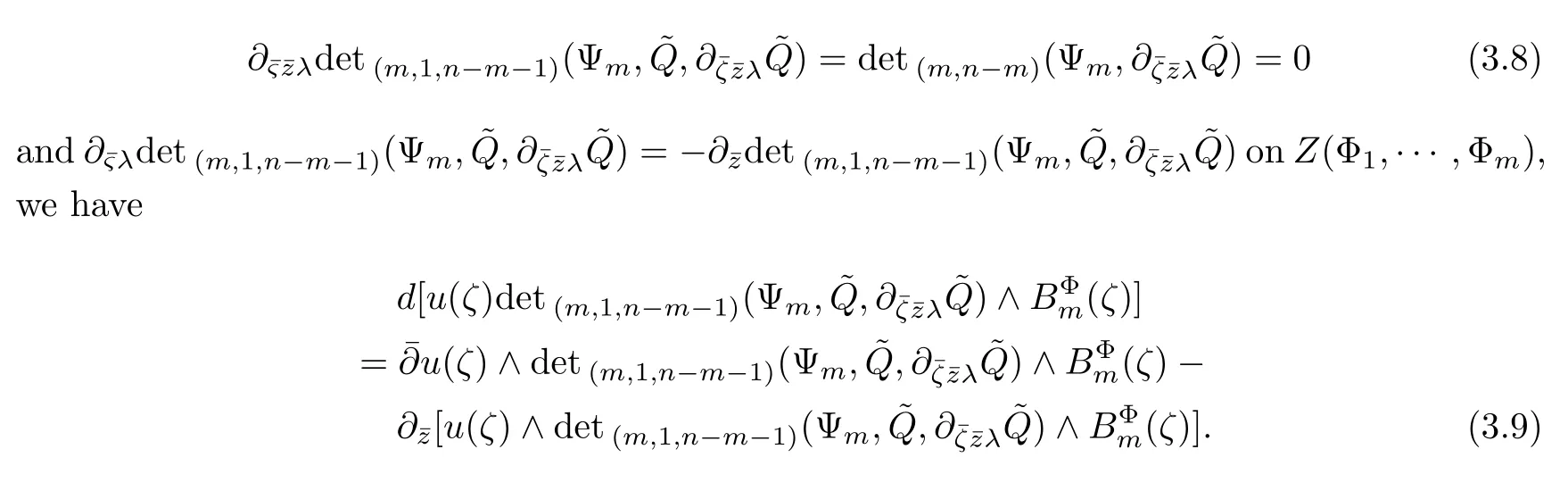

It is derived from(3.7)and(3.10)that

By(3.11)and(3.1)we obtain(3.4).
Assume thatDis a bounded domain and the boundary∂DofDcan be represented aswhereqji(ς,z)are holomorphic in(ς,z)∈∂D×DandFj(ς,z)/=0 atς∈σjfor any fixedz∈D.Then we denoteFj(ς,z)∈A.

Theorem 3Let the boundary∂Dof a bounded domainDinC(n)be defined by(1.1),and∂be defined by(1.4),then for the(0,q)(q>0)differential formu(z)onandz∈we have


Then by(3.1 8),(3.1 9)and Stokes formula we have

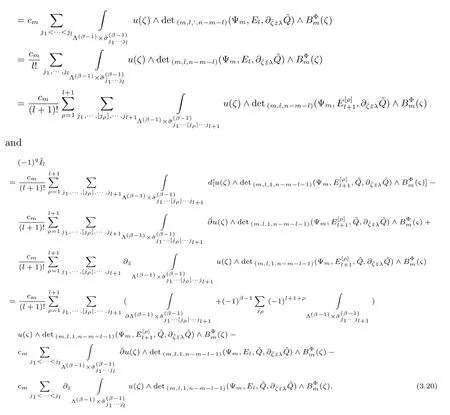
Taking it in to account that
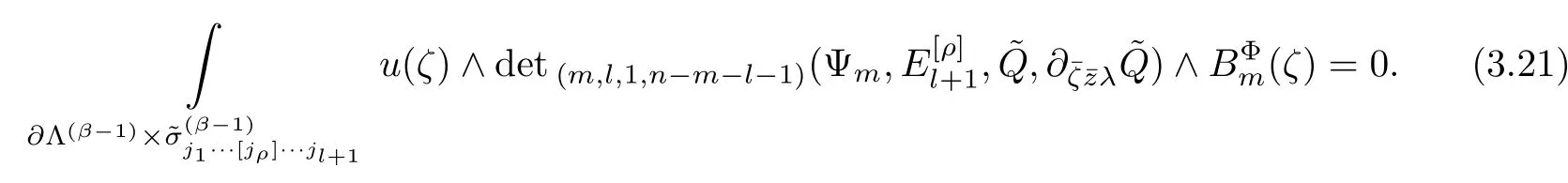
From(3.2 0),(3.2 1)and(3.1 3)we obtain


wherel=1,2,···,k−1.
Using(3.22)repeatedly,we obtain

By(3.14),we have
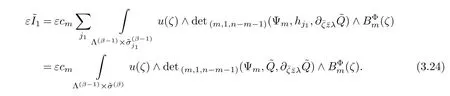
It is follows from(3.23),(3.24)and(3.4)that(3.15).
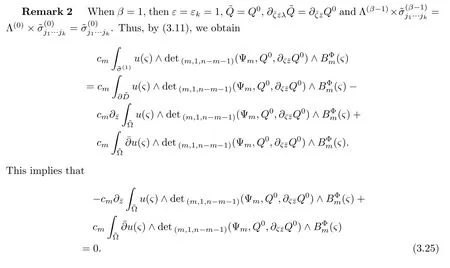
Thus whenβ=1,taking account of(3.25),then(3.15)translates into

which is the integral representation of the(0,q)(q>0)differential forms on the complex submanifolds for the bounded domainDof I-type.
Theorem 4Let the boundary∂Dof a bounded domainDinC(n)be defined by(1.1),and∂be defined by(1.4),then for the(0,q)(q>0)differential formu(z)onandz∈,we have the following formulas:(a)Whenl>1,


Thus,we have

By(3.31),we have

whered=∂ς+∂¯ς+dλ+dµ.
For the sake of simplicity,

is denoted byX,Y,Zrespectively,then∂X=Y+Z−Stokes formula we have

By computing we obtain the left hand side of(3.33)=0.
This implies that

Especially,whenl=1,by(3.35)we have

Thus whenl>1,it is derived from(3.35)and(3.15)(wherelis used insteadk)that(3.27).Whenl=1,it is derived from(3.36)and(3.4)that(3.28).
Remark 3Whenl=k>1,thenT=.Thus(3.27)translates into(3.15).In particular,whenl=k=1,then(3.18)translates into(3.4).
Remark 4Whenl=k>1 andβ=1,we haveT==Q0and(3.27)translates into that(3.26).
It is derived from remark 3 and remark 4 that(3.27)and(3.28)are the unified integral representations of(3.4),(3.15)and(3.26).
Remark 5Whenm=0,then(ζ)=(ζ)=n!ω(ζ),Ω and∂=∂D,which is defined by(1.1).From above formulas we can obtain the unified integral formulas of the(0,q)(q¿0)differential forms for the bounded domain inCn,i.e.we have the following results:
(a)By(3.1),we have Koppelman-Leray formula

where
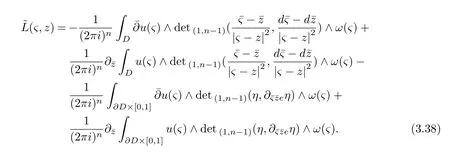
(b)By(3.4),we have

which is an extension and an embodiment of Koppelman-Leray formula.
(c)By(3.26),we have

which is an extension and an embodiment of Koppelman-Leray formula.
(d)By(3.27)and(3.28),we have respectively:
Forl>1,


where

(3.41)and(3.42)are the unified integral formulas of(3.37),(3.39)and(3.40),and make Koppelman-Leray formula generalize and embody.
[1]HATZIAFRATIS T E.Integral representation formulas on analytic varieties[J].Pacific J Math,1986,123:71-91.
[2]HATZIAFRATIS T E.An explicit Koppelman type integral representation for muls on analytic varieties[J].Michigan Math J,1986,33:335-341.
[3]φVRELID V.Integral representation formulas andestimates forequation[J].University of Math Scund,197129:137-160.
[4]SOMMER F.Ueber die Integralformeln in der Funktionentheorie mehrerer Komplexer Veranderlichen[J].Math Ann,1952,125:172-182.
[5]RANGE R M,SIU Y T.Uniform extimates for the-equation on domains with piecewise smooth strictly pseudoconvex boundaries[J].Math Ann,1973,206:325-3.
[6]CHEN Shujin.General integral representation of holomorphic functions on the analytic subvariety[J].Publ RIMS Kyoto Univ,1993,29:511-533.
[7]RANGE R M.A pointwise A-prori estimate for theNeumann problem on pseudoconvex domains[J].Pacific J Math,2015 275:409-432.
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- Local Existence of Solution to the Incompressible Oldroyd Model Equations
- A Finite Volume Unstructured Mesh Method for Fractional-in-space Allen-Cahn Equation
- The 1-Good-neighbor Connectivity and Diagnosability of Locally Twisted Cubes
- Adjacent Vertex Distinguishing I-total Coloring of Outerplanar Graphs
- Recover Implied Volatility in Short-term Interest Rate Model
- Convergence Rate of Estimator for Nonparametric Regression Model under-mixing Errors
