基于X波段海洋雷达的风浪联合反演方法研究

邱吉东，张 彪，陈忠彪，何宜军

（南京信息工程大学 海洋科学学院，江苏 南京 210044）

基于X波段海洋雷达的风浪联合反演方法研究

邱吉东，张 彪，陈忠彪，何宜军

（南京信息工程大学 海洋科学学院，江苏 南京 210044）

提出了一种新的利用X波段海洋雷达联合反演海面风速与海浪谱的方法，该方法不需要额外的信息输入来反演海浪谱。通过利用风速与雷达后向散射强度的经验关系获得海表风速，然后将反演的风速输入风浪谱，通过求解该模拟风浪谱与雷达观测图像谱的约束函数的最小值来确定海浪谱。利用实验数据对反演方法进行了验证，风速、有效波高、主波周期以及主波波向反演的均方根误差分别为1.9m/s，0.4m，1.2 s和9.6°,证明了该方法的可行性。

X波段海洋雷达；风速；海浪谱；联合反演

X波段海洋雷达被应用于海表物理参数反演已经有近半个世纪的历史。从1965年Wright从 X波段雷达图像直接进行海浪传播方向和波长的判读[1]，到1983年，Ziemer和Rosenthal对雷达图像应用二维傅里叶变换获得海浪波数谱[2]，并利用波数谱估算了海浪参数，再到Young提出对雷达图像序列进行三维傅立叶变换[3]，利用X波段雷达海浪反演方法一直在不断进步。

本世纪初X波段雷达在风速反演方面上取得了飞速的发展，Heiko Dankert等提出利用神经网络算法和光流场算法估算风速和风向[4-5]；Lund等提出用最小二乘法拟合得到的风速与谐波函数的多项式关系[6-7]；Vicen-Bueno等建立了基于雷达图像灰度值的物理模型函数来反演风速[8]；W Huang提出基于谱分析的风速反演方法[9]。上述方法在风速和海浪的反演上都是单独反演，并且需要分别定标。

本文在现有研究的基础上提出了一种新的风速反演经验方程及风浪联合反演方法，只要在风速反演上进行定标，对海浪的反演不需要额外的定标。第二节将介绍风速和海浪谱的反演方法；第三节将给出反演方法的结果验证；最后对全文进行了总结与讨论。

1 反演方法介绍

1.1 风速的反演方法

首先对雷达图像序列I(θ,r,t)求平均

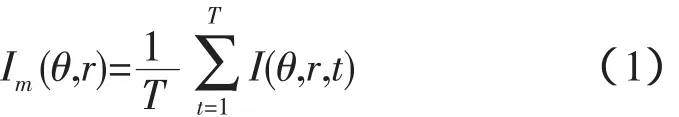
式中：T为雷达图像序列的时间总长度；θ为方位向；r为距离向；t为时间。

对雷达平均图像的每一方位向求和：

式中：M为单位方位向上图像元的总数。E反映了雷达回波能量在方位向上的总体水平。

将所有方位向上的E求平均得到S：

式中：Θ表示雷达图像的方位向总数；S反映了雷达图像序列的总体后向散射回波的水平[9]。

海面后向散射强度与风速存在一定的非线性关系[8，10]，经验的物理模型函数可以确定风速：

式中：a，b和c为待定系数；u10为海表10 m风速。通过拟合雷达图像序列总体散射值S与风速的关系，可以标定a，b和c来反演风速。

本文提出了新的经验物理模型函数来反演风速，具体形式如下：

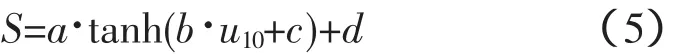
式中：a，b，c和d都是待定系数。

1.2 海浪的反演方法

1.2.1 海浪谱的数值仿真 本文中海浪频谱选用了JONSWAP谱[11-13]，其形式如下：

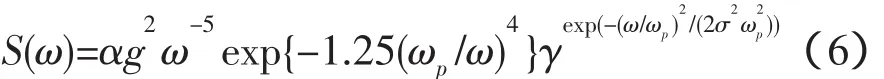
式中：g为重力加速度；ωp为谱峰频率；α为能量尺度参数，本文中取α=0.003；γ为谱升因子；σ为峰形参数；γ和σ分别由下式确定：

式中：cp为波动传播峰值速度。由于本研究试验资料在近岸地区获取，根据线性波动理论，在水深较浅的区域，波动传播速度由水深决定，cp=为重力加速度，h为水深。

实际海面是二维的，所以还应该考虑海浪能量在不同方向上的分布，这就需要引入方向谱。方向谱可以写出如下形式：

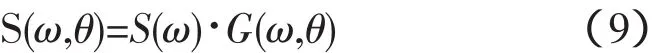
其中方向函数G(ω，θ)选用光易型方向函数:

式中：Γ为伽马函数；s为角扩散系数，与频率与风速有关：

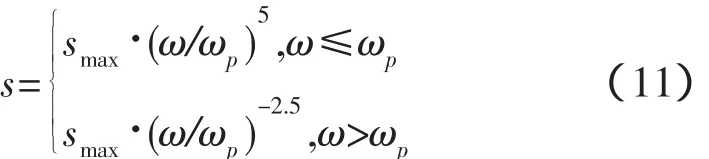
Goda建议的峰值角扩散系数smax如表1所示[14]：

表1 峰值角扩散系数smax取值表

1.2.2 雷达图像谱的提取 本文采用了Young等提出的利用傅里叶变换获取雷达图像谱的方法[3]。首先假定选择分析的波场具有平稳性的和各项同性，我们可以对其整个波场应用三维傅立叶变换。对雷达灰度序列图像I(x,y,t)三维傅立叶变换得到三维波数频率雷达图像谱f(kx,ky,ω)，即

雷达图像谱f(kx,ky,ω)的能量主要包括以下3部分：

(1)波浪成分，这部分能量占图像谱的主要部分；(2)由斑点噪声引起的背景噪声能量；

(3)高次谐波能量，这是由于雷达的非线性成像机制引起的。

之前的研究通过利用调制传递函数的方法提取海浪成分[15-17]，而调制传递函数又受到距离向、方位向的影响，单一的调制传递函数在反演海浪谱时具有一定的限制性，本文通过海浪谱仿真拟合的方法不需要利用到调制传递函数。

1.2.3 海浪谱的反演 海浪谱反演的流程图如下：

图1 海浪谱反演流程图

本文中的海浪谱仿真只与3个参数有关：(1)10m风速u10；(2)峰值波数kp；(3)波浪主波传播方向θp。10m风速可以通过反演得到，所以只需要确定峰值波数kp和波浪主波传播方向θp这两个变量就可以确定风浪谱。假设风浪在风向上是充分成长的，这一假设适用于大部分风浪占主导的情况，但在涌浪占主导的情况下会出现较大误差。所以在方向谱峰值角扩散系数Smax的选择上，本文使用了风浪情况下的Smax=10。

首先通过雷达图像序列反演得到风速和雷达图像谱，然后将归一化的仿真海浪谱和归一化雷达图像谱带入约束函数。由于需要通过约束函数确定最接近雷达观测图像谱的仿真海浪谱，所以约束函数中必须包括归一化的仿真海浪谱、归一化的雷达图像谱以及归一化的两谱之差，所以确定约束函数形式[18]如下：

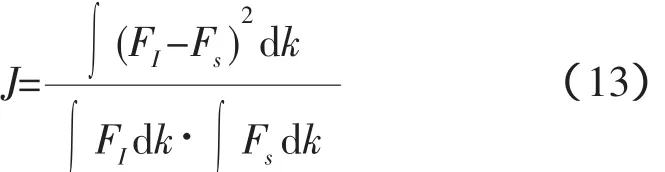
式中：FI为归一化雷达图像谱；Fs为归一化仿真海浪谱。

设定峰值波数kp的步长为0.001 rad/m，主波波向θp的步长为1°，通过迭代，求得J的最小值，其对应的kp和θp就是需要的结果。此时的仿真海浪谱即可认为是有效海浪谱。最后通过对海浪谱进行计算，可以得到有效波高Hs、主波波长λ和主波周期T等参数，如下所示：

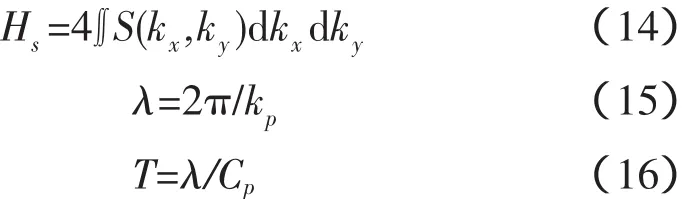
2 实验与结果

2.1 实验数据

为了验证反演算法及测试仪器的性能，我们于2015年1月在福建平潭岛进行了观测实验。平潭岛在台湾海峡以西，岛屿南北长29 km，东西宽19 km，是全国第五大岛。实验的时间在冬季，主要原因是这段时间寒潮的影响比较频繁，因而经常有高海况出现，风力最高可以达到25 m/s，风向常年以北风和东风为主。

本文实验所用的导航X雷达是基于日本FURUNO公司生产的船载导航X波段雷达改装而成。天线的水平波束宽度是1.2°，电磁波的中心频率是9.41GHz，对应的电磁波波长为3.19 cm，极化方式为VV极化。天线的转速是24 rot/min，即旋转周期为2.5 s，用本系统观测海浪时一般每组数据（即每个雷达图像序列）记录32幅雷达图像，所以共需要80 s。

图2为2015年1月15日17时00分所采集的图像序列中的一幅图像，其中黑框范围内为反演程序利用的256×256大小的数据区域，星号代表的是浮标所处位置。

图2 2015年1月15日17时00分雷达图像，黑框内为计算采样范围，星号为浮标位置

2.2 结果分析

2.2.1 风速的反演结果 本文对2015年1月在福建平潭试验中获取的810组风速与雷达相对应的有效数据进行分组，其中539组用于训练拟合经验模型，271组用于验证风速反演结果。

图3为分别利用方程(4)和方程(5)对训练数据组进行拟合的结果，黑色叉号为10 m风速与雷达后向散射系数S的对应散点，红色实线为现有经验模型拟合线（S=226.7log(u10+0.75)+499），蓝色实线为本文提出的新经验公式拟合线（S=106tanh (0.3292u10-1.862)+668.8）。从图中可以明显看出，本文提出的新经验公式的结果更优，包括相关系数更高，均方根误差更低。这是由于在低风速下，风速对海面的粗糙度影响是有限的，这也就造成了在低风速时，海面后向散射强度S随风速增长缓慢；而在风速达到或超过15m/s时，海面后向散射强度S又会趋于饱和。

图4为利用不同经验模型对风速的反演结果，单位为m/s。蓝色圈为新经验模型反演结果，红色星为现有经验模型反演结果。其中现有研究的经验模型[8-9]反演结果的均方根误差 (Root Mean Square Error，RMSE)为2.9 m/s，平均相对误差(Mean Relative Error,MRE)为0.1；而本文提出的新经验模型反演结果的均方根误差为1.9m/s，平均相对误差为-0.06。由此可见，新经验模型的反演结果相对于现有模型有了较大程度上的改进。

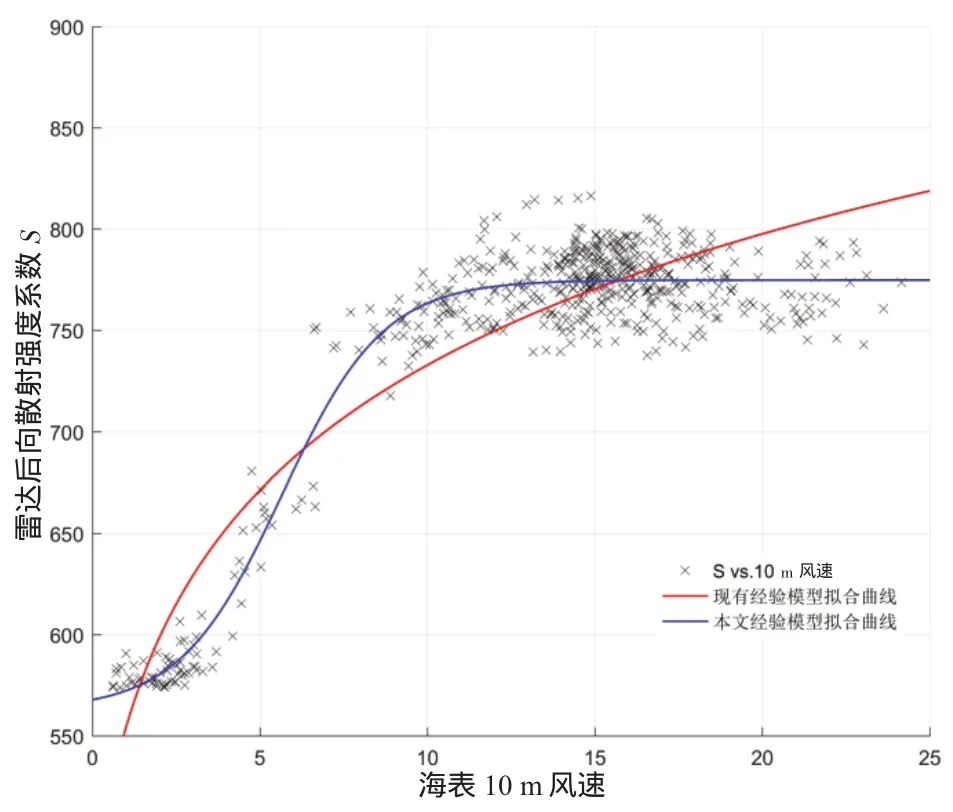
图3 10m风速与雷达后向散射系数S拟合图像

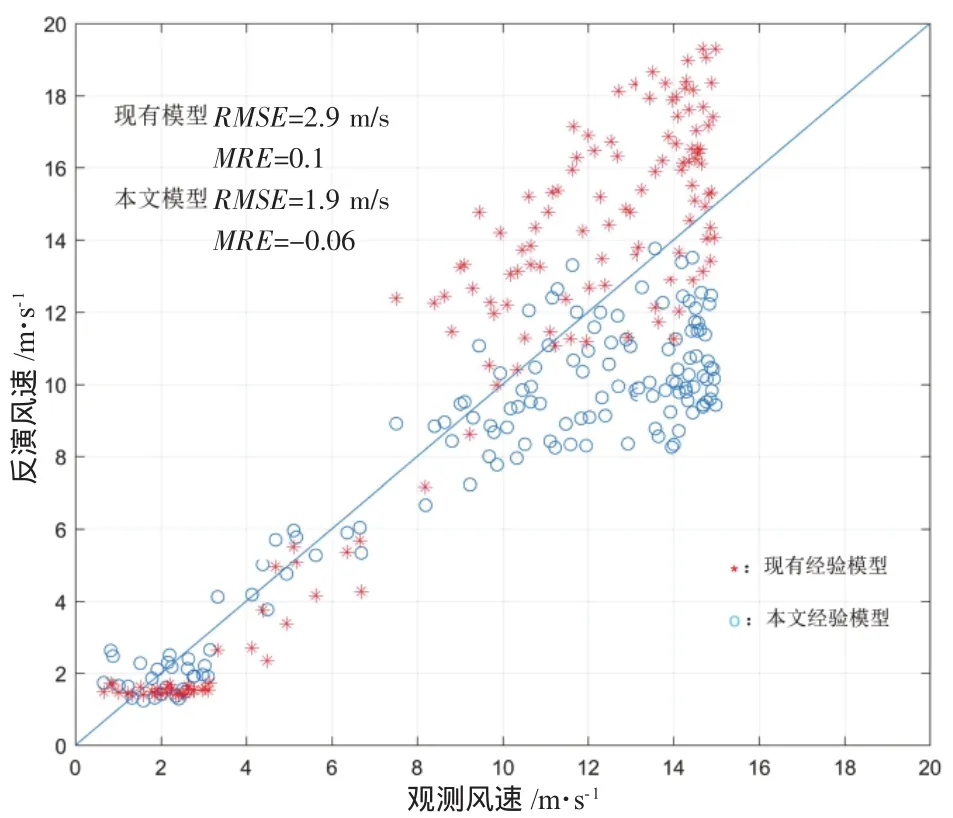
图4 雷达反演风速与实测风速对比图

2.2.2 海浪的反演结果 图5（a）和图5（b）分别为2015年1月8日5时0分在福建平潭岛试验获取的雷达图像谱和与之对应的反演获取的海浪谱。浮标测量的有效波高为2.57m，主波波向为75°，主波周期为6.7 s；风速仪测得10min平均风速为17.81 m/s，10min平均风向为84.17°。反演海浪谱计算的有效波高为1.81m，主波波向为85.38°，主波周期为5.62 s。

图5 2015年1月8日5时0分平潭岛试验获取的归一化雷达图像谱和归一化反演海浪谱

图6（a）和图6（b）分别是2015年1月15日17时0分在福建平潭岛试验获取的雷达图像谱和与之对应的反演获取的海浪谱。浮标测量的有效波高为2.06 m，主波波向为59.8°，主波周期为7 s；风速仪测量的10min平均风速为13.07m/s，10min平均风向为65.75°。反演海浪谱计算的有效波高为2.02 m，主波波向为61.3°，主波周期为5.65 s。

图6 2015年1月15日17时0分平潭岛试验获取的归一化雷达图像谱和归一化反演海浪谱

图7（a）和7（b）分别为2015年1月6日16时0分在福建平潭岛试验获取的雷达图像谱和与之对应的反演获取的海浪谱。浮标测得海浪有效波高为2.22m，主波波向77.6°，主波周期为7 s。从图7（a）中可以看出，在图像谱中，除了能量主要集中第一象限外，在第三象限仍有明显的能量波峰存在，图像谱能量分布存在多个峰值，反映出海浪并不是单一的风浪，而本文所使用的参数化海浪谱为风浪谱，导致这一类型的图像谱对于仿真海浪谱的拟合存在非常大的误差。在反演结果中有效波高仅为0.97m，主波波向为90°，主波周期为2.92 s。

图7 2015年1月6日16时0分平潭岛试验获取的归一化雷达图像谱和归一化反演海浪谱

图8～图10分别是2015年1月6日至15日在福建平潭岛试验的99组有效数据的有效波高、主波周期和主波周期的观测数据与反演数据的对比图。风浪的筛选标准为浮标测量波向与风速计测量风向偏差在20°以内，风速大于5 m/s。其中有效波高的均方根误差为0.4m，平均相对误差为0.1；主波周期的均方根误差为1.2 s，平均相对误差为-0.1；主波波向的均方根误差为9.6°，平均相对误差为0.05。

图8 2015年1月6日至15日平潭试验有效波高对比图

图9 2015年1月6日至15日平潭试验主波周期对比图

3 讨论与展望

本文提出了一种新的利用X波段海洋雷达联合反演海面风速与海浪谱的方法，该方法不需要额外的信息输入来反演海浪谱。在风速反演部分，提出的经验物理模型相较于现有模型，有效提升了风速反演的精度。在海浪反演部分，通过对比实验数据和雷达反演数据，对反演方法进行了验证，风速反演的均方根误差达到1.9m/s，有效波高的均方根误差为0.4 m，主波周期的均方根误差为1.2 s，主波波向的均方根误差为9.6°，证明了该方法的可行性。与现有研究相比，该方法还具有不需要对有效波高反演进行定标的优点。

在未来的工作中，将继续寻找有效方法提高风速反演的精度，尤其是低海况情况下风速的反演和涌浪占主体或者混合浪的海浪谱的反演。另外需要采用多地点长时间序列的观测数据对方法进行进一步验证，并提高风速和海浪谱的联合反演精度与反演效率。

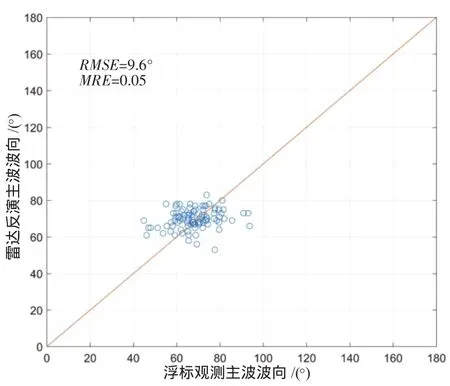
图10 2015年1月6日至15日平潭试验主波波向对比图

[1]WrightFF.WaveObservationsby Ship-Board Radar[J].Ocean SciOcean Eng,1965,1:506-514.

[2]Ziemer F,RosenthalW,Carlson H.MeasurementsofDirectionalWave Spectraby Ship Radar[C]//IAPSOSymp,General Assembly,Int Assoc Phys SciOceans,Hamburg,Germany,1983.

[3]Young I R,Rosenthal W,Ziemer F.A Three-Dimensional Analysis of Marine Radar Images for the Determination of Ocean Wave Directionality and Surface Currents[J].JournalofGeophysicalResearch Oceans,1985,90(C1):1049-1059.

[4]DankertH,RosenthalW.Ocean Surface Determination from X-Hand Radar-Image Sequences[J].Journal of Geophysical Research Oceans,2004,109(C4):1-11.

[5]王剑,段华敏.X波段雷达图像提取海洋表面风场[J].海洋技术学报,2010,29(3):5-8.

[6]Lund B,Graber H C,Romeiser R.Wind Retrieval From Shipborne Nautical X-Band Radar Data[J].IEEETransactionson Geoscience &Remote Sensing,2012,50(10):3800-3811.

[7]王慧,卢志忠.基于波数能量谱的海面风向反演算法[J].华中科技大学学报:自然科学版,2014(12):96-100.

[8]Vicenbueno R,Horstmann J,TerrilE,etal.Real-TimeOceanWind VectorRetrieval from Marine Radar Image SequencesAcquired at Grazing Angle[J].JournalofAtmospheric&Oceanic Technology,2013,30(30):127-139.

[9]HuangW,Wang Y.A Spectra-Analysis-Based Algorithm forWind Speed Estimation From X-Band NauticalRadar Images[J].IEEE Geoscience&Remote Sensing Letters,2016,13(5):701-705.

[10]Chen Z,He Y,Zhang B,etal.Determination of Nearshore Sea SurfaceWind Vector from Marine X-Band Radar Images[J].Ocean Engineering,2015,96:79-85.

[11]Hasselmann D E,Dunckel M,Ewing JA.DirectionalWave Spectra Observed During JONSWAP 1973[J].Journal of Physical Oceanography,1980,10(8):1264-1280.

[12]崔利民.X波段雷达海浪与海流遥感机理及信息提取方法研究[D].青岛：中国科学院研究生院(海洋研究所),2010.

[13]吴艳琴,吴雄斌,程丰,等.基于X波段雷达的海洋动力学参数提取算法初步研究[J].遥感学报,2007,11(06):817-825.

[14]Goda Y.Random Seasand Design ofMaritime Structures[M].World Scientific,2000:443.

[15]PlantW J.The Modulation Transfer Function:Conceptand Applications[M]//Radar Scattering from Modulated Wind Waves.Springer Netherlands,1989:155-172.

[16]Chen Z,He Y,Zhang B,etal.ANew Algorithm to RetrieveWave Parameters From Marine X-Band Radar Image Sequences[J].IEEE Transactionson Geoscience&Remote Sensing,2014,52(7):4083-4091.

[17]王淑娟.X波段雷达图像的海浪信息提取[D].青岛：中国海洋大学,2007.

[18]Zhang B,LiX,PerrieW,etal.Synergistic MeasurementsofOceanWinds and Waves from SAR[J].JournalofGeophysicalResearch Oceans,2015,120(9):6164-6184.

Research on theWind-Wave Synergistic Retrieval Method Based on X-Band Marine Radar Observations

QIU Ji-dong,ZHANG Biao,CHEN Zhong-biao,HE Yi-jun
School ofMarine Sciences,Nanjing University of Information Science and Technology,Nanjing 210044,Jiangsu Province,China

This paper presents a new method for synergistic retrieval of ocean surface wind speeds and wave spectrum based on X-band marine radar observations.The proposed algorithm needs not any external data source to obtain wave information.The surface wind speeds are first estimated based on an empirical relationship between the wind speed and radar scattering intensity.Subsequently,the ocean surface wave spectrum is retrieved byminimizing the constraint function including the simulated wave spectrum and observed radar image spectrum.The retrieved wind and wave parameters are compared with thosemeasured by anemometers and buoys. The rootmean square error(RMSE)ofwind speed,significantwave height,and dominantwave period and wave direction is 1.9m/s,0.4m,1.2 s and 9.6°,respectively.

X-band marine radar;wind speed;wave spectrum;synergistic retrieval

P714；P225.1

A

1003-2029（2017）01-0001-06

10.3969/j.issn.1003-2029.2017.01.001

2016-08-15

江苏省青年基金资助项目（BK20150905）

邱吉东（1991-），男，硕士研究生，主要研究方向为海洋微波遥感。Email:jidong.qiu@nuist.edu.cn