基于加速度反演频域动载荷的一种正则化途径*

彭凡，王樑，肖健，胡绚，韦冰峰

(1.湖南大学 机械与运载工程学院，湖南 长沙 410082; 2.北京强度与环境研究所，北京 100076)

基于加速度反演频域动载荷的一种正则化途径*

彭凡1†，王樑1，肖健2，胡绚1，韦冰峰2

(1.湖南大学 机械与运载工程学院，湖南 长沙 410082; 2.北京强度与环境研究所，北京 100076)

基于加速度频响函数矩阵反演频域动载荷是病态逆问题，反求的结果精度差，对数据的小扰动敏感，基于Tikhonov正则化方法，提出一种反演途径，将测点响应与待求激励进行归一化变换，在此基础上引入变换后的频响函数矩阵和正则化泛函进行求解，应用广义交叉验证准则选取最优正则化参数.考虑简支矩形薄板上的4个动载荷的识别问题，分析激励点和响应测点的不同位置以及动载荷大小之间相差程度不同的4个算例，将本文方法与不采用归一化变换的正则化求解结果进行2种相对误差的均方根比较.结果表明，利用归一化变换可提高动载荷反演精度，增强正则化方法的抗噪能力，当测点之间的响应以及各动载荷大小相差较大时，明显改善了识别精度.

动态载荷；频响函数；反问题；正则化；归一化

载荷识别的理论和应用研究受到了研究者越来越多的重视[1-5],目前，人们已提出了多种频域内反演动态载荷的技术，其中频响函数矩阵求逆是一类重要方法[6-7].然而，反演的病态特性使得量测数据的小扰动导致结果不准确，甚至不可信.当以测点的加速度频域响应作为输入时，低频段的反演误差非常明显.正则化方法是提高反求精度和稳健性的一条重要途径，典型的正则化方法包括截断奇异值分解和Tikhonov正则化方法[8].截断奇异值分解法的基本思想是将所得的广义解式子右端进行截断[9]，即只保留前面若干个对应于较大奇异值的部分，将后面的对应于较小奇异值的部分过滤掉，如何选取截断阈值，是该方法的难点.Tikhonov正则化方法通过引入包含响应残差和激励的模的泛函，由泛函对载荷的一阶偏导为零，得到正则化以后的激励求解列式[10-11].文献[12-13]提出综合使用奇异值分解法与Tikhonov正则化的载荷识别策略，当频响函数矩阵的条件数大于某一临界值时，使用正则化技术，反之，由奇异值分解法实施反求.张磊等[14]提出在总体最小二乘算法的基础上进行Tikhonov正则化，利用共轭梯度法解算该目标函数的最优化问题.然而，当各响应测点的响应之间、响应与激励之间以及激励与激励之间在数量上差别大，会导致正则化方法效果差，有必要重新考察变分泛函的构造.为此，文中由归一化变换使得加速度响应和激励的模值在一个相近的范围内变化，在此基础上重新构造变分泛函，给出一种Tikhonov正则化求解途径，通过简支矩形薄板的多点载荷反求算例检验其有效性.

1 问题的归一化变换及正则化求解

测点的响应向量与待求激励向量之间满足：

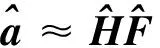
(1)

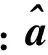
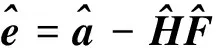
(2)

考虑n>m，由Tikhonov正则化方法, 引入残差向量模与激励向量模表示的泛函[3]:

(3)

式中:λ为正则化参数;上标“H”表示共轭转置运算.由泛函对力取极值得到:

(4)

式中:I为m阶单位矩阵.将式(1)中的频响函数矩阵进行奇异值分解:

(5)

式中:U和V为酉矩阵；S为对角奇异矩阵.令式(4)中的λ=0，然后结合式(5)，可得到载荷反求的奇异值分解方法，等价于最小二乘解[2]：

(6)

进一步考察式(2)和式(3)可见，当各响应测点的响应之间、响应与激励之间以及激励与激励之间在模值上存在较大差别时，泛函取极值并不一定能够保证各个待求激励有相近的精度，甚至可能出现正则化方法失效的情况.本文提出Tikhonov正则化方法的改进策略，将频域中的响应向量与激励向量的各分量幅值变化范围进行归一化处理，使它们具有接近相同的变化范围，令

(7)

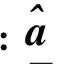
(8)

式中：qi(i=1,…,n)和ri(i=1,…,m)称为归一化因子，qi和ri可取为第i个响应与激励的模值在所考虑频段内的平均值.进一步引入变换后的频响函数矩阵：

(9)

归一化动载荷的最小二乘解为:

(10)

将式(5)代入式(9)，得

(11)

再将式(11)代入式(10),有

(12)

结合式(12)和式(7)，可见式(12)和式(6)是相同的，表明归一化变换后，载荷反求的最小二乘解与变换前是一致的.

采用Tikhonov正则化方法求解归一化变换后的反演问题,引入以下泛函：

(13)

(14)

式(14)和式(4)分别表示了经过归一化变换和未经归一化处理的正则化方法.将式(14)求得的激励代入式(7)的第二式，得到真实载荷向量.因为激励是待求量，为得到相应的归一化因子ri，可先将反求问题在所考虑的频段内进行奇异值分解求解，由此得到各激励大小的平均值，以此作为归一化因子的估计值.

确定式(4)和式(14)中正则化参数是算法的关键，文中采用广义交叉验证法(GCV)[15]确定最优正则化因子，它使下面函数取最小值.

(15)

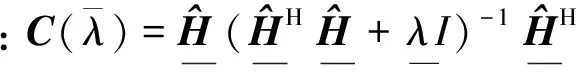
2 算例及讨论

2.1 算例设计及误差定义

考虑图1所示四边简支的矩形薄板，其尺寸为600mm×500mm×1.2mm，弹性模量为207GPa，密度为7 850kg/m3，泊松比为0.3，取模态阻尼比为0.03.矩形薄板的前3阶固有频率分别为19.8，44.1和54.8Hz.薄板受横向动载荷F1，F2，F3和F4作用，激励频率为10～300Hz.在矩形薄板上布置7个响应测点ai(i=1,…,7)，利用有限元计算获得频响函数及Fi(i=1,…,4)作用下测点的横向加速度时域响应，加入噪声，以模拟实测响应.频响函数的高斯白噪声模型为：

N(ω)=Nndej2πNud.

(16)

式中:j为虚数单位；Nud为0～1之间均匀分布随机数；Nnd为正态分布的随机数，其均值为0，方差为A(ω)10-(B/20)， A(ω)为频响函数的幅频值，B为信噪比SNR.给测点的时域响应加入噪声的模型为：

(17)

算例考虑两组激励力和响应测点的位置组合，组合Ⅰ与组合Ⅱ的坐标分别绘于图1(a)和(b)，坐标值分别列于表1与表2.在位置组合Ⅰ中，载荷F4作用点和测点4都靠近简支边界；而在组合Ⅱ中，两者都移向板中心，而F1的作用点及测点1成为最靠近边界的点.显然，载荷靠近边界，激发的振动响应减弱，不利于反求精度的提高.对每一组位置组合，分别讨论如表3所示的两种加载条件，在10～300Hz的频率段内，每个频域载荷的大小为常数.加载条件Ⅰ中的4个载荷频域值之间差别较大，有关系F1= 5F2= 10F3= 20F4；加载条件Ⅱ的4个载荷频域值相等.

对每个动态力，引入相对误差的均方根值来比较载荷识别的精度，有

(18)

式中:εi表示第i个动载荷的识别误差，为各频点的均方根值； FRi,k为第i个动载荷在第k个频率点的反求幅频值；FTi,k为实际幅频值；n为10～300Hz内的频率点数.

取各动载荷识别误差的平均，可得到总体平均误差为：

(19)

式中:nf为待识别激励数目.

相应于两组位置组合分析两组算例，为便于结果对比，统一取频响函数的信噪比SNR=30dB.加速度响应的2种噪声水平分别为η=5%和10%.

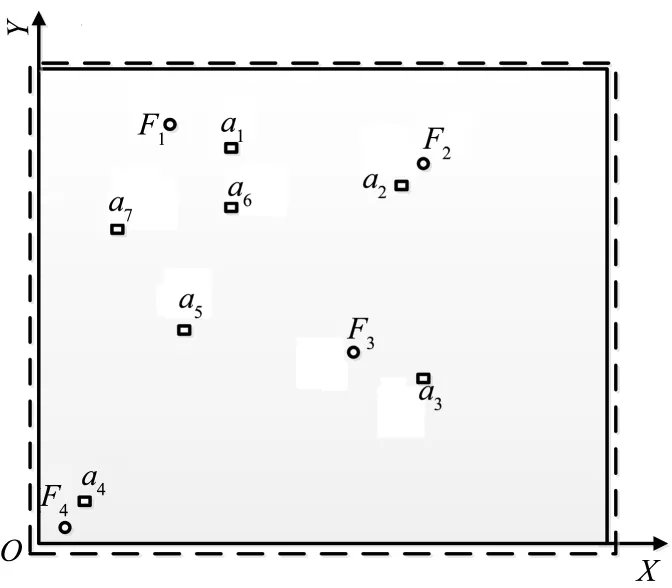
(a)位置组合Ⅰ

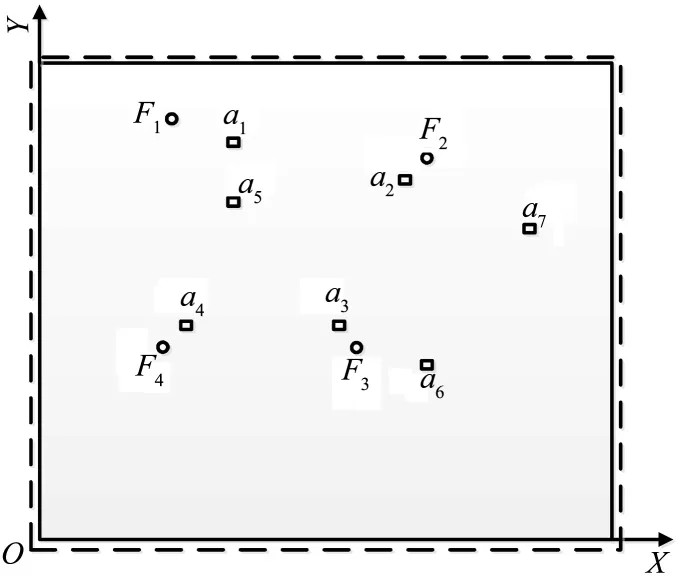
(b)位置组合Ⅱ

表1 位置组合Ⅰ的坐标

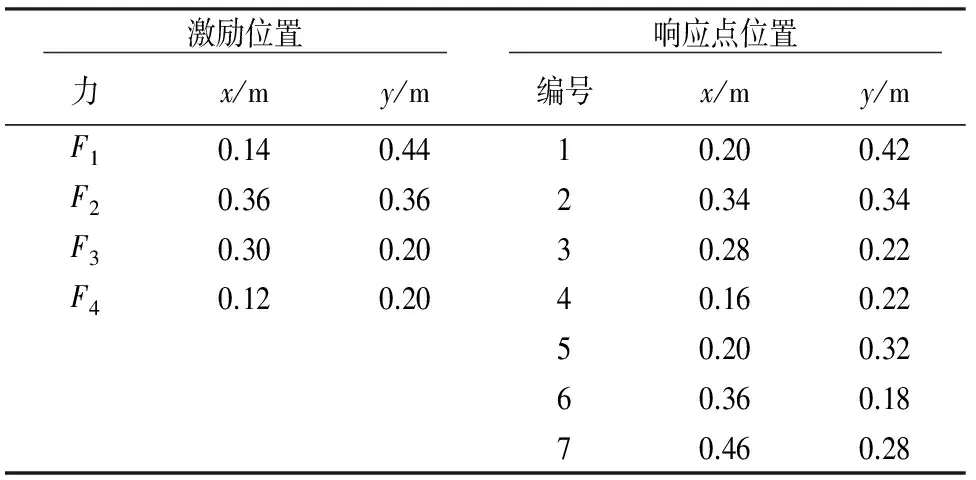
表2 位置组合Ⅱ的坐标

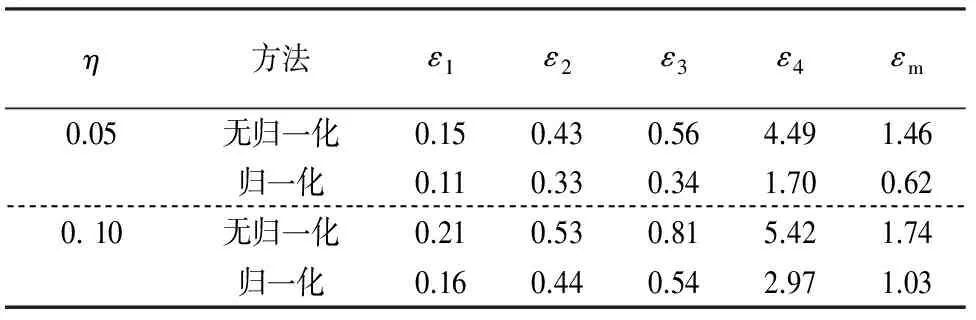
表3 对应位置组合Ⅰ和载荷条件Ⅰ的相对误差

2.2 算例1

对于表1所示位置组合Ⅰ的动载荷，考虑加载条件Ⅰ，分别采用不经归一化处理和经过归一化处理的正则化方法反求载荷，结果如图2所示.由图2可知， 4个反演载荷均在低频范围内波动大，在较高频段内，反求值与实际值相差很小.这是因为基于加速度反求的逆运算项之模值随频率减小而显著增加，随频率增加而减小，故在低频段，频响函数矩阵求逆的条件数较大，导致较大的误差与波动.图2表明，归一化变换后的正则化求解能提高识别精度，尤其在低频段内，效果明显.而在大于二阶基频(约45 Hz)的频率段，两种反演途径给出的结果接近相同.

由2种正则化途径所得载荷的相对误差结果如表3所示.由表3可知，F4的识别误差最大，这是因为F4的频域值最小，且最靠近边界.经过归一化变换后，各载荷的相对误差都减小了，尤以F4的降低最明显，总体平均误差也下降较多.

f/Hz

f/Hz

f/Hz

f/Hz

分析载荷频域值相同的加载条件Ⅱ，识别误差结果如表4所示.由表4可知，2种正则化途径所得结果的误差相比表3列出的对应值减小，归一化处理对F1，F2和F3的识别效果改善较小，但明显提高了F4的识别精度.这是因为F4接近边界，产生的测点加速度响应小，归一化变换将其影响放大了，使得其识别精度得到提高.

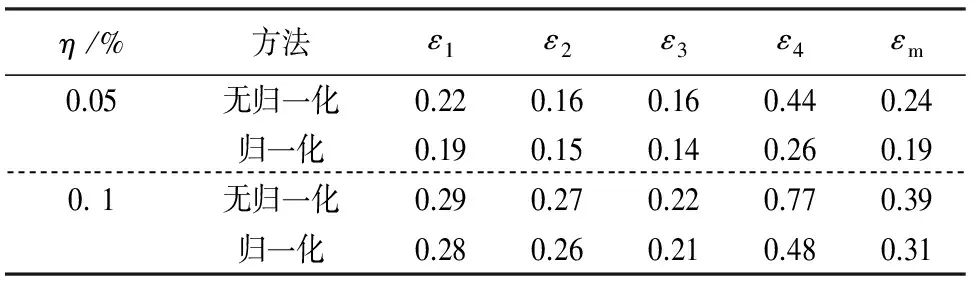
表4 对应位置组合Ⅰ和载荷条件Ⅱ的相对误差

2.3 算例2

分析位置组合Ⅱ，首先考虑载荷条件Ⅰ，误差结果如表5所示.比较表5与表3可见，F4的误差减小，而F1的误差有所增加，主要原因是此位置组合中的F4作用点靠近板中部，从而激发了较强的响应，而F1相对其余3个载荷更靠近边界.归一化变换改善了反求的总体精度，且明显降低了F4的相对误差.

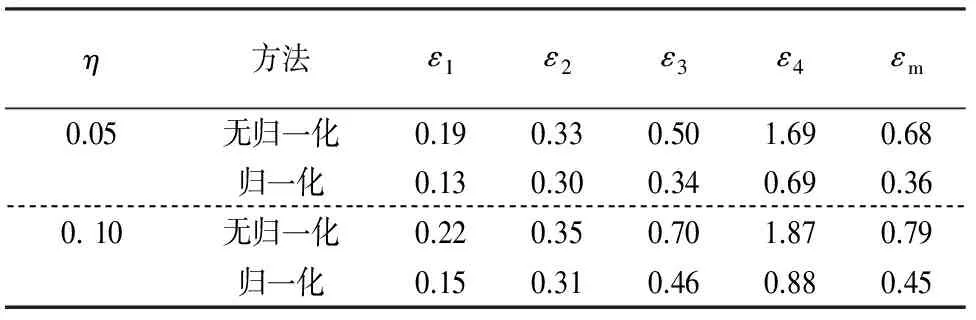
表5 对应位置组合Ⅱ和载荷条件Ⅰ的相对误差

考虑载荷条件Ⅱ，误差如表6所示.从总体和个体来看，2种正则化途径所给结果的识别精度接近相同，原因在于4个频域载荷相同，且作用点离边界较远以及各测点频域相应的强度接近相同.同样由于F1离边界相对最近，故识别误差最大的载荷由F4变成了F1，而归一化处理使得F1的识别误差略有减小.

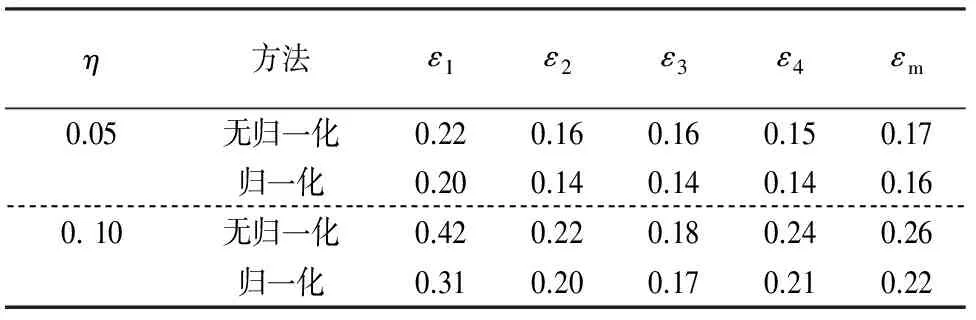
表6 对应位置组合Ⅱ和载荷条件Ⅱ的相对误差

3 结 论

在频域中采用归一化变换，将各测点响应和待求载荷的大小变化调整到相近的范围，构造新的Tikhonov泛函进行正则化求解.利用数值仿真所得结果可知：

1)归一化处理能从整体和个体上提高各动载荷的反演精度.

2)当频域动载荷大小相差较明显，或者载荷作用点靠近边界时，归一化处理使得相应荷载的反求精度明显改善，抵抗测量噪性干扰的能力增强.

[1] LNOUE H,HARRIGAN J J,REID S R. Review of inverse analysis for indirect measurement of impact force[J].Applied Mechanics Review,2001,54(6):503-525.

[2] 韩旭,刘杰,李伟杰,等.时域内多源动态载荷的一种计算反求技术[J].力学学报,2009,41(4):595-602.

HAN Xu, LIU Jie, LI Weijie,etal.A computational inverse technique for reconstruction of multisource loads in time domain[J].Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(4):595-602.(In Chinese)

[3] SU N, LIU J ，HAN X,etal. A new improved regularization method for dynamic load identification[J].Inverse Problem in Science and Engineering,2014,22(7):1062-1076.

[4] 彭凡,马庆镇，肖健，等.整体平动自由结构载荷时域识别技术研究[J]. 振动与冲击，2016，35(6):95-99.

PENG Fan, MA Qingzhen, XIAO Jian,etal. Research on load identification in time domain for free structures with oval translation[J].Journal of Vibration and Shock,2016,35(6):95-99.(In Chinese)

[5] 彭凡，王樑，肖健.质量时变系统的动载荷识别[J].湖南大学学报:自然科学版，2016,43(8):52-56.

PENG Fan, WANG Liang, XIAO Jian. Identification of dynamic loads in mass-variable system[J]. Journal of Hunan University：Natural Sciences, 2016, 43(8):52-56.(In Chinese)

[6] SANCHEZ J, BENAROYA H.Review of force reconstruction techniques[J]. Journal of Sound and Vibration,2014, 333(14): 2999 -3018.

[7] 刘恒春，朱德懋，孙久厚.振动载荷识别的奇异值分解法[J].振动工程学报,1990,3(1)：24-33.

LIU Hengchun, ZHU Demao,SUN Jiuhou.A singular value decomposition method for the identification vibration loads[J]. Journal of Vibration Engineering,1990,3(1):24-33.(In Chinese)

[8] NELSON P A,YOON S H. Estimation of acoustic source strength by inverse of methods: partⅠ,conditioning of the inverse problem[J]. Journal of Sound and Vibration, 2000, 233(4):643-668.

[9] THITE A N，THOMPSON D J.The quantification of structure structure borne transmission paths by inverse methods. part1: improved singular value rejection methods[J]. Journal of Sound and Vibration, 2003,264(2/3): 411-431.

[10]KIM Y, NELSON P A. Optimal regularisation for acoustic source reconstruction by inverse methods[J]. Journal of Sound and Vibration，2004, 275(3/5):463-487.

[11]CHOI H G,THITE A N,THOMPSON D J. Comparison of methods for parameter selection in Tikhonov regularization with application to inverse force determination [J]. Journal of Sound and Vibration, 2007,304(3/5):894-917.

[12]CHOI H G, THITE A N, THOMPSON D J. A threshold for the use of Tikhonov regularization in inverse force determination[J]. Applied Acoustics, 2006,67(8):700-719.

[13]郭荣，房怀庆，裘剡,等.基于Tikhonov正则化及奇异值分解的载荷识别方法[J].振动与冲击，2014,33(6)：53-58.

GUO Rong, FANG Huaiqing,QIU Shan,etal. Novel load identification method based on the combination of Tikhonov regularization and singular value decomposition[J].Journal of Vibration and Shock,2014, 33(6):53-58 .(In Chinese)

[14]张磊，曹跃云，杨自春，等.总体最小二乘正则化算法的载荷识别[J]. 振动与冲击, 2014，33(9):159-164.

ZHANG Lei, CAO Yueyun, YANG Zichun,etal.Load identification using CG-TLS regulariztion algorithm[J]. Journal of Vibration and Shock,2014,33(9):159-164.(In Chinese)

[15]GOLUB G H, HEATH M, WAHBA G. Generalized Cross-Validation as a method for choosing a good ridge parameter [J]. Technometrics, 1979,21(2): 215-223.

A Regularization Approach of Dynamic Load Identification in Frequency Domain by Acceleration Responses

PENG Fan1†,WANG Liang1，XIAO Jian2，HU Xuan1, WEI Bingfeng2

( 1. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China; 2. Research Institute of Beijing Structure and Environment Engineering，Beijing 100076, China)

Load identification based on acceleration frequency response matrix is an ill-conditioned problem. The identification accuracy can obviously be affected by small perturbations of the response data. Based on Tikhonov regularization method, a new approach is proposed in which both the response data at measured points and the loads to be identified are normalized, the transformed frequency response matrix and regularization function are introduced, and the corresponding problem of functional minimum is solved to obtain the loads. The optimal regularization parameters are determined by generalized cross validation criterion. The identification of four transverse dynamic loads on a rectangular thin plate with simply supported edges is performed. Four numerical examples are designed to have different application locations of loads and measured points as well as different magnitude ratio of dynamic loads in frequency domain. The results show that the new approach of dynamic load identification in frequency domain is effective to improve the identification accuracy and the noise resistance. Particularly, the errors of the identification can be significantly reduced in the cases where the large difference between the magnitudes of dynamic loads in frequency domain exists, or when excitation positions are close to structural boundaries.

dynamic loads; frequency response function; inverse problem; regularization; normalization

1674-2974(2017)02-0075-05

10.16339/j.cnki.hdxbzkb.2017.02.011

2016-02-20

湖南省自然科学基金资助项目(11JJ3001), Natural Science Foundation of Hunan Province of China(11JJ3001)

彭凡(1963-)，男，湖南湘乡人，湖南大学教授，博士

†通讯联系人，E-mail:fanpeng@hnu.edu.cn

O326；O347.1

A