不确定需求下集装箱支线物流网络鲁棒优化

杨虎祥，赵学彧，刘炳城，冯 琪

（武汉理工大学 交通学院，湖北 武汉 430063）

不确定需求下集装箱支线物流网络鲁棒优化

杨虎祥，赵学彧，刘炳城，冯 琪

（武汉理工大学 交通学院，湖北 武汉 430063）

集装箱支线物流网络规划设计其实质是带时间窗约束的车辆路径优化问题在船舶领域的另一种应用。枢纽港或中心货源地及各支线港货运需求会随着区域经济形势的起伏与航运市场波动而变动，因此在优化支线物流网络时须考虑货运需求的不确定性。在现有已知货运需求研究的基础上利用鲁棒优化方法对原有的模型及算法进行改进，使其既能够满足系统对优化效果和稳定性的要求，同时有效的弥补了现有的确定需求情况下支线物流网络的不足，增强物流企业的抗风险能力。

时间窗；支线物流网络；鲁棒优化；不确定需求；集装箱

1 引言

在新的经济形势和营运条件影响下，物流公司为了追求自身效益和运营管理的经济性，减少大型集装船舶在主干线上的挂靠港口数量，提高大型集装箱船舶的满载率且缩短船舶的滞港时间，以大型港口为中心辐射中小型港口的网状结构已成为航线结构的新常态。有关区域支线运输的研究也越来越被重视并逐步与干线运输分离，国际航线结构正在完成由线状向网状的转化[1]。轴辐式网络有效改善了频繁挂靠的局限性，以枢纽港为中心货源地根据运输需求逐步向区域内的中小港口辐射，建立高速发达的集装箱物流支线网络已成为各航运公司发展的核心战略。但是近几年区域支线运输市场竞争过度，部分航运企业为了保证市场份额，一味的打价格战甚至不惜亏本，普遍效益不佳[2]。究其原因主要有两个方面：一方面各支线港功能定位不准，主管单位对区域支线物流网络节点缺乏统一的规划及布局；另一方面集装箱运输的货源在空间和时间上分布的不均衡性和货物本身对时效性的要求，支线物流网络运输决策需要考虑的因素众多，与干线物流网络的构建相比更为复杂。

2 集装箱支线物流网络的研究综述

现有的理论研究成果中利用分层规划的思想，主要分为枢纽港的选址、区域支线港确定、航线设计、船舶调度、航线船型的匹配。大多数研究只涉及一个问题的决策，只有较少的研究将其中两个问题相结合进行研究，如航线设计及航线船型匹配、航线设计与枢纽港的选定等问题[3]。区域中心货源地的选择一般采用模糊聚类分析法、主成分分析法等定性方法进行研究[4]。大多数航线设计问题的研究对象都是基于选定的中心货源地，以总成本最低、集装箱船舶总航行时间最短为目标，根据实际情况设定约束条件构建混合规划模型，从而构建区域集装箱支线物流网络[5]。考虑到整个航运市场的起伏波动会影响各支线之间及各支线港与枢纽港货运量随之变化：对航线进行动态优化，面对不确定的集装箱需求量，采用固定间隔取样，综合判断现行航线是否满足货运需求的变化，若不能及时变更或重新设计新航线；或是引入不确定理论研究在变动的货运需求情况下集装箱支线物流网络优化模型[6]。目前关于集装箱支线物流网络的研究主要集中于优化模型和求解算法，根据实际情况，结合车辆调度问题建立混合整数规划模型或非线性规划模型并求解，实现航线设计与船舶的调度[7]。

通过总结以上集装箱支线物流网络优化方法研究现状可知，集装箱支线物流网络的研究较多，但确定性货运需求研究居多。本文考虑航运市场的波动，运用鲁棒优化方法能够满足系统对优化效果和稳定性的要求，在设计优化集装箱支线物流网络时应用鲁棒优化建立支线物流网络鲁棒优化模型，有效弥补了现有确定性需求研究的不足，减缓由于货运需求波动而带来的不利影响，增强航运企业的抗风险能力[8]。

3 集装箱运输支线物流网络鲁棒优化模型的建立

3.1 需求不确定下的集装箱运输支线物流网络优化问题描述

集装箱支线物流网络优化实际上是多程多车辆路径优化问题[9]，本文的研究内容是由某一特定枢纽港（本文指中心货源地）向多个支线港进行集装箱集疏运，与VRP存在一定的相似性。从具体研究内容来看，本文所研究的支线网络是轴辐式网络优化中支线物流网络优化层面，考虑到实际情况中的不确定因素，本文选择松弛的时间窗，假设提前到达接货点（支线港）的情况下无在港等待成本，并引入惩罚成本PC（不满足软时间窗的情况加以惩罚）。本文研究集装箱航运公司如何规划船队中船舶由枢纽港向支线港提供服务的航线，在满足客户需求的前提下使得总成本(运输成本与惩罚成本)最小，即图1中虚线方框内由枢纽港1向支线港1，2，3，4，5，6运送集装箱的问题。

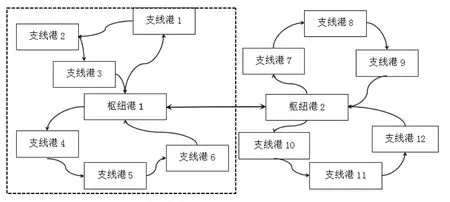
图1 目标支线网络优化问题示意图

支线港之间及支线港与枢纽港之间的货运需求量是网络设计的重要依据，现有的理论研究多偏向于确定性支线物流网络优化问题。实际上集装箱支线物流网络的设计易受到货运需求的波动性影响，集装箱物流运输公司在做规划时很难明确规划期内的运输需求，也就是说运输需求是一个不确定的参数，因此本文在规划、优化航线时将不确定性加以考虑。本文以总成本最优为目标建模，基于不确定性需求研究支线物流网络优化问题，利用鲁棒优化思想，对集装箱运输支线航线进行优化，同时选取不同的情景集来描述涉及到的不确定性问题。

3.2 模型的假设、符号说明

（1）模型假设。本文研究的是需求不确定下的集装箱支线物流网络优化问题，考虑到实际情况与求解的难易程度，做出以下假设。

①物流运输船队由不同载箱量的集装箱船舶组成且每种船型的运营参数可以查到。

②任意支线港口的到达时间由其上一港口的到达时间决定，忽略在港的等待时间和服务时间且每个卸货港仅由一艘船舶提供一次服务。

③为简化问题本文不考虑空箱调配，不考虑枢纽港容量限制及各航道通过能力。

④支线港的货运需求是由其所服务客户的库存决定的，客户接收货物通常有个给定的时间范围，所以卸货港有时间窗约束。

⑤整个航次的总成本只考虑燃油成本和装卸成本，且各支线港及枢纽港单箱装卸成本相同，早于最早服务时间到达在港等待成本不计。

（2）符号说明

集合表示：

K:表示物流运输船队所有船舶集合；

A:表示区域中所有航段集合；

参数表示：

PC:表示集装箱船舶不符合时间窗约束而产生的惩罚成本；

Qk:表示K型集装箱船的最大装载量；

di:表示i港的货运需求；

决策变量表示：

3.3 需求不确定下集装箱支线物流网络优化模型的建立

本文在现有已知货运需求研究的基础上利用鲁棒优化方法对原有的模型及算法进行改进，故先介绍确定性集装箱支线物流网络优化的相关模型。

根据相关文献，确定性需求的支线网络优化模型可表示为：

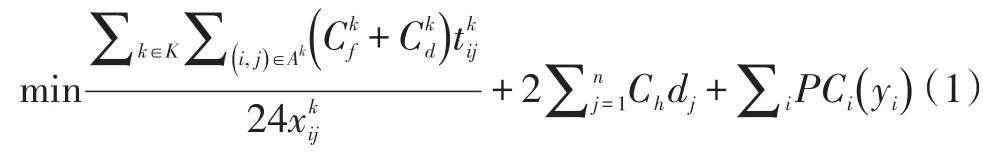
约束条件：

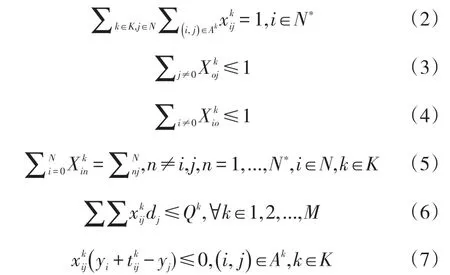
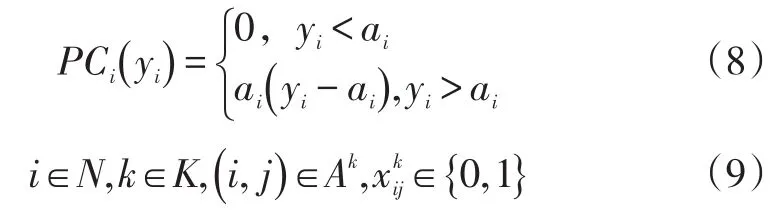
目标函数(1)表示总成本最小或最优；约束(2)确保每个支线港口只能接受一艘集装箱船一次服务且每个港口都,得到服务；约束(3)与(4)保证提供服务的集装箱船从中心货源地出发，服务完所有客户后回到中心货源地；约束(5)确保集装箱船舶必须由b港驶出，保证流量守恒；约束条件(6)用于确保船舶实际集装箱量小于等于其最大载箱量；(7)要求船舶在两港之间航行时必须保持航行连续性；(8)用于计算不符合时间窗约束情况下达到物流运输公司所要承担的惩罚成本。

为了更好地减轻不确定性给决策带来的不利影响，现将鲁棒思想应用到集装箱支线物流网络设计问题中。假设存在S个需求情景，且每种情景发生相对应的概率为PS，引入不确定性变量d，表示货运需求的不确定性，情景S下j港对应箱量为

根据相关文献，基于情景集的鲁棒优化模型可表示为：

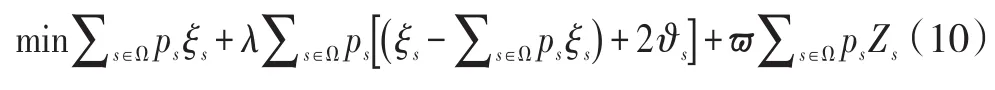
约束条件：

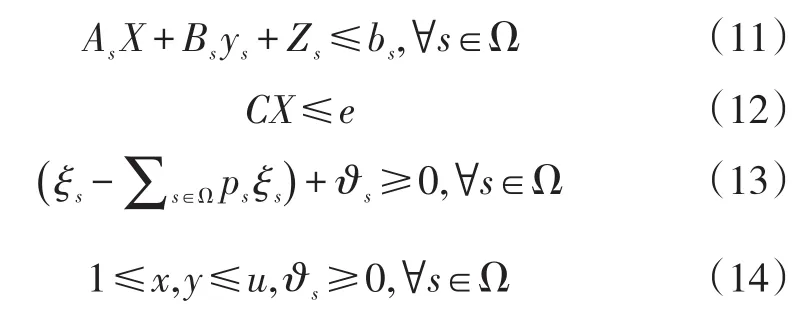
情景S对应的确定性集装箱支线物流网络鲁棒优化模型的目标函数可表示为：

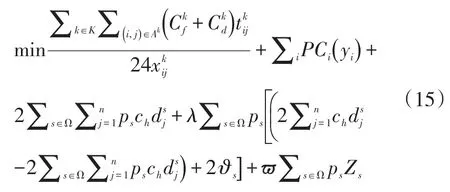
约束条件在确定性网络的基础上，新增鲁棒性约束，或对部分原约束进行鲁棒化处理，如下所示：

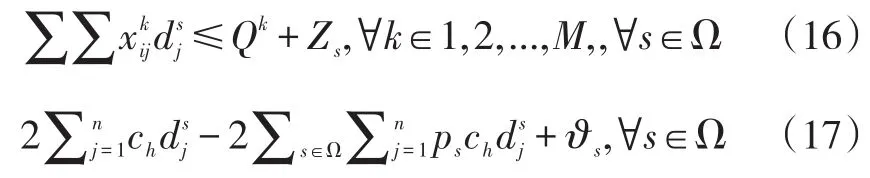
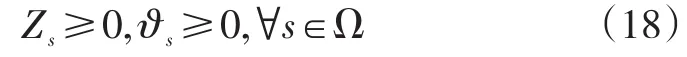
目标函数(15)由每种情景对应的目标函数(1)代入基于情景集的鲁棒优化模型目标函数(10)中得到。该鲁棒模型中不确定运输需求的所有取值都包含在情景集之中。约束条件(16),松弛了确定性模型中的船舶载箱量约束，允许运输需求与船舶最大载箱量之间存在偏差值ZS,如果船舶航次实际载箱量小于或等于其最大载箱量，则否则存在运输需求Zs无法得到运输，这部分得不到符合的货运需求通过目标函数的最后一项进行惩罚。

4 算例分析

假设B集装箱物流公司开展国际集装箱业务，在某一特定区域内构建集装箱支线物流网络。B公司在此区域共有一个枢纽港和四个支线港，船舶航行于枢纽港1与各支线港N*={2,3,4,5}之间，各港口间航程见表1。假定该支线网络有三种船型可供选择，参数见表2。各支线港运输需求及时间窗约束见表3。

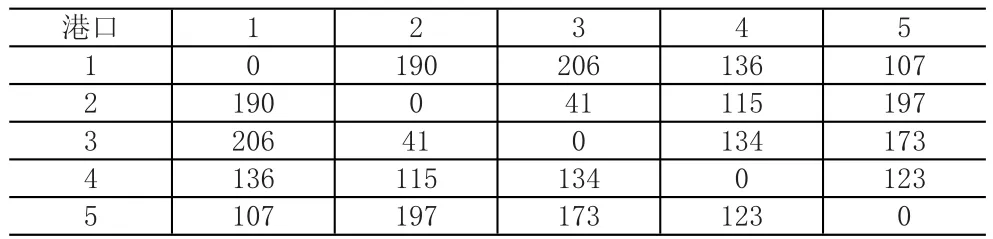
表1 各港口间航行距离（单位:nmi）

表2 部分船舶参数

表3 支线港的需求时间窗和货物需求

船舶在各港间的航行时间=港口间里程/船型对应航速；燃油成本=(航行期间日耗重油量*重油价格+航行期间日耗轻油量*轻油价格)*航行时间/24；航次成本=装卸成本+燃油成本。

设单位轻油价格5 400元/t，重油价格3 200元/t。集装箱在港装卸成本可根据单箱装卸成本进行计算，为确定装卸成本，本文以Z港为标准，假设区域中5港的单位装卸成本都与Z港持平。故本文以2015年Z港宝满港区167元/TEU的单箱装卸成本为标准，且各港单位时间惩罚成本分别设置为1 000元，2 000元，1 000元和2 000元。

由航程与各船型航速计算所得船型1、船型2和船型3在各航段航行时间与各航段航行所引致的燃油成本见表4-表6。

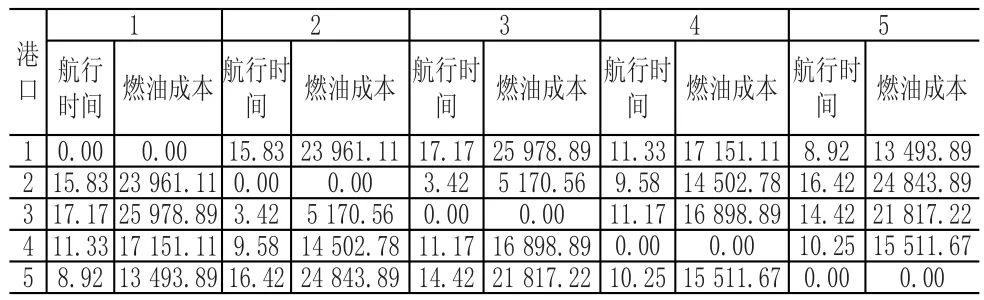
表4 船型1在各航段航行时间与各航段航行所引致的燃油成本

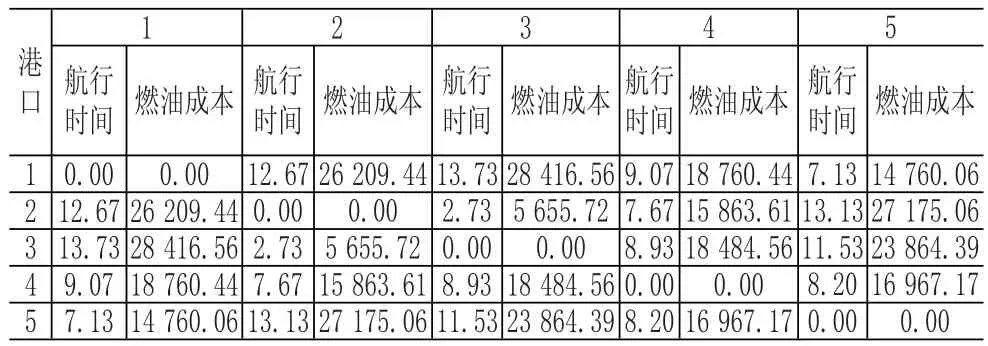
表5 船型2在各航段航行时间与各航段航行所引致的燃油成本

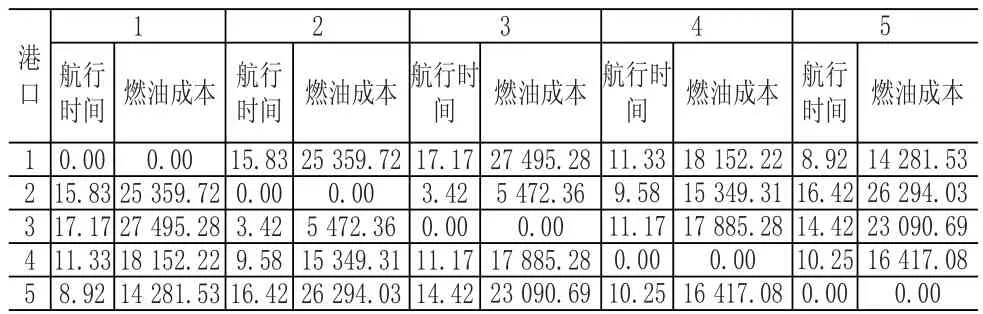
表6 船型3在各航段航行时间与各航段航行所引致的燃油成本

此外，本文假设B公司在规划期内共存在三种可能的需求情景，发生的概率分别为0.2,0.3和0.5，各情景下区域内各支线港的集装箱运输需求量见表7。另设定鲁棒参数λ为1，ϖ为100。

表7 各情景下区域内各支线港的集装箱运输需求量

运用软件Lingo对鲁棒优化模型进行求解。其模型的求解状态见表8，当参数λ为1，ϖ为100时，得到全局最优解291 389.0元，各船型船舶的最优挂靠情况为:船型1挂靠1-4-1，船型2挂靠1-3-2-1，船型3挂靠1-5-1。

比较给定需求下求解结果与鲁棒模型求解结果，前者的最优值为274 235.0元;后者的最优值291 389元，确定性模型要比鲁棒优化模型优。在运输需求确定的情况下，确定性模型得到的解是最优的，但是到运输需求发生波动时确定性模型所得到的解有可能是不可行解。鲁棒优化模型优化的航线具有一定的抗干扰能力，航线设计方案在需求发生波动时仍能保持稳定，为达到上述目的，物流公司需要以高成本为代价。

为了更直观的反映鲁棒模型所得方案的优势和模型的鲁棒性，本文将三个情景分别代入确定性模型，计算不同运输需求所对应的最优值，并将所得到的结果与鲁棒优化模型的优化结果进行对比，结果见表9。

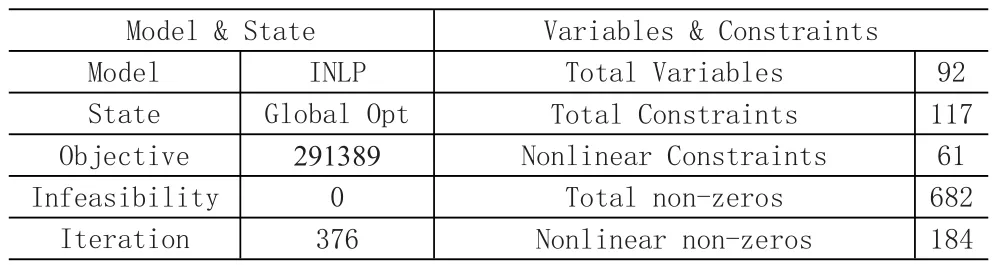
表8 模型的求解状态

表9 不同情景下运输需求量的对比

表10 不同优化方案的对比表

由表9和表10可以看出，不同需求下的集装箱船舶的最优停靠方案也不同，虽然在某一给定的需求下得到的最优解是“最优航线方案”，但是当需求变化时“最佳航线方案”可能不再最优，也有可能变为不可行解。鲁棒模型所得到的最优解是在综合考虑各种情景的前提下得到的，能够较好的降低由于需求不确定性给物流公司带来的网络设计优化决策风险。

5 结论

支线港口多为规模小的区域性港口，运输需求易受到季节等不确定因素的影响，故考虑不确定性运输需求是提高支线网络设计的科学性和可靠性的关键。本文选用鲁棒优化方法来优化集装箱支线物流网络，在研究带时间窗的车辆路径问题基础上构建集装箱支线物流网络鲁棒优化模型，同时考虑时间约束和运输需求的不确定性对支线网络设计的影响。该优化模型在满足支线港运输需求浮动的前提下缩减成本，增强了集装箱物流公司的抗风险能力，提高了公司整体竞争力。

[1]刘鲁凤.区域集装箱航运支线网络优化研究[D].大连:大连海事大学,2015.

[2]郑士源,王浣尘.支线运输市场过度竞争现象的分析及对策[J].系统管理学报,2009,(5).

[3]张蕾.集装箱支线运输班轮航线规划与配船问题研究[D].大连:大连海事大学,2011.

[4]陈芳.东南亚集装箱班轮运输支线网络构建研究[D].大连:大连海事大学,2011.

[5]焦宁泊.沿海支线集装箱运输网络优化研究[D].大连:大连海事大学,2008.

[6]计明军,陈哲,王清斌.集装箱船舶支线运输航线优化算法[J].交通运输工程学报,2011,(4):68-75.

[7]张辉.面向辽宁沿海经济带黄海翼的外贸运输物流网络优化研究[D].大连:大连理工大学,2010.

[8]伍方凌.集装箱班轮支线网络鲁棒优化模型研究[D].大连:大连海事大学,2015.

[9]Fagerholt K.Designing optimal routes in a liner shipping problem[J].Maritime Policy& Management,2004,31(4):259-268.

Robust Optimization of Container Feeder Logistics Network with Uncertain Demand

Yang Huxiang,Zhao Xueyu,Liu Bingcheng,Feng Qi
(School of Communication,Wuhan University of Technology,Wuhan 430063,China)

The planning and design of the container feeder logistics network is,in nature,an instance of the VRPTW in the vessel field. Since the freight transport demand of the pivot port or the central sourcing destination as well as the feeder ports would fluctuate with the regional economy and the shipping market,when optimizing the feeder logistics network,we must consider the uncertainty of the freight transport demand.In this paper,on the basis of previous studies on freight transport demand,we applied the robust optimization process to improve the available models and algorithms to render them compliant with the requirement for optimization performance and stability and at the same time make up for the inadequacy of the current feeder logistics network with deterministic demand.

time window;feeder logistics network;robustoptimization;uncertain demand;container

O224;U169.6

A

1005-152X(2017)02-0090-05

10.3969/j.issn.1005-152X.2017.02.022

2017-01-08

杨虎祥（1989-），男，陕西宝鸡人，硕士研究生，研究方向：现代港航与综合物流。