基于平台翻滚工况下安全带约束系统优化设计

莫易敏，沈 鹏，刘昌业,2，梁永彬，饶思敏，严 燕

(1.武汉理工大学 机电工程学院，湖北 武汉 430070；2.上汽通用五菱汽车股份有限公司，广西 柳州 540057)

汽车安全已成为制约交通运输及汽车行业发展的重要因素，对汽车安全性能研究是十分必要的。目前，国内外针对汽车正碰和侧碰事故的研究已相对成熟，并且我国的C-NCAP(China-New Car Assessment Program)法规对乘员保护及行人保护中的各项指标评分都有明确的规定。然而，针对车辆翻滚碰撞安全性方面，各国目前尚无强制性法规，仅FMVSS 208法规中涉及到整车翻滚碰撞性能检测试验,试验方法来源于SAE J2114的平台翻滚试验[1]。在FMVSS208法规中，仅规定“假人身体任何部位不允许抛出车外”一项评判指标，缺乏量化的评价指标。汽车安全带约束系统作为乘员有效的防护装置能够在事故发生时有效减少对乘员造成的损伤。翻滚事故相较于其他交通事故具有更高的死亡率，因此对翻滚工况下安全带约束系统的约束效能进行研究和优化具有十分重要的意义。

1 仿真与实验对标

1.1 多刚体模型建立

在荷兰TNO公司开发的碰撞受害者模拟软件MADYMO软件中[2]，将已有的整车有限元模型中车身关键部件的单元和节点信息导入并建立整车多刚体仿真模型。该仿真模型包括车身外部结构模型、车内环境模型、Hybrid III男性第50百分位椭球假人模型、三点式混合安全带约束系统模型以及各关键部位铰链特性、接触特性的定义等。对多刚体模型依据SAE J2114标准建立平台翻滚试验工况，建模后透明化部分表面，带假人的整车多刚体模型如图1所示。

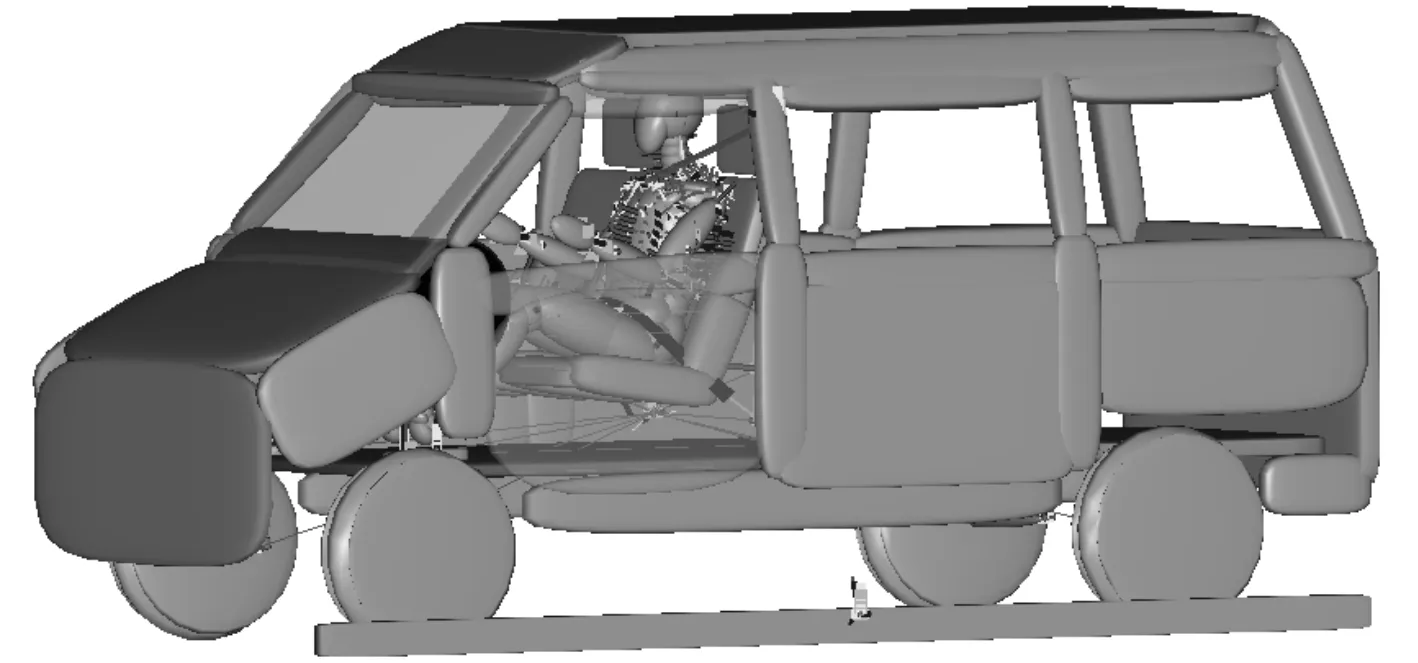
图1 带假人的整车多刚体模型

图2 假人及约束系统示意图

三点式混合安全带模型主要由卷收器、带扣、锚点、有限元安全带、多刚体安全带、限力器及预紧器组成，根据车内环境实际情况确定各个约束系统关键位置。全带模型分为多体安全带和有限元安全带。有限元安全带能够更加准确真实地模拟安全带与假人身体的接触，因此使用有限元安全带进行假人约束，与假人无接触的部分则采用多体安全带[3]。假人及安全带约束系统如图2所示。安全带限力器及预紧器均安装于卷收器位置，笔者采用MADYMO软件中的JOINT.TRAN命令定义一个滑移铰来代替安全带卷收器功能。并分别用BELT_LOAD_LIMITER、BELT_PRETENSIONER、PAYIN_TIME、BELT_RETRACTOR命令定义限力器、预紧器及织带爪卷收器的特性。限力器限力等级为4 000 N，安全带对驾驶员的约束力达到4 000 N时，限力器动作，从卷收器中放出一段安全带缓冲驾驶员胸部的压力。

1.2 仿真与试验对标

由于平台翻滚对假人的损伤比较严重，未经过优化的实车在试验过程中极有可能导致假人损坏，因此实车试验中未安置假人。因此笔者仅通过对比车辆翻滚姿态以及加速度曲线进行对标分析。首先，试验与仿真均翻滚一周，通过对比翻滚过程中关键时刻翻滚状态进行分析[4-6]，然后，分析实车试验Y向加速度曲线和仿真模型加速度曲线之间的误差，验证仿真模型的准确度与可靠性。

1.2.1 车辆翻滚状态对标

在试验与仿真中，车辆均翻滚一周。图3为仿真与试验关键运动状态对比图，表1为关键时刻的仿真结果与试验结果。

图3 仿真与试验关键运动状态对比图

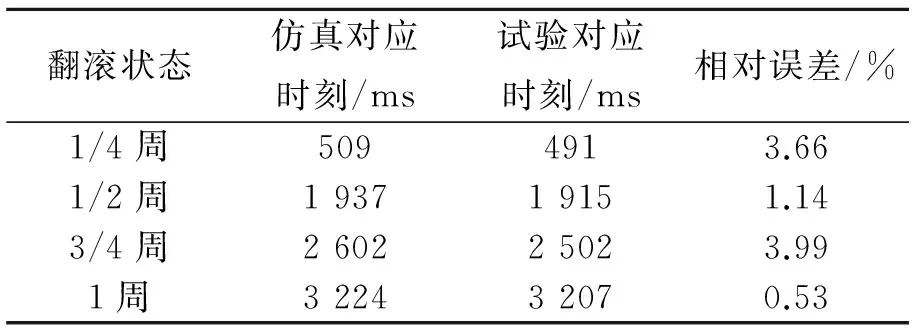
翻滚状态仿真对应时刻/ms试验对应时刻/ms相对误差/%1/4周5094913.661/2周193719151.143/4周260225023.991周322432070.53

由图3和表1可知，车辆平台翻滚过程中仿真与试验关键翻滚状态对应时刻误差均在5%以内，仿真精度较高。

1.2.2 加速度曲线对比

整车翻滚试验中，车身B柱下端变形量较小，因此在车身B柱下端安装加速度传感器来测量整车翻过过程中车辆Y向的加速度。仿真的加速度曲线与试验曲线，如图4所示。试验与仿真曲线的趋势和峰值基本吻合。

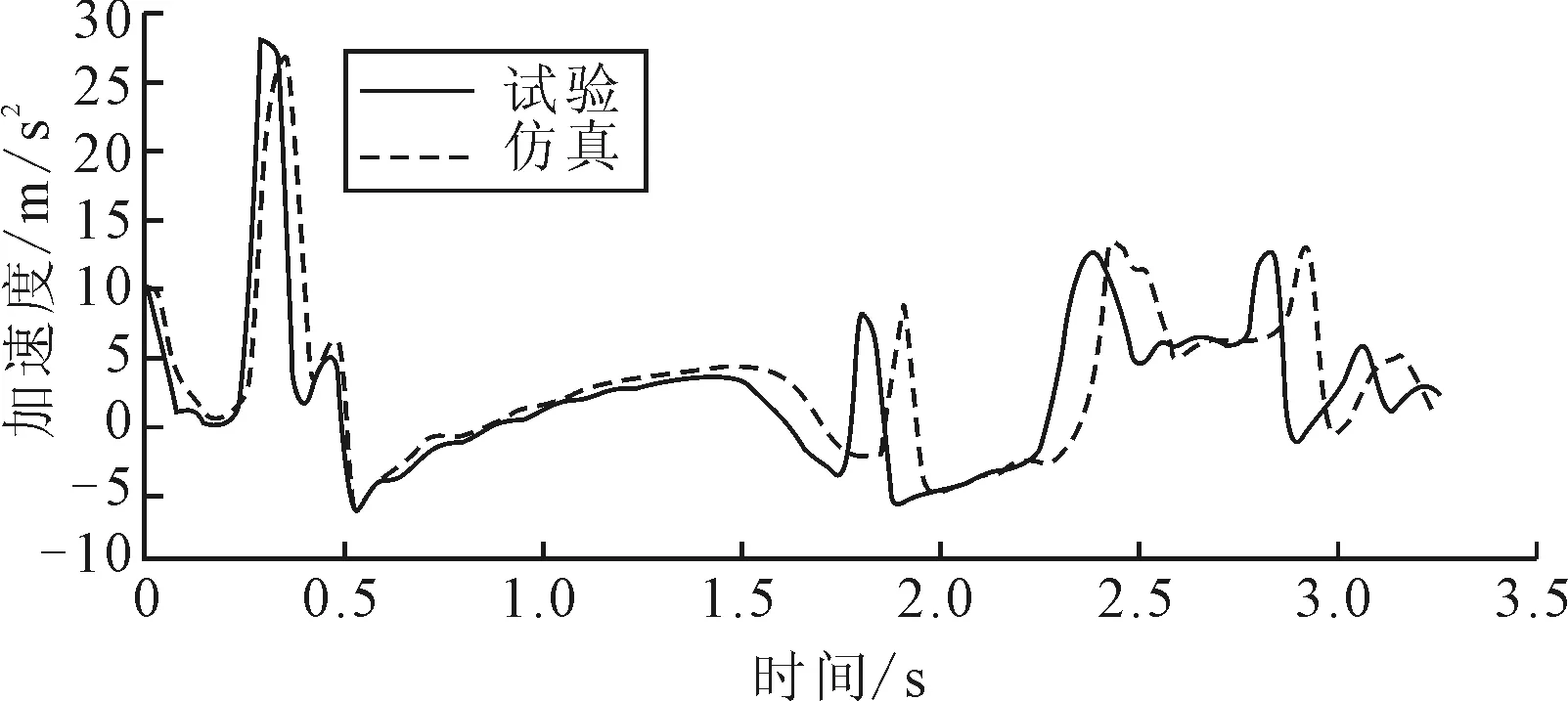
图4 仿真与试验加速度对比

综上所述，对比试验与仿真模型整车翻滚状态以及加速度曲线之间的误差可以得出：仿真模型具有足够的精度，可代替实车进行仿真分析及优化设计。

2 安全带约束系统优化设计

2.1 假人损伤评价指标

汽车翻滚过程中，乘员因为受到冲击载荷作用，头部、胸部及颈部极易发生损伤。参考C-NCAP中假人伤害评价指标，WIC正则化伤害评估值被广泛应用于正碰工况下的假人损伤评价，WIC计算公式如式(1)所示。

(1)

式中：HIC36(Head Injury Criterion)为头部伤害指标。C3ms和CCOMP分别为胸部3 ms合成加速度值和胸部压缩量评价指标，均为假人胸部伤害评价的重要指标。Fleft、Fright分别代表左右大腿骨轴向圧力。

由于平台翻滚不同于正碰，腿部的伤害较小而头部更容易受到车身上边梁的冲击从而导致颈部严重受伤，因此，笔者不考虑腿部受到的伤害，选取头部伤害指标HIC36、胸部3 ms指标C3 ms、胸部压缩量CCOMP以及颈部伤害指标即颈部最大轴向载荷Fz作为安全带约束系统约束性能的优化目标。将头部伤害指标HIC36值、胸部3 ms加速度值C3 ms、胸部压缩量CCOMP及颈部最大轴向力Fz这4个评价指标作为子优化目标，依据C-NCAP法规中各个评价指标对应的最大值作为比例因子，使用加权系数法将多目标优化问题转化为单目标优化问题，考虑头部、胸部和颈部伤害的综合评价指标f(X)如式(2)所示。

(2)

式中：Fz为颈部最大轴向力。

2.2 安全带约束系统优化设计

对汽车安全带约束系统工程优化问题而言，多刚体模型进行计算比较耗时。常采用构造简单的显式函数作为近似模型代替耗时的仿真模型[7-8]。因此笔者使用最优拉丁超立方抽样对设计变量在样本空间中抽取一定数量的样本点，构建Kriging近似模型，并结合多岛遗传算法对安全带约束系统特性参数进行优化。优化设计流程如图5 所示。

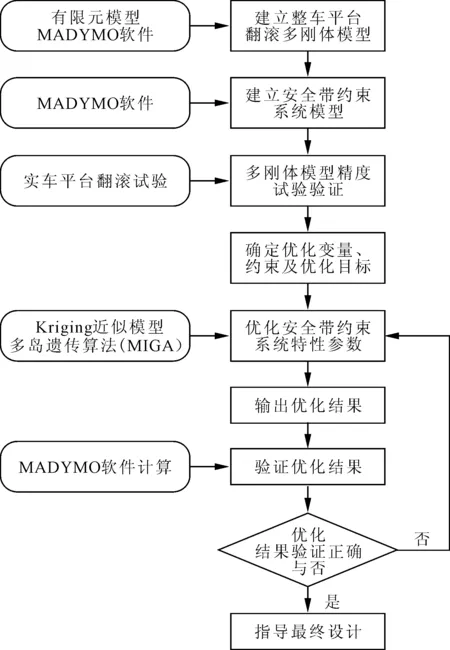
图5 安全带约束系统优化设计流程图

安全带约束系统约束效能主要体现在对人的保护，故将综合评价指标f(X)作为优化目标，使用加权系数法将多目标优化问题转化为单目标优化问题。依据C-NCAP法规对4个子评价指标设置响应的约束条件，考虑到仿真模型存在一定的误差，因此，本数学模型各伤害评价指标约束的阈值略低于法规要求；将MADYMO软件中定义的安全带伸长率曲线缩放系数、安全带的上挂点高度以及初始应变作为设计变量。根据公司规定以及车身实际尺寸给出设计变量的边界条件。优化问题的数学模型可描述为：

(3)

式中：f(X)为综合评价指标；gHIC为人体头部损伤HIC36值；gC3 ms为胸部损伤3 ms加速度值；gCCOMP为胸部压缩量峰值；gFZ为颈部轴向力峰值；X为设计变量，其中，x1为安全带伸长率曲线缩放系数；x2为安全带上挂点距整车重心所在水平位置的高度；x3为安全带初始应变。

2.3 试验设计方法

这里试验设计方法采用最优拉丁超立方设计。拉丁超立方设计(Latin Hypercube Design, LHD)由McKay等首先提出，该方法能够随机抽取规定的若干各点，并且能够保证每一个因子的每个水平只出现一次。然而拉丁超立方设计在试验点分布的均匀性上存在缺陷，随着水平数的增加，设计空间的部分区域会丢失。针对这一缺陷，最优拉丁超立方设计(Optimal Latin Hypercube Design, Opt LHD)改进了拉丁超立方设计的均匀性。均匀性的改进使得近似模型的构建相较于拉丁超立方设计更加精确。

优化问题中的设计变量个数为3，理论上构建Kriging近似模型需要的样本点数至少为7个。构建模型用到的样本点数越多，模型精度越高。考虑到近似模型精度和计算总耗时等因素，利用ISIGHT软件，采用Opt LHD方法对设计变量进行抽样，抽取了40个试验点，并利用MADYMO软件对40个试验点进行了计算，分别得到40个样本点的头部伤害指标HIC36值、胸部3 ms加速度值C3 ms、胸部压缩量CCOMP及颈部轴向力Fz，部分抽样结果及仿真结果如表2所示。

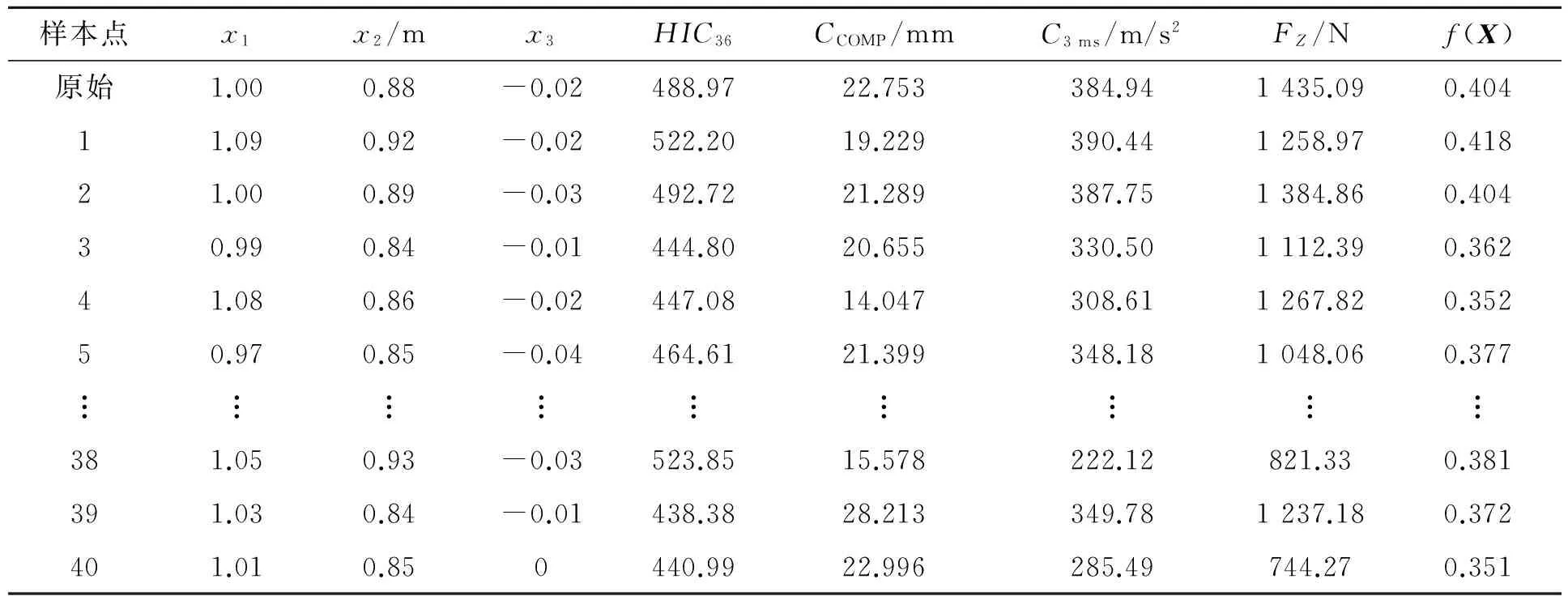
表2 试验设计样本值及仿真结果

2.4 Kriging近似模型

Kriging方法又称空间局部插值法，是以变异函数理论和结构分析为基础，在有限区域内对区域化变量进行无偏最优估计的一种方法[9]。

对40组样本点在ISIGHT软件中对4个约束及设计目标(综合评价指标)分别构建Kriging近似模型。拟合类型(Fit Type)选择收敛速度更快的各向同性Isotropic类型。相关函数选择精确度更高的Matern Cubic函数。构建的Kriging近似模型3D图能在后处理中得到。其中，设计变量x1、x2、x3与综合评价指标f(X)之间的关系如图6所示。

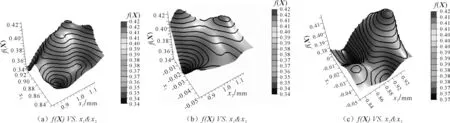
图6 Kriging近似模型3D后处理

Kriging近似模型构建完成后还需要另取样本点来对近似模型的精度进行验证，以确保近似模型的有效性。一般常采用均分方根差(RMSE)和平均相对误差(RAAE)来评价模型精度[10]。计算公式如式(4)和式(5)所示。

(4)

(5)

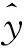
表3 Kriging近似模型精度验证

2.5 多岛遗传算法

多岛遗传算法(Multi-Island Genetic Algorithm，MIGA)由Kaneko等对并行分布遗传算法(Parallel Distributed Genetic Algorithms，PDGAs)进行改进，相比于传统的遗传算法，该算法具有更优的全局寻优能力和更快的求解效率。

笔者在ISIGHT软件中，选取多岛遗传算法对所构建的Kriging近似模型在给定的设计变量范围及约束范围内进行寻优。子种群规模设置为10，岛的个数设置为10，总进化代数设置为20，交叉概率设置为0.8，变异概率设置为0.01，岛间迁移率设置为0.5。每次进化需要对每个岛上所有个体进行计算，共进化20代，因此总的计算次数为2 000。种群进化过程如图7所示。最优解个体出现于图示虚线相交处。

最终，由多岛遗传算法得到最优设计结果为：安全带伸长率曲线缩放系数x1取0.92；安全带上挂点距整车重心所在水平位置的高度x2取0.86；安全带初始应变x3取-0.03。由Kriging近似模型得到的响应值分别为：头部伤害指标HIC36值为395；胸部3 ms加速度值为C3 ms为313.93 m/s2；胸部压缩量CCOMP为21.959 mm；颈部最大轴向力Fz为1 176.6 N；综合评价指标为0.331 43。

3 优化结果及分析

获得最优设计结果后需要将设计参数代入多刚体模型中进行计算以验证优化方案的有效性，并将优化方案与原始设计方案进行对比。

3.1 优化结果误差验证

为验证优化方案的有效性和准确性，将最优设计方案在多刚体模型中进行修改并提交计算，并评价其与近似模型估计值之间的误差。仿真结果与模型预测值之间的误差分析如表4所示。

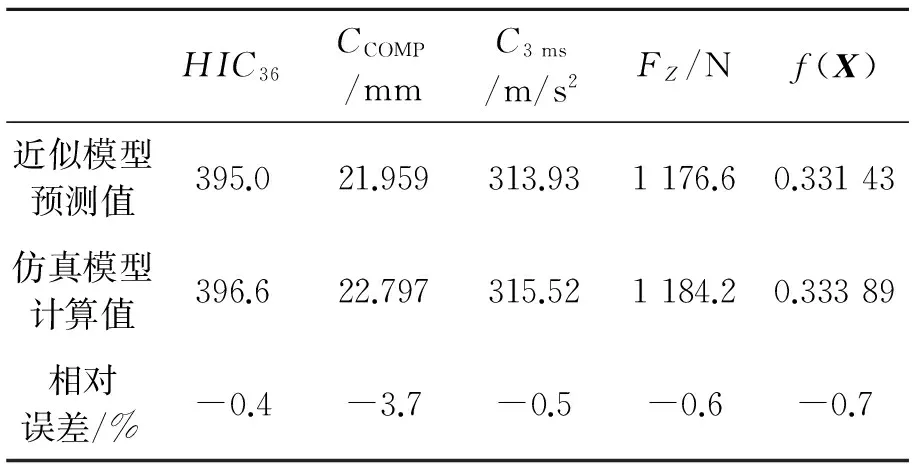
表4 优化方案误差分析

通过误差分析可以发现，仿真结果与近似模型预测结果的目标值之间最大相对误差为-3.7%，并未超过±5.0%，满足误差要求，说明该优化方案具备足够的精度，能够在一定程度上指导最终设计。

3.2 优化结果分析

将优化方案的仿真输出结果与初始设计目标值进行对比，各个子目标和综合目标值结果的优化幅度如表5所示。表5中优化幅度为正值，说明优化方案相比于原始方案有提升。

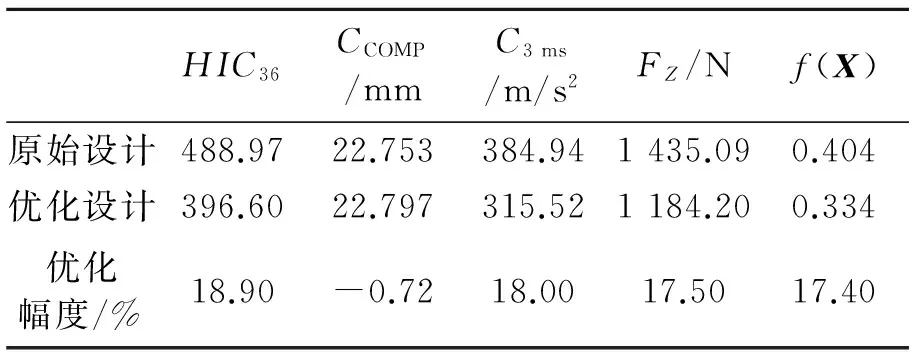
表5 优化幅度分析

通过分析优化结果可以发现，除了胸部压缩量峰值CCOMP比原始设计稍差，其他的假人评价指标均相比于原始设计有较大的提升。其中头部伤害指标HIC36相比于原始设计优化幅度最大，其优化幅度为18.9%。综合评价指标f(X)的优化幅度为17.4%，优化效果明显。

4 结论

通过建立带假人和安全带约束系统的整车多刚体模型，选择安全带伸长率曲线缩放系数、安全带上挂点距整车重心所在水平位置的高度、安全带初始应变作为设计变量，将头部伤害指标HIC36、胸部3 ms伤害C3 ms、胸部压缩量CCOMP以及颈部最大轴向载荷Fz这4个子评价指标运用加权系数法构建综合评价指标，将多目标优化问题转化为单目标优化问题，以综合评价指标作为安全带约束系统约束性能的优化目标。通过Opt LHD方法进行仿真试验设计并构建Kriging近似模型，将复杂工程问题转化为精度较高的数学模型。通过优化各设计变量，使得头部伤害指标HIC36下降18.9%、胸部3 ms伤害C3 ms指标下降18.0%、颈部最大轴向载荷Fz下降17.5%。该研究成果可对汽车翻滚碰撞安全带约束性能的优化设计起到一定指导作用，在后续研究中会对悬架部分和整车上部结构进行精细化建模，使得多刚体模型能够反映上部结构的变形从而得到更加精确的仿真结果。

[1] 莫易敏,徐东辉,刘昌业.微型汽车平台翻滚试验仿真研究与影响因素分析[J].汽车技术,2016(11):56-61.

[2] Chengyue Jiang, Neal-Sturgess C E, Yuanzhi Hu. Kinematics Simulation and Head Injury Analysis for Rollovers Using MADYMO[J]. International Journal of Crashworthiness, 2010,15(5):505-515.

[3] 洪亮,葛如海,周海超,等.正面碰撞安全带约束系统保护效果的研究[J].广西大学学报(自然科学版),2016,41(2):363-370.

[4] Chou C C,Wu F. Development of MADYMO-based Model for Simulation of Laboratory Rollover Test Modes[C]∥Proceedings of the 19th International Technical Conference on the Enhanced Safety of Vehicles (ESV).Washington,DC:[s.n.],2005:1031-1043.

[5] Albrodt S B, Tahan F, Digges K. Evaluation of Different Roof Strength Methods in Quasi-Static and Dynamic Rollover Tests Using Finite Element Analysis of a 2003 Ford Explorer Model[C]∥SAE 2014 World Congress & Exhibition. [S.l.]:[s.n.],2014:675-681.

[6] 莫易敏，梁永彬，刘昌业，等.某微车平台翻滚试验与有限元仿真研究[J].数字制造科学，2017，15(1-2)：12-18.

[7] 刘鑫,吴钢,尹来荣.基于近似模型管理的汽车安全带约束系统优化设计[J].振动与冲击,2016,35(6):132-136.

[8] 赖宇阳.Isight参数优化理论与实例详解[M].北京:北京航空航天大学出版社,2012.

[9] 崔杰,张维刚,谢伦杰,等.基于kriging代理模型的碰撞安全性稳健性分析[J].汽车工程,2013,35(1):51-55.

[10] 张君媛,林逸,华伟,等.基于随机模拟的汽车安全带系统约束效能优化[J].汽车工程,2004,26(3):311-313.