某SUV动力传动系统扭振问题分析
2017-03-12袁守利刘志恩
尹 凡,袁守利,刘志恩
(1.武汉理工大学 现代汽车零部件技术湖北省重点试验室,湖北 武汉 430070;2.汽车零部件技术湖北省协同创新中心,湖北 武汉 430070)
随着经济社会的快速发展,越来越多的人把汽车作为代步工具。相应地,人们对汽车的性能要求也越来越高,而振动和噪声是影响乘坐舒适性的重要因素。一般来说,汽车内外的噪声和传动系统的故障大部分都是由汽车发动机和传动系的扭转共振引起的[1],因此,对汽车传动系进行扭振特性分析与研究是十分必要的。
笔者基于多体动力学理论和力学原理,对某前置后驱式SUV汽车动力传动系统扭振固有特性进行模型简化、参数确定和模型建立,计算分析发现发动机与传动系统在56.4 Hz附近发生扭转共振现象。基于动力传动系统的扭振机理,通过对传动系统组成部件的敏感参数进行分析研究,从而提出了改善传动系扭振问题的优化方案。
1 问题描述
根据某汽车公司提供的资料可知,该公司某前置后驱式SUV汽车在三档全油门加速工况中,明显感觉到其低速抖动现象比较严重。经过前期的实车试验以及驾驶员和乘客的主观感受,初步判断引起该车低速抖动的原因是动力传动系统的扭转振动比较严重。为了提高该SUV汽车在市场的竞争力,改善该车在加速工况下低速抖动的现象,利用AVL EXCITE Designer软件建立了汽车动力传动系的扭转振动模型。
2 动力传动系扭振模型简化原则
在前置后驱式汽车中,发动机输出的动力通过传动系传递到驱动车轮。在这个过程中,传动系会受到来自发动机、路面和传动系自身多种因素的影响,导致汽车传动系产生复杂的扭转振动。由于汽车传动系的结构比较复杂,很难直接计算各组成部分的转动惯量、扭转刚度和阻尼,使得传动系的扭转振动很难计算。因此,有必要采用多体动力学理论和力学原理,对传动系进行简化,在简化模型上进行扭振分析。
进行模型简化时,遵循以下基本原则[2]:
(1)传动系各部件的扭转刚度和转动惯量是影响传动系扭振特性的主要因素,因此,采用集中质量方法和当量原则对传动系进行合理的简化,等效换算出传动系各部件的转动惯量和扭转刚度,进行快速建模仿真。这就是传动系仿真分析采用的多自由度“质量—弹簧—阻尼”的离散化建模方法。
(2)对于转动惯量较大的旋转零部件,模型简化为作用在旋转中心的刚体集中质量。
(3)基于多体动力学,将曲柄连杆机构简化为多个具有转动惯量的集中质量点,两集中质量点之间由扭转刚度连接。
(4)弹性连接部分,简化为两个刚体集中质量及连接刚度,两个集中质量分别为主动部分和被动部分,连接刚度为两个刚体集中质量间的当量刚度。
3 动力传动系扭振模型建立
笔者采用AVL EXCITE Designer软件对汽车传动系进行建模分析计算。根据用户提供的汽车传动系的数模,建立如图1所示的整车动力传动系三档扭振模型。
在软件模型中,所研究的传动系被划分为44个自由度的扭振模型。三档稳态工况下的扭振模型如图2所示。
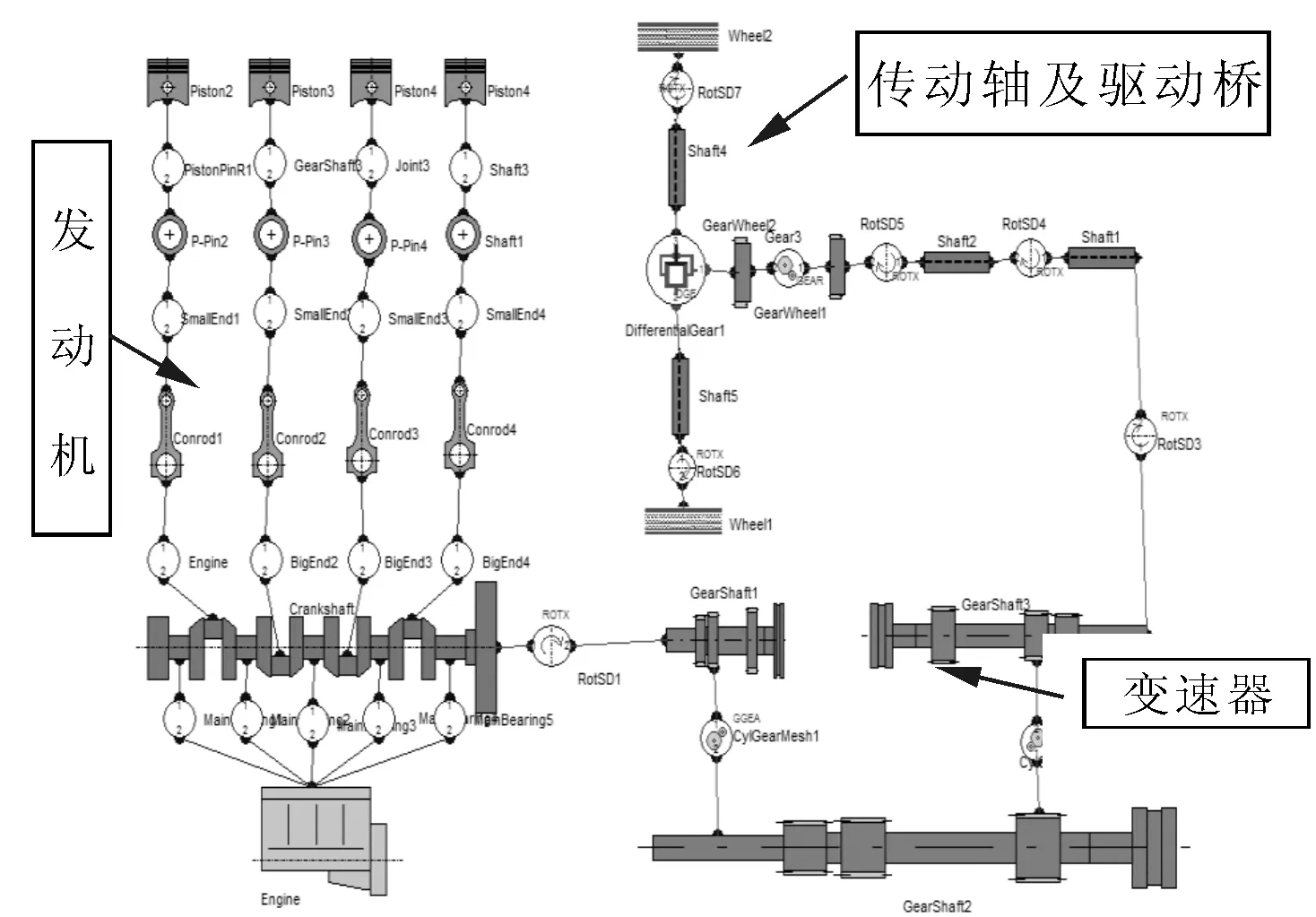
图1 整车动力传动系三档扭振模型
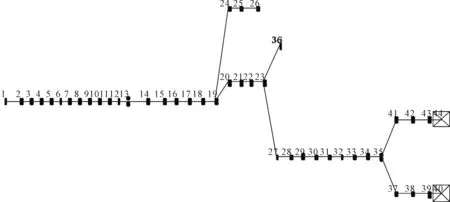
图2 三档稳态工况下的动力传动系扭振模型
图2中各部分自由度对应的动力传动系统各组成部分如表1所示。

表1 扭振模型中自由度对应的动力传动系统组成
3.1 建立发动机扭振模型
发动机是汽车动力的源头。在汽车行驶时,发动机不断地为汽车提供动力,必然会引起传动系的扭转振动。对发动机扭振模型进行适当简化,建立了如图3所示的发动机扭振模型。模型描述如下:①主要反映曲柄连杆机构;②不考虑轴承细节特征和止推轴承;③几何参数来自AutoCAD及CATIA测量;④曲柄和平衡块的扭转刚度利用有限元方法计算得到,即利用Hypermesh软件进行前处理,再用Nastran求解器计算得到;⑤发动机缸压曲线为GT-POWER中仿真导出的数据。其中,曲轴扭振模型如图4所示。

图3 发动机扭振模型
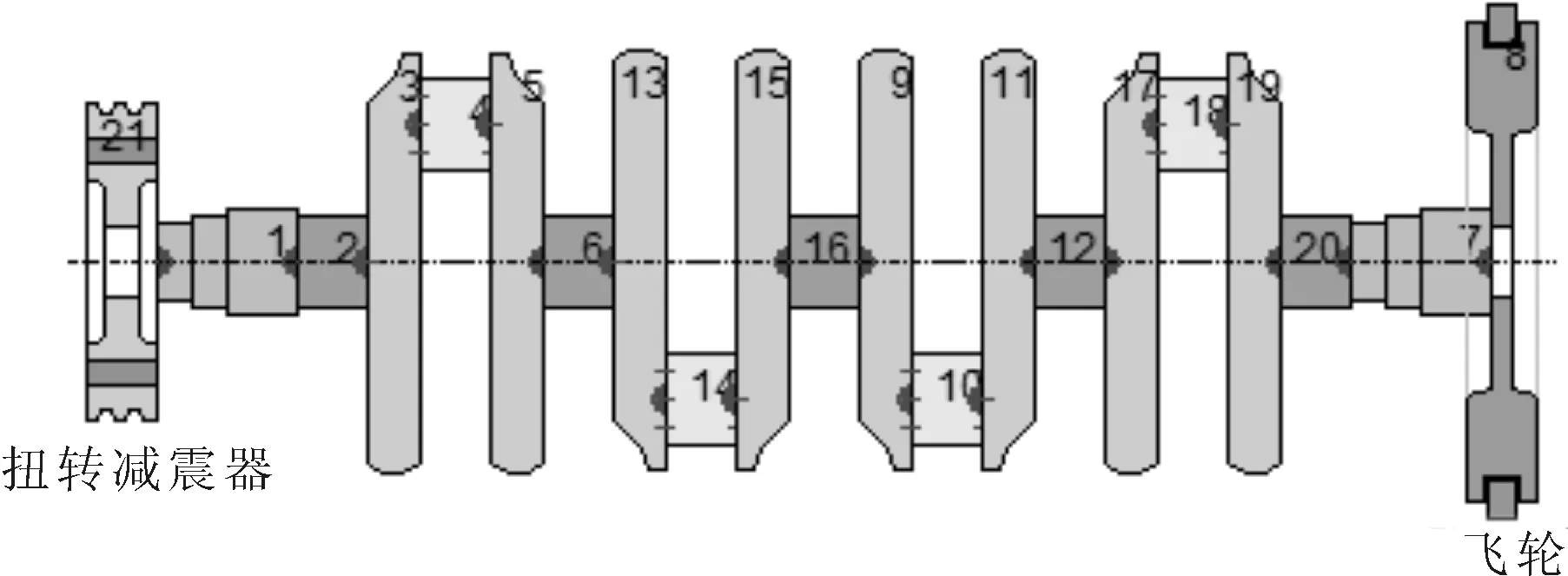
图4 曲轴扭振模型

图5 变速器扭振模型
3.2 建立变速器扭振模型
变速器是传动系的重要总成之一。所研究车型的变速器为五档手动变速器。主要分析传动系扭振,因此只需要将齿轮和轴简化为扭振模型。图5为简化得到的变速器扭振模型。模型描述如下:①RotSD1模拟离合器扭转减振器扭转刚度和阻尼,用两对齿轮副模拟常啮合齿轮和第三档齿轮;②认为齿轮没有弹性,只计算转动惯量;③按变速器三维模型,提取出轴系、齿轮、同步器系统,同时对轴系进行分段,分段时考虑同步器、齿轮和轴承的位置;④在CATIA中测量出分段后各部分转动惯量,得出等效轴尺寸,折合原则为转动惯量相等轴向尺寸不变;⑤不考虑轴承细节特征和润滑条件。
3.3 建立传动轴与驱动桥扭振模型
汽车动力从变速器输出轴输出后,经过传动轴传递到主减速器、差速器、半轴,最后到车轮。图6为简化后的传动轴与驱动桥扭振模型。模型描述如下:①认为万向节的转动惯量远大于传动轴的转动惯量;②RotSD3为变速箱输出轴与传动轴之间的连接,RotSD4和RotSD5 为万向节,GearWheel1和GearWheel2分别为主减速器的主、被动齿轮;③根据提供的三维模型测出万向节的转动惯量,并将其等效到与其相邻的轴段上(pully1、pully2),万向节的阻尼值直接赋到RotSD4和RotSD5 中;④根据三维模型,通过有限元软件(Hypermesh & Nastran)计算得出各连接处的刚度;⑤车轮惯量为整车质量换算值;⑥由于所研究车型属于发动机前置后驱,传动轴比较长,因此将传动轴分成两段。
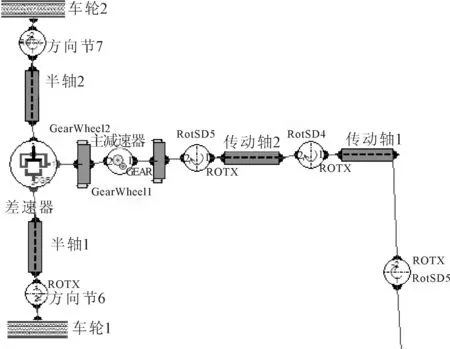
图6 传动轴与驱动桥扭振模型
4 模型计算及结果分析
基于该SUV汽车动力传动系三档扭振模型,进行扭振模态分析,重点关注其频率分布和第二根传动轴的扭振振型等。
整车动力传动系三档的扭振模态如图7所示。由图7可知,传动系一阶模态频率为7.8 Hz,二阶模态频率为56.4 Hz,三阶模态频率为296 Hz,四阶模态频率为311 Hz,五阶模态频率为581 Hz。
由于四冲程四缸机的激励扭矩主要为二、四、六、八阶,并且随着激励阶次的增加,激励的幅值迅速减小,即激励能量迅速减小,因此,对第二阶激励进行控制就可以达到较好的扭振控制效果[3]。该车型发动机常用转速为800~3 000 r/min,对应第二阶激励频率为26.7~100 Hz。由图7可知,传动系第二阶模态频率为56.4 Hz,因此,传动系统在此工况下存在共振的情况。

图7 整车传动系三档扭振模态
从图8所示的第二根传动轴输出端的角速度波动可以看出,当发动机转速在1 685 r/min左右时,传动系统的第二根传动轴出现一个转速波动峰值,对应的频率为56.2 Hz左右。由此可以说明,发动机在此工况下的危险转速是1 685 r/min,因为第二阶扭振激励频率(56.2 Hz)与传动系扭振系统第二阶固有频率(56.4 Hz)发生了共振,导致第二根传动轴在此共振区附近发生了较大的转速波动。共振现象的发生,对传动系统的危害很大,并且严重影响了整车的乘坐舒适性。
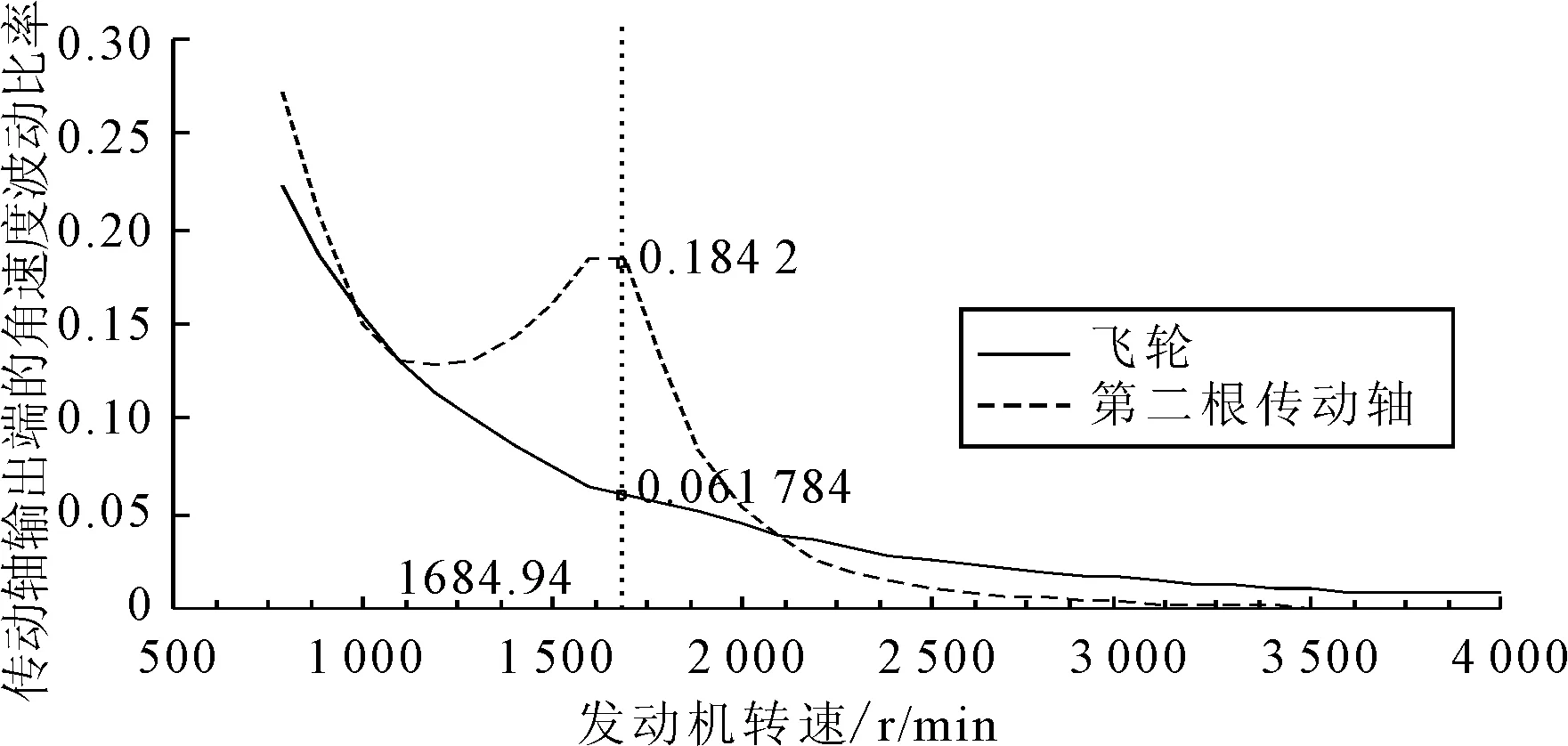
图8 第二根传动轴输出端角速度波动
5 拟优化方案
5.1 传动系统扭振机理分析
汽车动力传动系统是一个复杂的多自由度扭转振动系统,当外界激励的频率与动力传动系统扭振系统的频率一致时,就发生了扭转共振[4-5]。
发动机激励、路面激励、传动轴振动激励等因素是车辆行驶过程中引起传动系扭振的主要因素[6]。路面对汽车的影响可以通过改善道路条件得到缓解,为了最大程度地控制汽车动力传动系统的扭转振动,重点应该放在源头以及传递路径上。汽车动力系统扭转振动的源头是发动机,传递路径包括离合器、变速箱、传动轴系以及驱动桥等,笔者研究的重点是传递路径。
对于发动机扭转振动的传递路径控制,首先可以采用将单质量飞轮改为双质量飞轮。双质量飞轮由三部分组成,即第一质量(初级飞轮)、第二质量(次级飞轮)和两质量之间的减震器。通过调整双质量飞轮内部的扭转刚度和初级飞轮、次级飞轮的转动惯量,从而改变动力传动系的扭振固有特性,避免共振的产生,具有良好的减震效果[7-8]。其次,还可以考虑的有离合器扭转刚度、传动轴转动惯量和刚度以及在传动轴末端加装扭转减震器。在传动系扭振系统中,离合器的转动惯量相对于整个系统转动惯量而言很小,而离合器的扭转刚度和阻尼与传动系其他零部件相差较大。因此,离合器的转动惯量对传动系扭振系统的固有特性不敏感,而离合器的扭转刚度和阻尼对传动系扭振系统的固有特性比较敏感[9]。
传动轴作为主减速器的振动激励,其振动必然会影响后桥的振动与噪声。由于传动轴自身的结构特点以及装配形式的差异,必然会在传递转矩过程中产生复杂的振动,这些振动将导致传动轴输出端的转矩产生波动,从而对主减速器的振动噪声产生影响[10]。因此,传动轴的转动惯量和刚度影响也比较大。除了可以对传动轴本身的转动惯量和刚度进行调节外,也可以考虑在传动轴末端加装扭转减震器,利用减震器的衰减振动的作用,达到减小振幅的作用[11]。
5.2 优化方案分析
由于传动系扭振系统在二阶模态频率为56.4 Hz(发动机危险转速1 685 r/min)附近发生了共振现象,导致第二根传动轴发生了较大的转速波动,对传动系危害较大。因此,必须对该传动系统进行优化,目标是尽量降低传动系扭振系统的二阶模态频率至30 Hz(对应发动机转速900 r/min)以下。
通过对传动系统扭振机理的分析可知,可能影响传动系统二阶扭振模态的敏感参数有:离合器的扭转刚度和阻尼;齿轮啮合刚度;传动轴扭转刚度;改单质量飞轮为双质量飞轮等。
5.2.1 方案1—改变离合器扭转刚度
离合器的扭转刚度对传动系扭振系统的固有特性比较敏感。下面将分析离合器扭转刚度对传动系扭振系统的影响。
原模型的离合器扭转刚度为11.7 N·m/deg,根据供应商可以提供的离合器型号,现将离合器刚度分别改为6.7 N·m/deg,8.7 N·m/deg,15.7 N·m/deg,20.7 N·m/deg。基于传动系三档扭振模型,计算得到离合器扭转刚度的改变对传动系扭振影响的变化规律。表2为不同离合器扭转刚度下整车传动系的扭振模态频率。
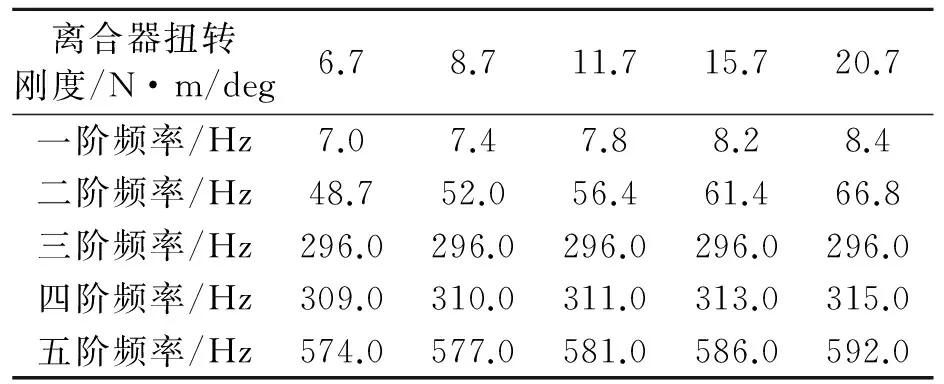
表2 不同离合器扭转刚度下的传动系扭振频率
由表2可知,当离合器扭转刚度减小时,传动系第一阶固有频率依次减小,但减小幅度较小;传动系第二阶固有频率也依次减小,减小幅值较大,达到13.7%;第三到第五阶固有频率基本不变。
图9为不同离合器扭转刚度下的第二根传动轴输出端的转速波动随发动机转速的变化曲线。由图9可知,当离合器扭转刚度减小时,传动轴第二根轴输出端的危险转速减小,转速波动基本不变;当离合器扭转刚度增大时,传动轴第二根轴输出端的危险转速增大,转速波动基本不变;当离合器刚度从11.7 N·m/deg减小到6.7 N·m/deg时,危险转速由1 680 r/min左右降到1 400 r/min左右。
因此,可以得到结论:离合器扭转刚度是传动系扭振系统的敏感因素,在离合器扭转刚度满足使用要求的情况下,可以通过减小离合器的扭转刚度,减小发动机的危险转速,并减小传动轴第二根轴的转速波动,从而改善第二根传动轴的扭振情况。

图9 第二根传动轴的转速波动
5.2.2 方案2—改变齿轮啮合刚度
齿轮啮合刚度是齿轮啮合时的扭转刚度,等于扭转载荷和齿轮体总的弹性旋转角度之比。从前面分析可知,齿轮啮合刚度也可能是影响传动系扭振模态的敏感参数。原模型变速器三档齿轮啮合刚度为2e8 N/m,现将其齿轮啮合刚度分别改为2e6 N/m、2e7 N/m、2e9 N/m、2e10 N/m,基于传动系三档扭振模型,计算得到齿轮啮合刚度的改变对传动系统扭振的影响的变化规律。表3所示的是不同齿轮啮合刚度下整车传动系的扭振模态频率。
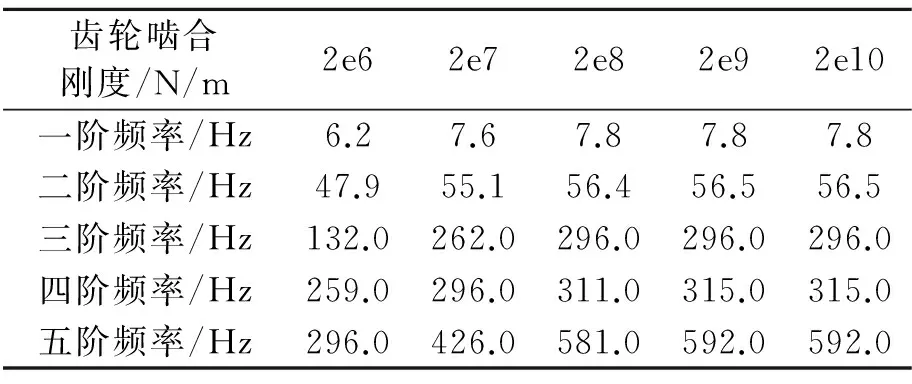
表3 不同齿轮啮合刚度下的传动系扭振频率
由表3可知,当齿轮啮合刚度在2e6~2e8 N/m之间时,随着齿轮啮合刚度减小,传动系第一、二、三阶固有频率都下降;当齿轮啮合刚度在2e8~2e10 N/m之间时,传动系各阶固有频率基本不变;当齿轮啮合刚度下降到2e6 N/m时,二阶固有频率下降到47.9 Hz,减小幅值达到15%。
图10为不同齿轮啮合刚度下的第二根传动轴输出端的转速波动随发动机转速的变化曲线。由图10可知,齿面啮合刚度在2e6~2e8 N/m间减小时,转速波动减小,危险转速略有下降;齿面啮合刚度在2e8~2e10 N/m间变化时,转速波动略有减小,危险转速基本不变。
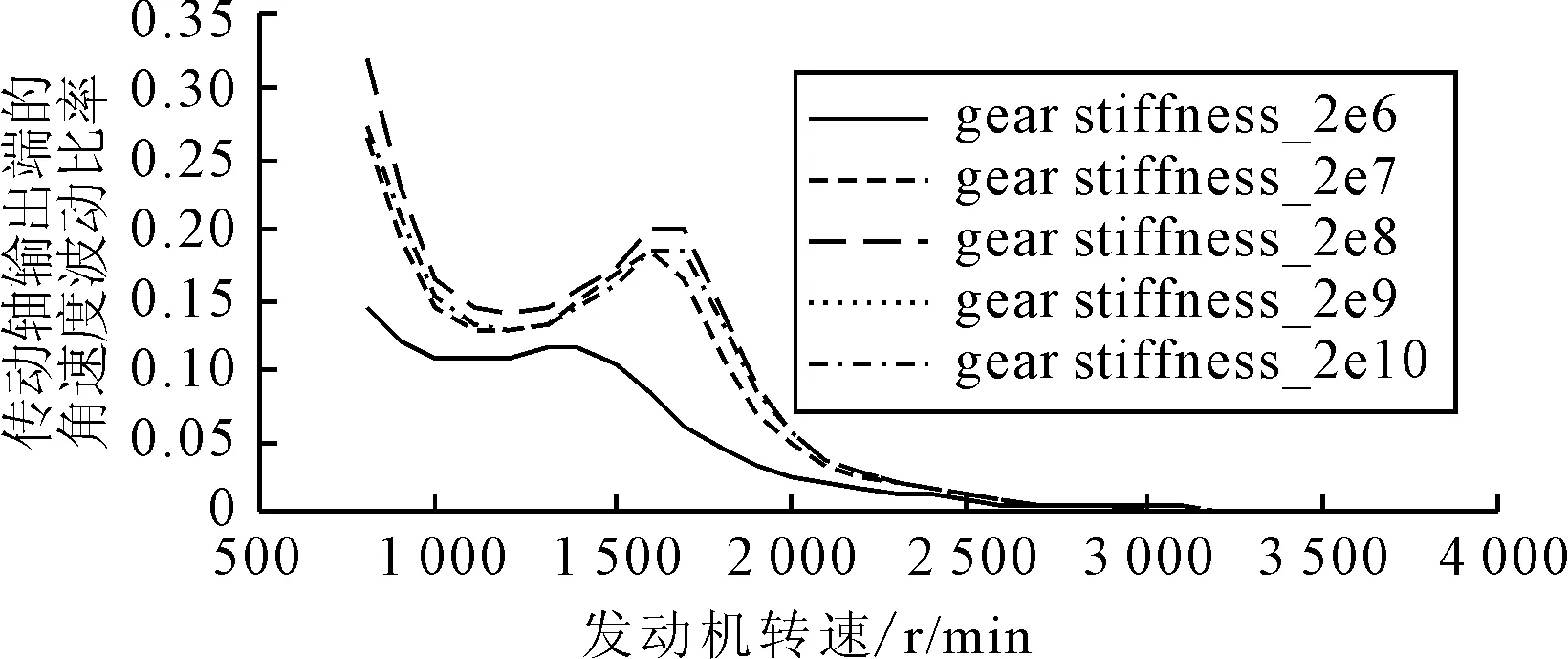
图10 第二根传动轴的转速波动
因此,可以得到结论:齿轮啮合刚度是传动系扭振系统的敏感参数,在变速器齿轮的啮合刚度满足使用要求的情况下,可以通过改变变速器三档齿轮的啮合刚度,减小发动机的危险转速,并减小传动轴第二根轴的转速波动,从而改善传动轴第二根轴的扭振情况。
5.2.3 方案3—双质量飞轮
原车型采用的是单质量飞轮,其转动惯量为0.074 kg·m2。现采用双质量飞轮代替单质量飞轮,将原单质量飞轮一分为二,通过改变其初级飞轮与次级飞轮的转动惯量配比,计算得到飞轮的改变对整车传动系统影响的变化规律。次级飞轮转动惯量分别为第一级转动惯量的80%、90%、100%、110%和0%(无次级飞轮)。表4为不同情况下的整车扭振模态频率。
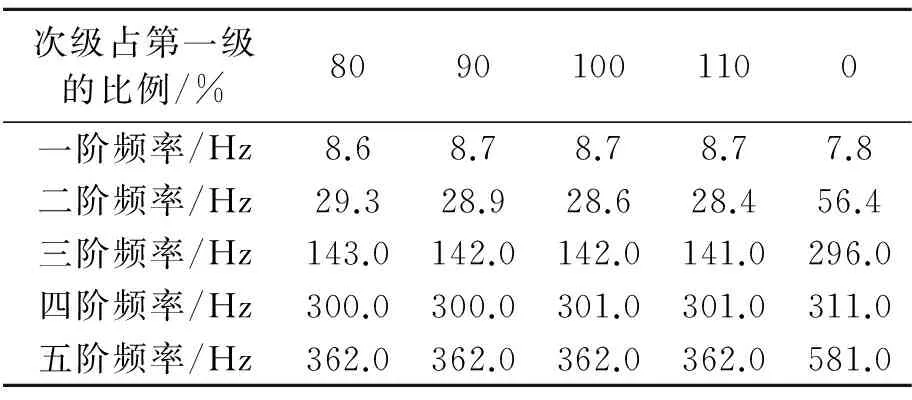
表4 不同飞轮下的传动系扭振频率
由表4可知,增加双质量飞轮后,第一、第二、第三和第五阶固有频率降低效果显著,减小幅值最大达到48%,对第四和第六阶固有频率基本没影响;当第二级飞轮转动惯量由80%向110%增大时,对各阶固有频率基本没影响;当第二级飞轮转动惯量为80%时,危险转速在900 r/min左右,可以避开发动机的激励频率。
因此,可以得到结论:飞轮的转动惯量是传动系扭振系统的敏感参数,将单质量飞轮改成双质量飞轮,可以将传动系统的二阶扭振频率降低到29 Hz左右,可以避开发动机的激励频率,从而改善传动轴第二根轴的扭振情况。
6 结论
根据以上对整车传动系统扭振情况的敏感参数的研究与分析,为了降低发动机的危险转速(即主要降低整车传动系统二阶扭振模态频率),改善传动系统第二根传动轴的扭振情况,提出了以下几个优化方案:
(1)在离合器的扭转刚度满足条件的情况下,减小离合器的扭转刚度,可使二阶频率最高降幅达到13.7%,从而适当降低发动机的危险转速。
(2)在变速器齿轮啮合刚度满足条件的情况下,降低齿轮啮合刚度,可使二阶频率最高降幅达到15%,从而适当降低发动机的危险转速。
(3)将单质量飞轮一分为二,用双质量飞轮代替单质量飞轮,可使二阶频率最高降幅达到48%,从而显著降低发动机的危险转速,改善动力传动系统的扭振情况。
笔者所作的问题分析与优化方案的提出都是基于理论与仿真进行的,如果只考虑三个方案的优化效果,方案3是最好的;如果只考虑三个方案的可执行空间,方案3是最好的;但是如果考虑到成本的话,方案1和2有一定的优势。因此,在实际的工程项目中,需要综合考虑多种因素,采用最合适的优化方案。
[1] 张玉伦.多轴驱动汽车动力传动系统扭振固有特性及其随机性分析[D].长春:吉林大学,2015.
[2] 宋武强.基于EXCITE-Designer的车用汽油车曲轴扭转振动分析和不同减震器性能对比[J].内燃机动力与装置,2010(1):21-24.
[3] 吕振华,冯振东,程维娜,等.汽车传动系扭振噪声的发生机理及控制方法述评[J].汽车技术,1993(2):1-4.
[4] 王东,闫兵,王东亮.汽车传动系扭振引起的车内轰鸣声控制方法[J].噪声与振动控制,2015(4):73-76.
[5] BEIN T, ELLIOTT S J, FERRALLI L, et al. Integrated Solutions for Noise & Vibration Control in Vehicles[J]. Procedia Social and Behavioral Sciences, 2012,48:919-931.
[6] 舒歌群,高文志,刘月辉.动力机械振动与噪声[M].天津:天津大学出版社,2008.
[7] 程海峰.基于整车传动系的双质量飞轮的结构设计与性能优化[D].长春:吉林大学,2011.
[8] Demin C,Yueyin M,Wei S,et al. Research of Design and Vibration Reduction of the Dual Mass Flywheel with Arc Helix Spring[C]∥Proceedings of 2011 International Conference on Electronic & Mechanical Engineering and Information Technology (Volume). Harbin:Harbin University of Science and Technology IEEE Press,2011:2706-2709.
[9] 郑若元.摩擦离合器结构参数对车辆传动系统振动的影响分析[D].广州:华南理工大学,2015.
[10] Zhang J, Ma B, Zehn M. Study on Clutch Engagement Judder during Launch Process for Dual Clutch Transmissions[J]. International Journal of Vehicle Noise and Vibration, 2010,6(2):176-199.
[11] 彭波.可变不连续性传动轴对后桥主减振动噪音特性影响的研究[D].武汉:武汉理工大学,2013.
