基于运动目标三维轨迹重建的视频序列同步算法

王雪 SHI Jian-Bo PARK Hyun-Soo 王庆

视频同步,又称视频对准,是计算机视觉领域中一个重要的基础问题.根据同步方式不同,现有的视频同步方法可分为基于外触发脉冲的同步和基于视频图像序列中视觉特征的同步.其中,基于外触发脉冲的同步技术作用在相机端,多用于控制多相机同步实现高速图像采集存储,硬件成本较高;基于视觉特征的同步算法通过分析图像序列中的同步线索实现多个视频间的时域对齐,可用于行为识别、基于内容的视频检索及非刚性结构三维重建等视觉任务.本文主要讨论基于视觉特征的视频同步方法,其常规思路是联合优化图像序列间的空间和时间对准.空间对准多指在待同步帧对的二维图像或三维相机坐标系下计算某种几何变换,因此依赖精确的特征提取和匹配.时域对准通过估算图像序列间的线性或非线性时域映射以获得最优的空间对准.

为了降低问题求解的复杂度,研究者们提出各种假设来减少待估计参数的数量.假设静止相机或联合运动相机,则空间变换关系恒定不变.现有方法多在二维图像坐标系中估算几何变换,如单应[1−2]、仿射变换[3]、射影变换[2−6]等,并利用重投影误差来度量空间对准的程度.由于求解基础矩阵对噪声敏感,Rao等[7]针对透视模型提出一种基于对极几何的秩约束.进一步地,Tresadern等[8]综合单应、仿射变换和射影变换三种几何模型下的亏秩条件,提出了统一的算法框架.这类方法多用于窄基线条件下图像点轨迹及对应关系已知的视频对准.为克服宽基线条件下特征匹配难的问题,文献[9−10]提出一种弱假设,即观测序列中像点的空间位置可以用参考序列中像点子集空间位置的线性组合描述,且该线性关系维持不变.这样,算法不再依赖已知的像点对应关系,各序列中的像点甚至可以对应不同的空间点.缺点是该方法仅适用于固定仿射相机间的常量偏移时域同步.假设相机沿相似轨迹运动[11−15],则对应帧的相机坐标系可近似认为原点重合,仅对应坐标轴间存在较小的旋转角度.因此,内容上越相似的两幅图像帧,其时域同步的可能性越高.基于这种思想,Wang等[16]提出了一种基于SIFT特征点匹配的视频同步算法,并提供友好的交互界面允许用户手动设置入点、出点或剪辑标记来同步多机位序列.值得一提的是,这种交互方式也是众多视频编辑工具实现多机位序列同步的方式,此外还包括使用基于音频的同步来准确对齐剪辑,例如Edius、Premiere等.假设时域映射关系为线性,例如常量偏移模型[4,9−10],或者一维仿射模型[1−2,5,7],则时域映射关系可以用一个简单的参数化模型tr=ρto+∆来描述,其中tr和to分别表示参考序列和观测序列中的图像帧索引,ρ为两序列的帧率比,∆为帧索引偏移常量.

联合空间和时间对准能够提高系统的鲁棒性,但这类方法面临两个主要的挑战.1)对于独立运动相机和包含多个运动目标的三维动态场景(图1)来说,基于几何变换的空间对准是十分困难的.2)考虑到丢帧、时域连续性等问题,线性时域映射不再满足需求,而非线性时域映射的估算会增加现有算法求解的复杂度.

图1 待同步的第一人称视角图像序列Fig.1 Video sequences captured by fi rst-person cameras

针对独立运动相机,Tuytelaars等[17]提出一种基于反向投影的同步方法,用于弱透视投影模型下视频间的偏移常量时域同步,通过将图像点反向投影到空间中的一条线,从而将时域对准问题转换为在空间中寻找相交或距离最短的直线问题.Lei等[18]基于三视图几何约束建立时间轴图,用于多个图像序列间的偏移常量时域同步.这些方法都假设线性时域映射关系,并且依赖精确的特征点跟踪和匹配,因此在实际应用中受到限制.Dexter等[19]利用图像序列的自相似矩阵为每帧图像计算时域自适应的特征描述,通过时域运动特征匹配实现图像序列对的非线性时域同步.该算法利用场景中静止的背景点估计全局运动实现相机自运动补偿,仅适用于平面场景或远视角.

本文提出一种针对独立运动相机的视频时域对准算法,其主要想法是利用空间中运动目标的轨迹(时间空间特征)来同步图像序列.取代传统的帧对空间对准,我们在时间轴上从单帧的图像点延长到持续整个子序列段的图像点轨迹,通过三维运动轨迹重建,提出一个基于轨迹基系数的秩约束用于度量任意子序列对的空间对准程度.随后,本文提出一种基于图的非线性时域对准算法,用于搜索最优时域映射关系.进一步地,我们将该算法从双序列对准扩展到多序列的情况.最后,本文在仿真数据和真实第一视角数据集上进行验证.

1 双序列时域对准

1.1 基于三维轨迹重建的线性时域对准

当两个或多个相机相对静止,或者沿相似轨迹运动,空间中同一个运动点在不同相机拍摄的图像序列中的二维轨迹是相似的.然而,若相机自由运动,则上述结论不再成立.为了消除相机自运动对目标运动分析的影响,我们可以在二维图像空间中尝试相机自运动补偿,或者将二维观测反投影回三维空间中进行运动分析.后者的优点是受场景及相机运动限制较小.本文采取后一种方法,首先利用文献[20−21]提出运动目标三维轨迹重建算法恢复运动目标的三维轨迹.

令摄像机在第t帧的投影矩阵为P(t)∈R3×4,按透视射影变换将空间中一点X(t)=[X(t)Y(t)Z(t)]T投影到二维像点x(t)=[x(t)y(t)]T,根据相机成像模型有

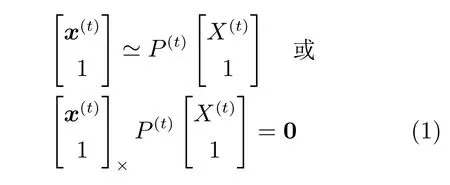
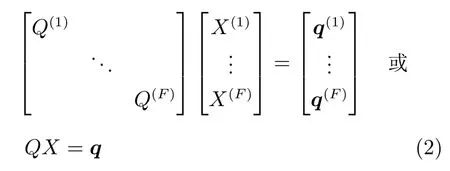
其中,X=[X(1)T,···,X(F)T]T为重建的运动目标三维轨迹.假设轨迹可以采用离散余弦变换(Discrete cosine transform,DCT)基以较少的低频分量线性表示.

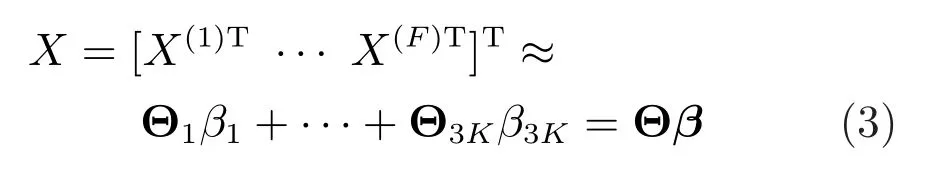
如果该目标的三维轨迹同时被另外一台摄像机捕捉到,类似地,我们可以得到

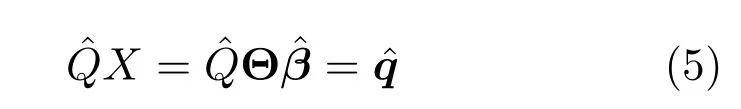
为了提高公式的易读性,本文用相同符号加角号表示与第二个图像序列相关.由于Θ是正交矩阵,基系数β和理论上应相同.若空间中有P个点同时被两个摄像机看到,当满足不等式3K≥2P时,基系数矩阵的秩最大不超过P.若两序列同步,M的秩减小,相反,若两序列不同步,则M的秩增加.因此,我们可以通过比较不同偏移量下M的秩,来估算时域映射关系.值得注意的是,P不是一个上确界,这取决于P个点间的刚性约束关系.无论如何,基系数矩阵M的秩在同步时的下降量不低于非同步时的下降量.

令Sr={Ir(1),Ir(2),···,Ir(Nr)}和So={Io(1),Io(2),···,Io(No)}分别表示由独立运动相机拍摄的参考图像序列和观测图像序列,其中Nr和No分别为两个序列的帧数.可检验的整数时间偏移量∆的取值范围是R=[−No+F,Nr−F].

在上述关于秩约束的推导中,我们用到了三个假设:1)视频间的图像点对应已知;2)图像点跟踪持续整个图像序列;3)视频间的时域关系为常量偏移模型.本节先讨论第一个假设,其余两个假设在下一节中进行论述.

若视频间的点对应关系未知,我们可以使用一个弱假设[9−10]令秩约束仍然成立:观测序列中跟踪点对应的三维点,其空间位置可以用参考序列中所有跟踪点对应的三维点集的子集的线性组合描述,即满足下列关系

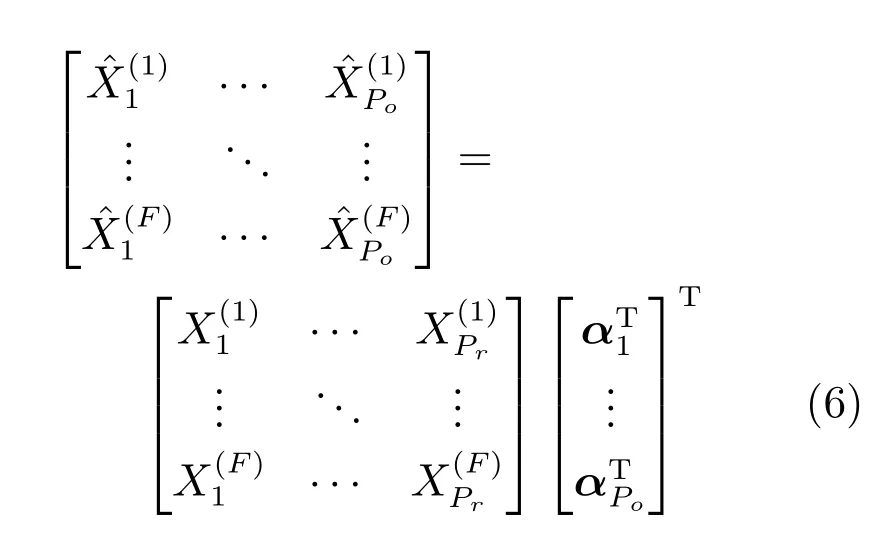
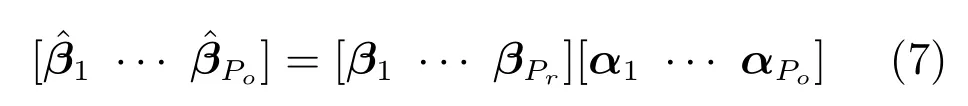
同理,当满足不等式3K≥Pr+Po时,新基系数矩阵的秩最大不超过Pr.引入这一弱假设的好处是,在省去了估计视频间图像点对应的同时,还使得该算法能够处理宽基线条件下的视频同步,即被两个相机同时看到的三维点数量有限或者为零.

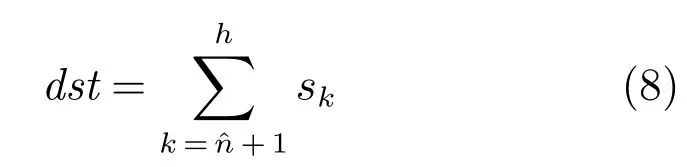
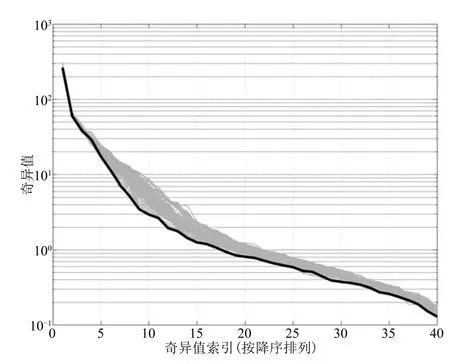
图2 测试序列对同步和不同步时基系数矩阵 的奇异值Fig.2 An example of the singular values of in synchronized case and non-synchronized cases

进一步地,我们将距离函数dst转换为归一化的代价函数c.

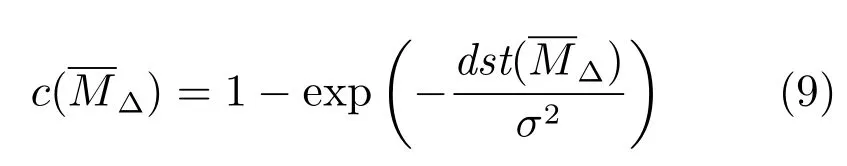
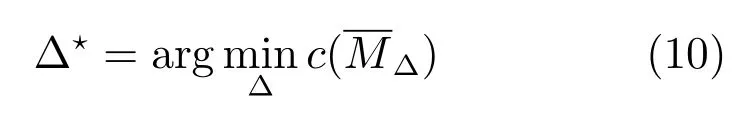
1.2 非线性时域对准

上述算法虽然不依赖视频间已知的像点对应,但仍然假设图像点跟踪持续整个图像序列.实际应用中,由于遮挡、光线局部变化等原因,多数跟踪算法很难维持长时间的精确跟踪.此外,假设视频间时域关系为一维常量偏移模型,这也限制了同步算法的适用范围.为此,本文提出一种能够利用不同长度图像点轨迹的非线性时域对准算法.

我们将Sr和So分别划分为若干F帧长的子序列段,令每个子序列段的中间帧为参考帧.然后针对候选子序列对(fr(j),fo(k)),选择跟踪持续fr(j)的Pr个图像点和跟踪持续fo(k)的Po个图像点,重建这些点的三维轨迹并计算基系数矩阵.其中,fr(j)表示Sr中参考帧为Ir(j)的子序列,fo(k)同理.最后利用代价函数c估算(fr(j),fo(k))的对齐程度,记为cjk.这样,我们得到代价矩阵,其中是地板函数.

Pr和Po的确定依据以下两个规则:1)以参考图像序列为例,将持续跟踪子序列段fr(j)的图像点个数记为Pr(j),则.对Po同理.2)满足两个不等式,2F≥3K和3K≥Pr+Po.前者为了确保运动目标轨迹重建时的超定系统,后者则保证了的秩最大不超过Pr.

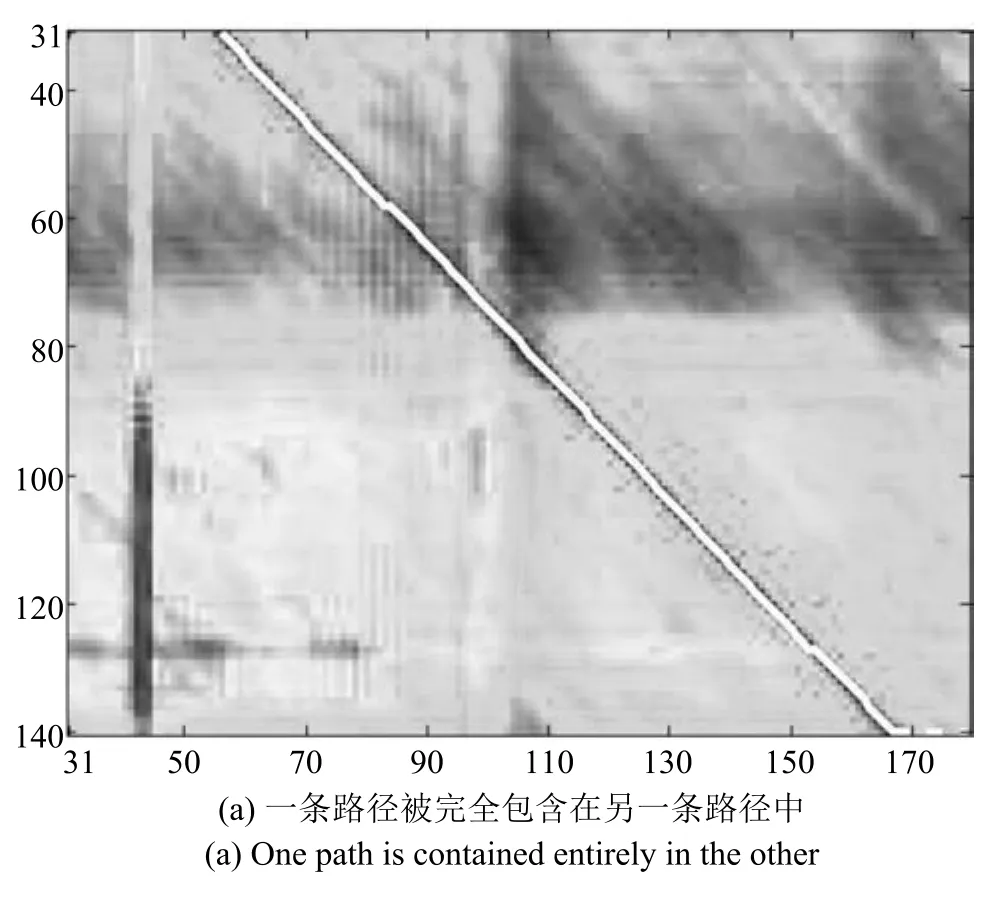
式(6)的成立基于常量时间偏移模型的假设,即tr=to+∆.当图像序列对的帧率不同但相近,或者存在轻微的丢帧现象时,该等式仍然近似成立.由此,相较于不同步的子序列对,由时域同步或者最相近的子序列对构造的基系数矩阵仍然具有较小的秩.非线性时域关系可以用一个离散映射函数ω(to)=tr,to=1,···,N表示,其中N≤No,表示观测序列中有N帧图像在参考序列中有时域对准的图像.该函数在基于图的方法中为经过代价矩阵的一条路径.为了应对局部时域重叠,受文献[16]的最优路径搜索算法启发,首先,我们基于Dijkstra算法计算候选路径集,每一条候选路径可以开始和结束于参考序列或观测序列的任何帧,该路径的代价为其经过代价矩阵中各节点值加和的平均值.然后,基于候选路径集选择最优路径.为了避免选择长度过短的路径,根据路径结束于Sr或者So,我们将候选路径集划分为两个池,分别在每个池中选择最小代价路径.多数情况下,一条路径被完全包含在另一条路径中(图3(a)),这时我们选择较短那条作为最优路径.若两条候选路径不重叠(图3(b)),则选择较长那条作为最优路径.图中代价矩阵的横轴和纵轴分别表示Sr和So的帧索引,其元素的颜色越深,对应值越小.

图3 代价矩阵和最优路径(白实线)Fig.3 Cost matrix and optimal path(white solid curve)

双序列时域对准算法的具体流程如图4所示.其中跟踪二维点轨迹和重建三维轨迹都是针对单个图像序列独立执行的,唯一需要联合双序列的步骤是估算代价矩阵和最优路径.注意,我们分别选择fr(j)中的Pr个点和fo(k)中的Po个点进行三维轨迹重建,然后计算(fr(j),fo(k))的对齐代价,这一步骤需要重复T次,最后取中值作为最终的cjk.通常地,当Pr和Po值一定时,重复次数越多,算法鲁棒性越好,相应地,时间复杂度越高.非线性时域对准算法的时间复杂度为O(Nr×No×T).试验中,我们根据跟踪结果的精度和跟踪点数量决定T.一般地,跟踪结果越准确,跟踪点数越少,T值越小.若已知时域映射为线性或常量偏移模型,可以利用线性时域对准算法使时间复杂度降为O(Nr+No).

2 多序列时域对准

理论上,我们可以将上述双序列时域对准算法简单地扩展到多序列的情况,即增加代价矩阵的维度,并搜索最优映射p:R→RD,其中D为待同步图像序列的数量.然而在实际应用中,这种方法是不可取的.假设有五个待同步的序列,每个序列以30fps的帧率持续10秒,即有300帧图像.那么代价矩阵的元素数量达到3005.若采用32位浮点数存储这个代价矩阵,需要约8.8TB的内存.这显然已经超出了现有的硬件支持能力.本文采用文献[16]中基于最小生成树(Minimum spanning tree,MST)的方法寻找双序列对准集合,将多对多(Allto-all)的多序列时域对准问题简化为只利用最优的双序列对准获取全局的时域映射变换.

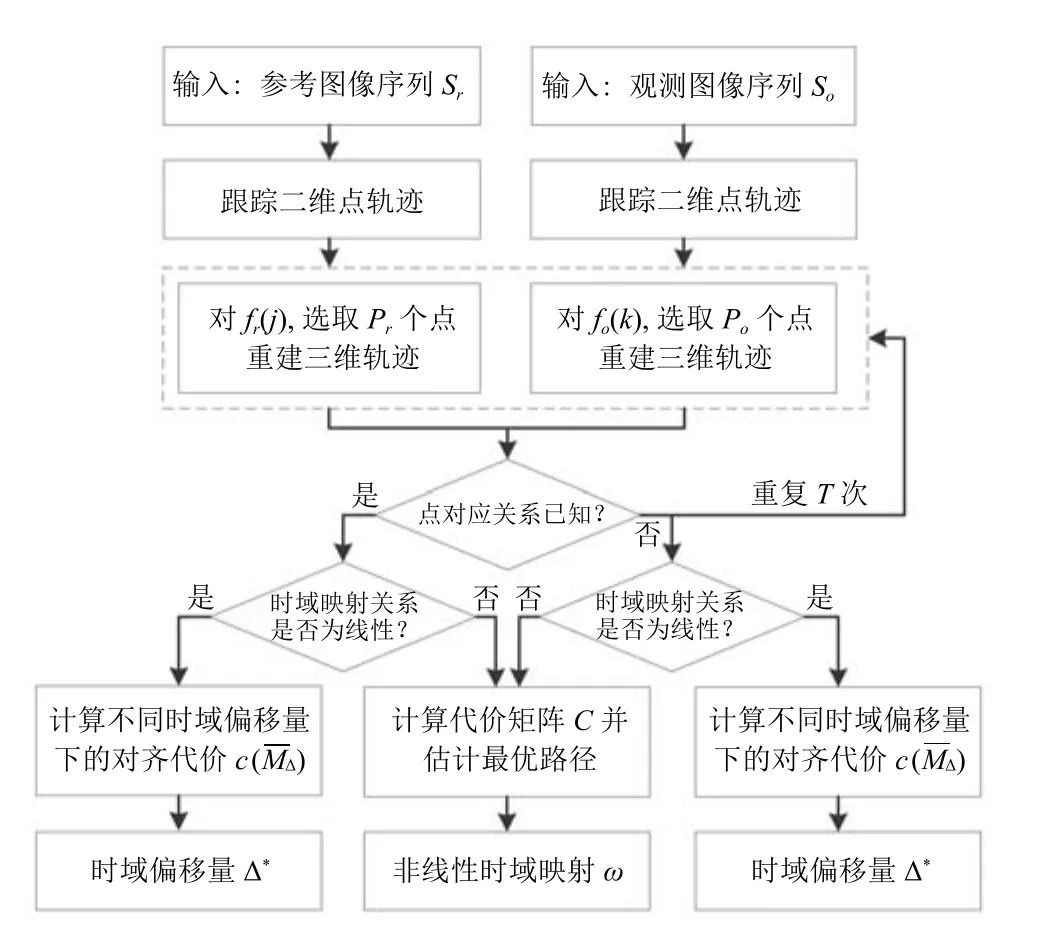
图4 双序列时域对准算法流程图Fig.4 The fl ow chart of pairwise alignment

3 仿真实验

本文基于文献[21]提供的人体运动捕捉数据(倒地、站立和步行)生成仿真数据.通过随机合成相机投影矩阵,将13个人体关节点的三维运动轨迹投影到两组不断变化的图像平面上.重建后的三维运动轨迹及其真实值如图5所示.我们将其中一个图像序列作为参考序列,将另外一个图像序列时域偏移∆ 帧后,再随机去掉若干帧(丢帧率不高于5%),作为观测序列.每组实验重复10次,每次采用不同的随机相机运动轨迹.该实验中所有二维点轨迹均持续完整的图像序列,计算代价矩阵时令采样次数T=1.本文采用原始DCT基重建三维轨迹,令每个维度上基的数量K=30.

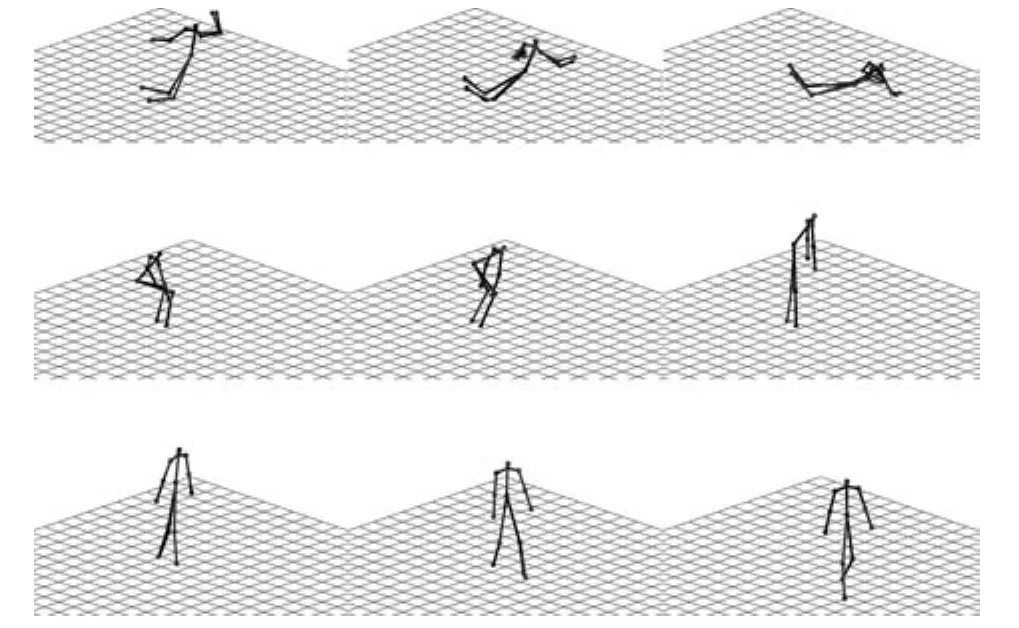
图5 仿真数据重建结果(黑)和真实值(灰)Fig.5 Reconstruction(black)and ground truth(gray)of simulated data

3.1 鲁棒性

为了验证跟踪误差、数据丢失和图像点数量对新算法精度的影响,我们设置了如下三组实验.如不做特殊说明,认为无数据丢失.1)不同跟踪误差和子序列段长度与时域对准误差间的关系,结果如图6(a)所示.从图中可以看出,子序列段越长,算法受跟踪误差影响越小,其同步精度越高.但是,延长子序列段会缩小代价矩阵,相应地,时域映射关系中自变量的取值范围变小,表现在图中就是最优路径变短.注意,像素单位的跟踪偏移误差是通过用跟踪误差级α乘上一个服从标准正态分布的伪随机数得到.2)造成跟踪过程中目标数据丢失的原因有遮挡、自遮挡、度量失败等.图6(b)为不同程度的数据丢失(0%,5%,10%)与时域对准误差间的关系.只要跟踪到足够多帧数的观测值能确保三维轨迹重建时的超定系统,新算法的精度基本不受数据丢失的影响.3)不同图像点数量与时域对准误差间的关系,结果如图6(c)所示.理论上,如果一个三维点的运动足够快并且随机,它被两个独立运动的相机同时捕获到,那么仅用这一个点就可以同步两个相机.实际应用中考虑到单个点重复性运动的情况,加入空间相对位置关系的约束,综合多个位于不同刚性物体上的点能大大提高时域对准的精度.

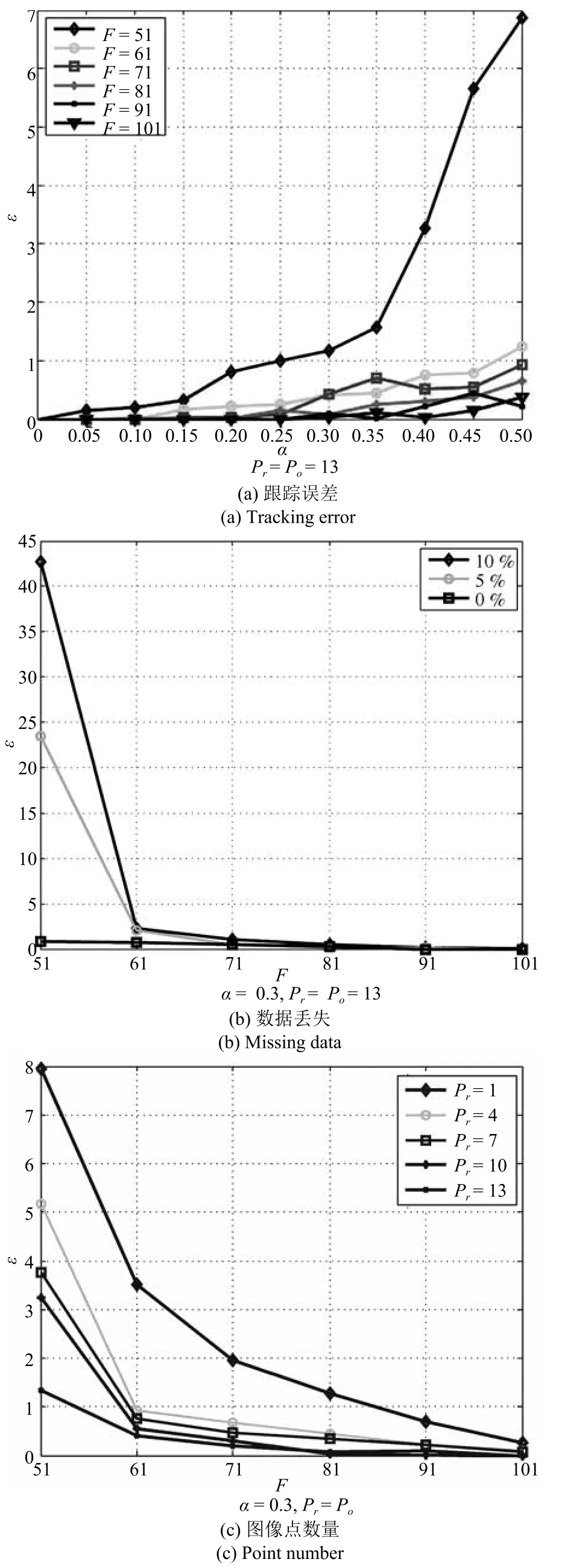
图6 跟踪误差、数据丢失和图像点数量对同步结果的影响Fig.6 Comparisons of robustness with regard to tracking error,missing data and point number

3.2 准确性

本文在仿真数据基础上对比了本文方法与现有方法的时域同步精度,包括文献[17]中基于反向投影的方法BPM 和文献[8]中基于透视模型对极几何的方法ECM.其中,BPM用到3组不同的对应点集,每组点集包含5个图像点.这两种方法均假设线性时域映射关系,为了对比公平,在它们计算代价矩阵的基础上,利用本文提出的基于图的最优路径搜索算法,寻找非线性时域映射函数.

除上述两种方法外,我们还提出以下对比基准.基于不同序列重建对应点的三维运动轨迹,当观测序列和参考序列精确同步时,同步帧索引的空间点重合;当观测序列和参考序列为子帧级别同步时,即帧和帧之间的时域偏移量为非整数,则同步帧索引的空间点距离最小.因此,我们将新算法中基于秩约束的时域对齐度量准则替换为基于三维重建点距离的度量准则,记为PDM.

图7(a)为步行数据集上各算法受跟踪误差影响的时域对准精度曲线图,是仿真数据集上各算法试验结果对比.随着跟踪误差逐渐变大,本文算法表现出更好的鲁棒性.ECM方法的时域对准误差与跟踪误差不成正比,这可能归结于试验中的非线性时域映射,相比原始方法的线性时域映射假设,非参数模型大大增加了解空间的维度,导致当输入有噪声时该算法的准确度降低.图7(b)～7(i)是针对倒地数据集中一个测试序列对(常量偏移量∆=35)各算法的同步结果.图7(b)～7(e)为没有跟踪误差时,各算法计算的代价矩阵和最优路径.图7(f)～7(i)为当跟踪误差级α=0.30时,各算法计算的代价矩阵和最优路径.注意,与本文算法基于子序列对计算代价矩阵不同,三种对比方法均计算任意帧对的时域对齐程度,生成代价矩阵的维度为No×Nr.

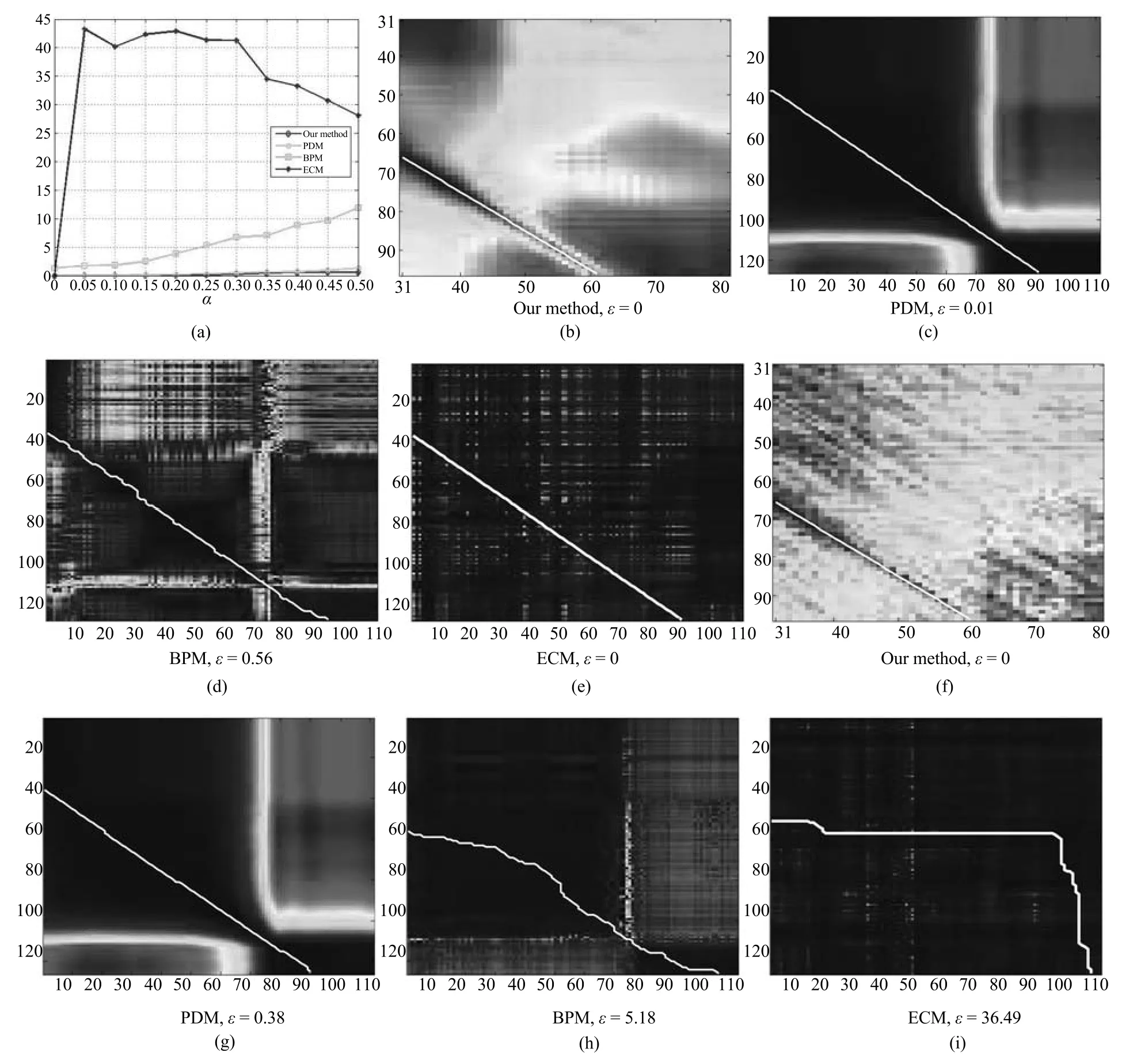
图7 仿真数据集上各算法在不同跟踪误差下的实验结果对比以及估算的代价矩阵示例Fig.7 Comparisons of alignment accuracy using different methods regarding tracking noise level and representative cost matrices with estimated optimal paths superimposed

4 第一人称视角数据

为了验证新算法在实际应用中的性能,我们提出一个基于第一人称视角的社交场景视频数据集,包括积木、健身毯、篮球和玩具火车四个场景.其中,前两个场景记录了4个5～6岁儿童的交互式行为,篮球场景记录了两组成年球员之间的5 vs 5对抗性比赛,玩具火车场景是简单的刚体运动.对象在场内可以自由运动,固定在其头部的GoPro相机以第一人称视角拍摄整个动态场景,相机运动可近似认为相互独立.区别于一般监控相机通常采取固定的位置和视角,以第三人称视角从场景外部向场景内部进行拍摄,第一人称视角相机是从场景内部佩戴者的视角出发“观察”场景,通过不断变换位置或姿势获得对感兴趣目标的持续最佳观测视角.每个场景的数据包括多个图像序列,单个图像序列持续时间约5～10秒,伴随着相机平移运动约3～12米,绕光轴旋转运动约20～60度.

数据采集时,所有相机被设置到相同的拍摄模式,例如图像尺寸、帧率等.前期我们利用FFmpeg工具包从同一场景的不同视频源文件中提取图像帧作为测试序列.该试验中,参考序列和观测序列的生成帧率分别为48fps和46fps.我们利用外置闪光灯在数据采集开始时、采集中(多次)和采集结束时标记若干同步帧,并手动同步余下帧,以此作为视频序列同步的真实值.

对于包含关节人体的场景,本文采用双粒度跟踪算法[23]获取二维点轨迹,其优势在于能够跟踪到大量位于人体躯干及四肢靠近上端部位的点,从而确保其空间位置线性相关假设的成立.另外,该算法提供了一个控制空间采样率的参数,可以避免像点分布过于集中.缺点是基于稠密光流估计的点轨迹计算开销较大.在玩具火车场景中,我们利用KLT算法[24]跟踪特征点轨迹.基于跟踪算法的输出结果,我们需要选择位于运动目标上的点轨迹,并去掉长度过短以及明显错误的轨迹.除上述自动跟踪点轨迹外,我们还手动标记运动目标上若干特征点的二维运动轨迹.由于遮挡导致某特征点不可见时,我们根据前后相继帧以及辅助视角推测当前帧中该特征点的位置.由于超出视角范围导致特征点不可见,我们则不做标记.

本文利用运动恢复结构算法[25−27]估计每一帧相机的空间姿态.图8展示了对各场景的三维重建结果,包括相机轨迹、静态场景和部分运动点轨迹.在积木和健身毯场景中,我们试图同步三个图像序列.其中,相较于2号图像序列,3号图像序列和参考图像序列的相机视角差别更大,相机朝向几乎相反的方向.本文用#1和#2分别表示各场景中的两组测试序列对.

图8 三维重建结果(从左到右对应场景依次为:积木,健身毯,篮球#1,篮球#2和玩具火车)Fig.8 The 3D reconstruction results(From left to right:block building,exercise mat,basketball(#1),basketball(#2)and toy train.)

在重建空间点的运动轨迹时,如果相机运动缓慢,其运动轨迹也可以用DCT基的线性组合表示,这会导致轨迹重建的精度降低[21].由于不同时刻的图像集合可以模拟相机的快速随机运动,为了提高轨迹重建的质量,我们引入非测试用图像序列辅助轨迹重建,并人工标注对应点.

除了仿真实验中提到的三种方法,这里还额外对比了两种基于二维特征的方法:基于二维运动特征的方法MFM[16]和基于SIFT特征匹配的方法SMM[19].表1列出了各算法在真实数据集上的归一化时域对准误差ε(式(11)),除玩具火车场景外,本文算法在各测试序列对上的同步误差最小.当自动跟踪点数量较少或者不满足空间位置线性相关假设时,本文算法的同步精度下降.这时,可以通过添加手动标注图像点轨迹的方法提高同步质量.由于SMM假设同步帧在图像内容上最相似,从而不适用于宽基线条件下的相机同步,在积木和健身毯场景中的同步误差较大.图9～13展示了不同场景中各算法的帧同步结果,各算法的输入图像点叠加显示在对应图像帧上,空白表示观测序列中不存在同步帧.由于空间有限,这里仅给出了本文算法在自动跟踪点轨迹输入下的同步结果.试验中令K=30,F=81,λ=0.99.关于有效秩定义中阈值λ的取值,图14给出了本文算法在积木#1上的一组对比结果.图14(a)为不同有效秩对同步结果的影响,图14(b)～14(e)是不同有效秩对应的代价矩阵.当λ＜0.99时,同步结果的精度出现明显下降.而当λ越接近于1时,同步结果的精度越好.

由于本文算法只适用于帧率相同或者相近的图像序列对,帧率相差越大,秩约束越弱.图15对比了不同帧率比时本文算法的同步误差.图15(a)为不同帧率比对同步结果的影响.图15(b)～15(d)是当观测序列帧率分别为46fps、40fps和24fps时的代价矩阵,图中最优路径的估算值和真实值分别用实线和虚线标识.试验中我们令参考图像序列的生成帧率为48fps,仅改变观测图像序列的帧率.当帧率比接近于2时,序列同步时基系数矩阵具有较小秩的特征几乎不明显.

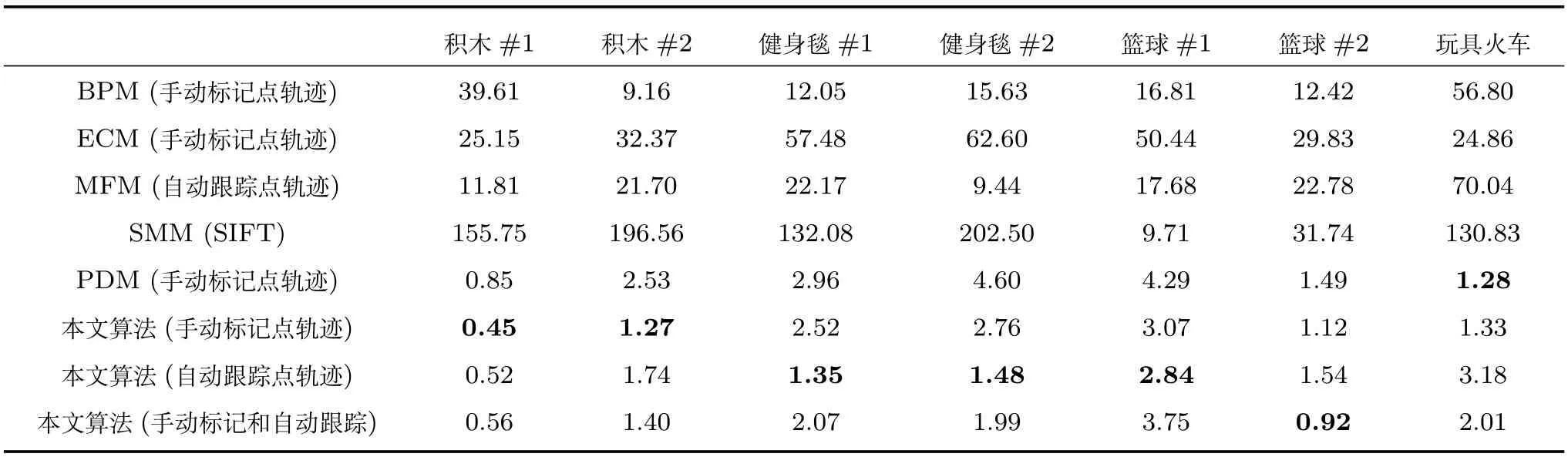
表1 真实数据集上各算法的归一化时域对准误差对比(帧)Table 1 Quantitative comparisons of alignment error on real scenes(frame)

图9 积木场景中各算法的时域对准结果对比(从左到右依次为:参考序列中的图像帧、本文算法、PDM、BPM、ECM、MFM和SMM找到的第二个序列中的对应帧(上)及第三个序列中的对应帧(下))Fig.9 Synchronization results on the blocks scene(From left to right:sample frames from the reference sequence,corresponding frames from the second sequence(top)and the third sequence(bottom)by our method,PDM,BPM,ECM,MFM and SMM,respectively.)

图10 健身毯场景中各算法的时域对准结果对比(同图9)Fig.10 Synchronization results on the exercise mat scene idem as Fig.9

图11 篮球#1场景中各算法的时域对准结果对比(从左到右依次为:参考序列中的图像帧、本文算法、PDM、BPM、ECM、MFM和SMM找到的第二个序列中的对应帧)Fig.11 Synchronization results on the basketball scene(#1)(From left to right:sample frames from the reference sequence,corresponding frames from the second sequence by our method,PDM,BPM,ECM,MFM and SMM,respectively.)

图12 篮球#2场景中各算法的时域对准结果对比(同图11)Fig.12 Synchronization results on the basketball scene(#2)idem as Fig.11

图13 玩具火车场景中各算法的时域对准结果对比(同图11)Fig.13 Synchronization results on the toy train scene idem as Fig.11

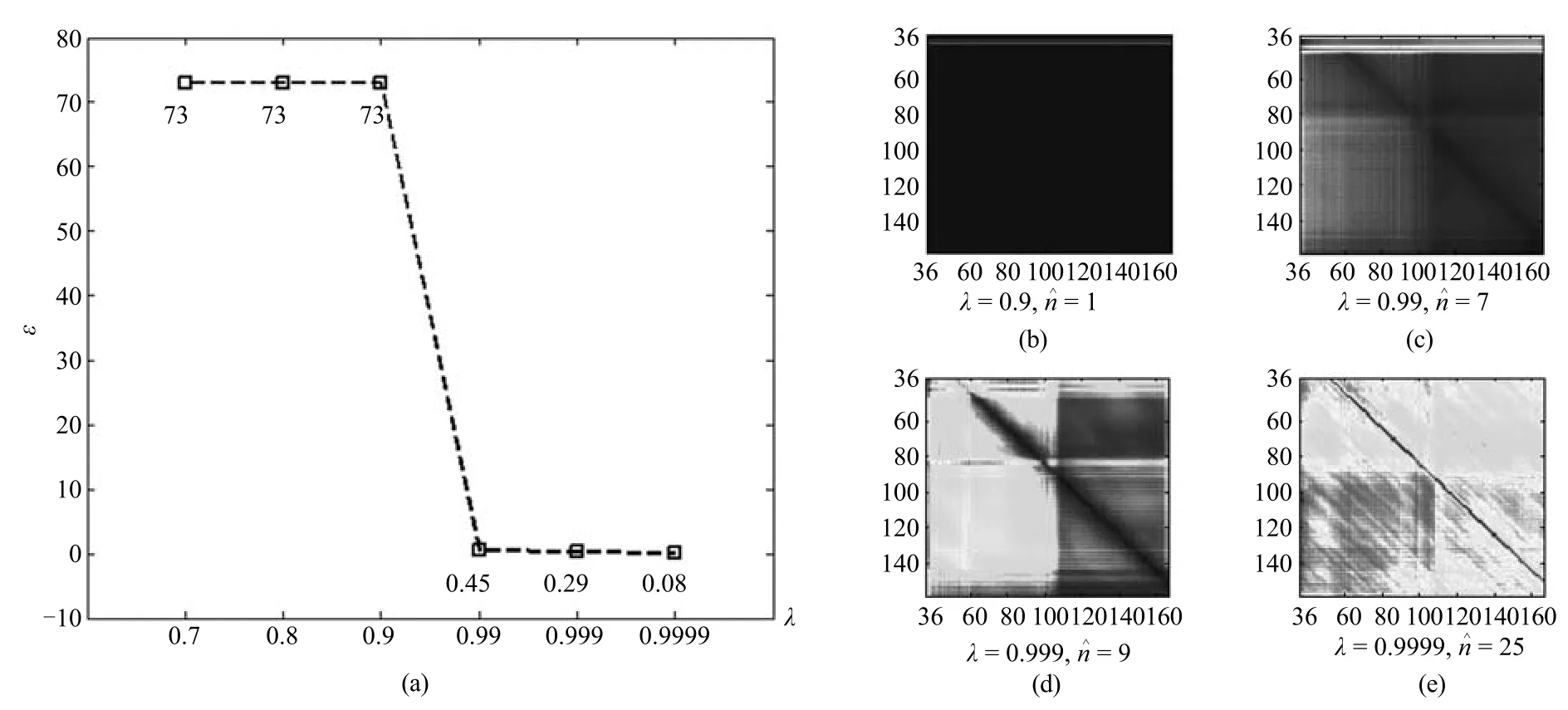
图14 不同有效秩对同步结果的影响及不同有效秩对应的代价矩阵Fig.14 Comparisons of alignment accuracy with different λ values for efficient rank and cost matrices computed with different λ values

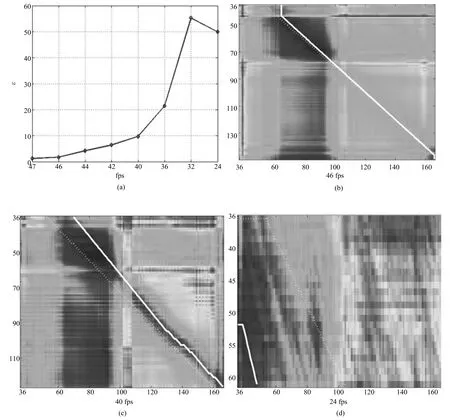
图15 不同帧率比对同步结果的影响及观测序列帧率为46fps、40fps和24fps时的代价矩阵Fig.15 Comparisons of alignment accuracy with different frame rate ratios and cost matrices computed when the frame rate of the observed sequence is 46,40 and 24,respectively

实验选用了如下测试环境:CPU为Inter i5-4570 4-Core 3.20GHz,8GB内存,MATLAB R2010a编程环境.对分辨率为640像素×480像素的一帧图像来说,预处理阶段平均花费时间为204s,其中195s用于图像点轨迹跟踪,6s用于相机空间姿态估计,完整同步算法的平均运行时间为453ms,其中429ms用于三维点轨迹重建.如果序列间点对应关系已知,将算法中基于秩约束的度量准则替换为基于三维重建点距离的度量准则,可以大大提高算法效率,算法平均运行时间缩短到每帧2.8ms.原因在于,对每个空间点,后者仅需要执行一次三维轨迹重建即可,而在基于秩约束的方法中,计算每组子序列对的对齐代价时都要执行一次三维轨迹重建,从而保证参考序列和观测序列具有相同的轨迹基.

5 结论

本文提出一种针对独立运动相机和动态场景的视频时域同步算法.对于给定的轨迹基,利用不同图像序列重建的空间点运动轨迹的系数能够用于同步这些图像序列.我们提出一种基于轨迹基系数的秩约束,结合基于图的最优路径搜索算法,实现视频间的非线性时域对准.本文提出方法不要求图像点轨迹持续整个序列,也不依赖已知的视频间点对应关系,从而能够处理动态场景下由独立运动相机拍摄的视频间的时域同步.

本文方法仅限于若干相机同时拍摄同一场景的情形,类似问题例如人体动作识别或视频检索,是若干相机在不同时刻拍摄相似的场景.本文作者在接下来的工作中会继续研究这类问题的视频同步方法.

1 Caspi Y,Irani M.Spatio-temporal alignment of sequences.IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(11):1409−1424

2 Caspi Y,Simakov D,Irani M.Feature-based sequence-tosequence matching.International Journal of Computer Vision,2006,68(1):53−64

3 Lu C,Mandal M.A robust technique for motion-based video sequences temporal alignment.IEEE Transactions on Multimedia,2013,15(1):70−82

4 Pundik D,Moses Y.Video synchronization using temporal signals from epipolar lines.In:Proceedings of the 11th European Conference on Computer Vision.Heraklion,Crete,Greece:Springer Berlin Heidelberg,2010.15−28

5 P´adua F,Carceroni F,Santos G,Kutulakos K.Linear sequence-to-sequence alignment.IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(2):304−320

6 Yilmaz A,Shah M.Matching actions in presence of camera motion.Computer Vision and Image Understanding,2006,104(2−3):221−231

7 Rao C,Gritai A,Shah M,Syeda-Mahmood T.Viewinvariant alignment and matching of video sequences.In:Proceedings of the 9th IEEE International Conference on Computer Vision.Nice,France:IEEE,2003.939−945

8 Tresadern P A,Reid I D.Video synchronization from human motion using rank constraints.Computer Vision and Image Understanding,2009,113(8):891−906

9 Wolf L,Zomet A.Correspondence-free synchronization and reconstruction in a non-rigid scene.In:Proceedings of the 7th European Conference on Computer Vision,Workshop on Vision and Modelling of Dynamic Scenes.Copenhagen,Denmark:Springer Berlin Heidelberg,2002.

10 Wolf L,Zomet A.Wide baseline matching between unsynchronized video sequences.International Journal of Computer Vision,2006,68(1):43−52

11 Sand P,Teller S.Video matching.ACM Transactions on Graphics,2004,23(3):592−599

12 Evangelidis G D,Bauckhage C.Efficient subframe video alignment using short descriptors.IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(10):2371−2386

13 Serrat J,Diego F,Lumbreras F,´Alvarez J M.Synchronization of video sequences from free-moving camreas.In:Proceedings of the 3rd Iberian Conference on Pattern Recognition and Image Analysis,Part II.Girona,Spain:Springer Berlin Heidelberg,2007.620−627

14 Diego F,Ponsa D,Serrat J,L´opez A M.Video alignment for change detection.IEEE Transactions on Image Processing,2011,20(7):1858−1869

15 Diego F,Serrat J,L´opez A M.Joint spatio-temporal alignment of sequences.IEEE Transactions on Multimedia,2013,15(6):1377−1387

16 Wang O,Schroers C,Zimmer H,Gross M,Sorkine-Hornung A.VideoSnapping:interactive synchronization of multiple videos.ACM Transactions on Graphics,2014,33(4):77:1−77:10

17 Tuytelaars T,van Gool L.Synchronizing video sequences.In:Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington D C,USA:IEEE,2004.762−768

18 Lei C,Yang Y.Trifocal tensor-based multiple video synchronization with subframe optimization.IEEE Transactions on Image Processing,2006,15(9):2473−2480

19 Dexter E,P´erez P,Laptev I.Multi-view synchronization of human actions and dynamic scenes.In:Proceedings of the 2009 British Machine Vision Conference.London,UK:BMVA Press,2009.122:1−122:11

20 Akhter I,Sheikh Y,Khan S,Kanade T.Nonrigid strcture from motion in trajectory space.In:Proceedings of the 2008 Advances in Neural Information Processing Systems.Vancouver,Canada:NIPS,2008.41−48

21 Park H S,Shiratori T,Matthews I,Sheikh Y.3D reconstruction of a moving point from a series of 2D projections.In:Proceedings of the 11th European Conference on Computer Vision.Heraklion,Crete,Greece:Springer,2010.158−171

22 Kutulakos K N,Vallino J.Affine object representations for calibration-free augmented reality.In:Proceedings of the 1996 IEEE Virtual Reality Annual International Symposium.Washington DC,USA:IEEE,1996.25−36

23 Fragkiadaki K,Zhang W J,Zhang G,Shi J B.Twogranularity tracking:mediating trajectory and detection graphs for tracking under occlusions.In:Proceedings of the 12th European Conference on Computer Vision.Florence,Italy:Springer,2012.552−565

24 Lucas B D,Kanade T.An interative image registration technique with an application to stereo vision.In:Proceedings of the 7th International Joint Conference on Arti fi cial Intelligence.Vancouver,Canada:Morgan Kaufmann Publishers Inc.,1981.674−679

25 Snavely N,Seitz S M,Szeliski R.Photo tourism:exploring photo collections in 3D.ACM Transactions on Graphics,2006,25(3):835−846

26 Hartley R I,Zisserman A.Multiple View Geometry in Computer Vision(2nd edition).Cambridge:Cambridge University Press,2004.

27 Park H S,Jain E,Sheikh Y.3D gaze concurrences from head-mounted cameras.In:Proceedings of the 2012 Advances in Neural Information Processing Systems.Nevada,USA:NIPS,2012.422−430